この記事はシリーズ「ソート アルゴリズム」の一部です。
- Selection Sort がどのように動作するかを説明し、
- Selection Sort の Java ソース コードを含み、
- (複雑な数学なしで)その時間複雑性を導き出す方法を示し、Java 実装のパフォーマンスと期待通りの実行時動作が一致するかをチェックするものです。
一連の記事のソース コードは、私の GitHub リポジトリで見つけることができます。 トランプを並べ替える
トランプを手に並べ替えるのは、挿入ソートの典型的な例です。
選択ソートもトランプで説明することができます。 この方法でカードを拾う人を私は知りませんが、例として、かなりうまくいきます;-)
まず、目の前のテーブルにすべてのカードを表向きに並べます。 一番小さいカードを見て、それを手のひらの左側に持っていきます。

- 挿入ソートとの違い
- 選択ソートのアルゴリズム
- ステップ1
- ステップ2
- ステップ 3
- ステップ4
- ステップ5
- ステップ6
- アルゴリズム終了
- 選択ソート Java ソース コード
- Selection Sort Time Complexity
- Runtime of the Java Selection Sort Example
- ワーストケース実行時間の分析
- Analysis of the Runtime for the Search for the Smallest Element
- 選択ソートの他の特徴
- セレクションソートの空間複雑性
- 選択ソートの安定性
- Stable Variant of Selection Sort
- Parallelizability of Selection Sort
- Selection Sort vs. Insertion Sort
- 概要
挿入ソートとの違い
挿入ソートでは、次の未ソートカードを取り出し、ソートされたカードの正しい位置に挿入しました。 未ソートのカードから最小のカードを選択し、それを次々とソート済みのカードに追加していくのです。
選択ソートのアルゴリズム
このアルゴリズムは、例によって最も簡単に説明することができます。 以下のステップでは、選択ソートで配列をソートする方法を示します。
ステップ1
配列を左側のソートされた部分と右側のソートされていない部分に分割します。

ステップ2
右のソートされていない部分で最小の要素を探します。 これを行うには、まず最初の要素である6を記憶します。次のフィールドに移動し、そこでさらに小さな要素である2を見つけます。配列の残りの部分を歩いて、さらに小さな要素を探します。 そして、最初の要素と入れ替えて、正しい位置に配置します。

ステップ 3
右側の未ソート部分を再度検索して、最小の要素を探します。 今度は3です。2番目の位置の要素と交換します:

ステップ4
再び、右側の部分で最小の要素を探します。 それは4であり、すでに正しい位置にある。

ステップ5
最小の要素として、6を見つけます。 これを右側部分の先頭の要素である9:

ステップ6
残りの2要素のうち、7が一番小さくなります。 これを9と入れ替えます。

アルゴリズム終了
最後の要素は自動的に最大となり、したがって正しい位置にあることになります。

選択ソート Java ソース コード
このセクションでは、選択ソートの簡単な Java 実装を見つけることができます。 この要素がソートされると、最後の要素も自動的にソートされる。 ループ変数iは常に右側のソートされていない部分の最初の要素を指す。
各ループサイクルにおいて、右側の部分の最初の要素は最初は最小の要素minとして仮定され、その位置がminPosに格納される。
その後、内側ループは右側部分の2番目の要素からその終わりまで繰り返し、さらに小さい要素が見つかるたびにminとminPosを再割り当てする。
内側ループが完了した後、位置i(右側部分の始まり)とminPosの要素が(それらが同じ要素ではない場合)入れ替わる。
public class SelectionSort { public static void sort(int elements) { int length = elements.length; for (int i = 0; i < length - 1; i++) { // Search the smallest element in the remaining array int minPos = i; int min = elements; for (int j = i + 1; j < length; j++) { if (elements < min) { minPos = j; min = elements; } } // Swap min with element at pos i if (minPos != i) { elements = elements; elements = min; } } }}このコードは GitHub リポジトリの SelectionSort クラスとは異なり、テスト フレームワーク内で簡単に交換できるように SortAlgorithm インターフェイスを実装しています。
Selection Sort Time Complexity
要素の数を n で表し、この例では n = 6 です。
これは明らかに外側のループの場合です:それは n-1 にカウントアップされるのです。
内側のループはどうでしょうか。
次の図を見てください:
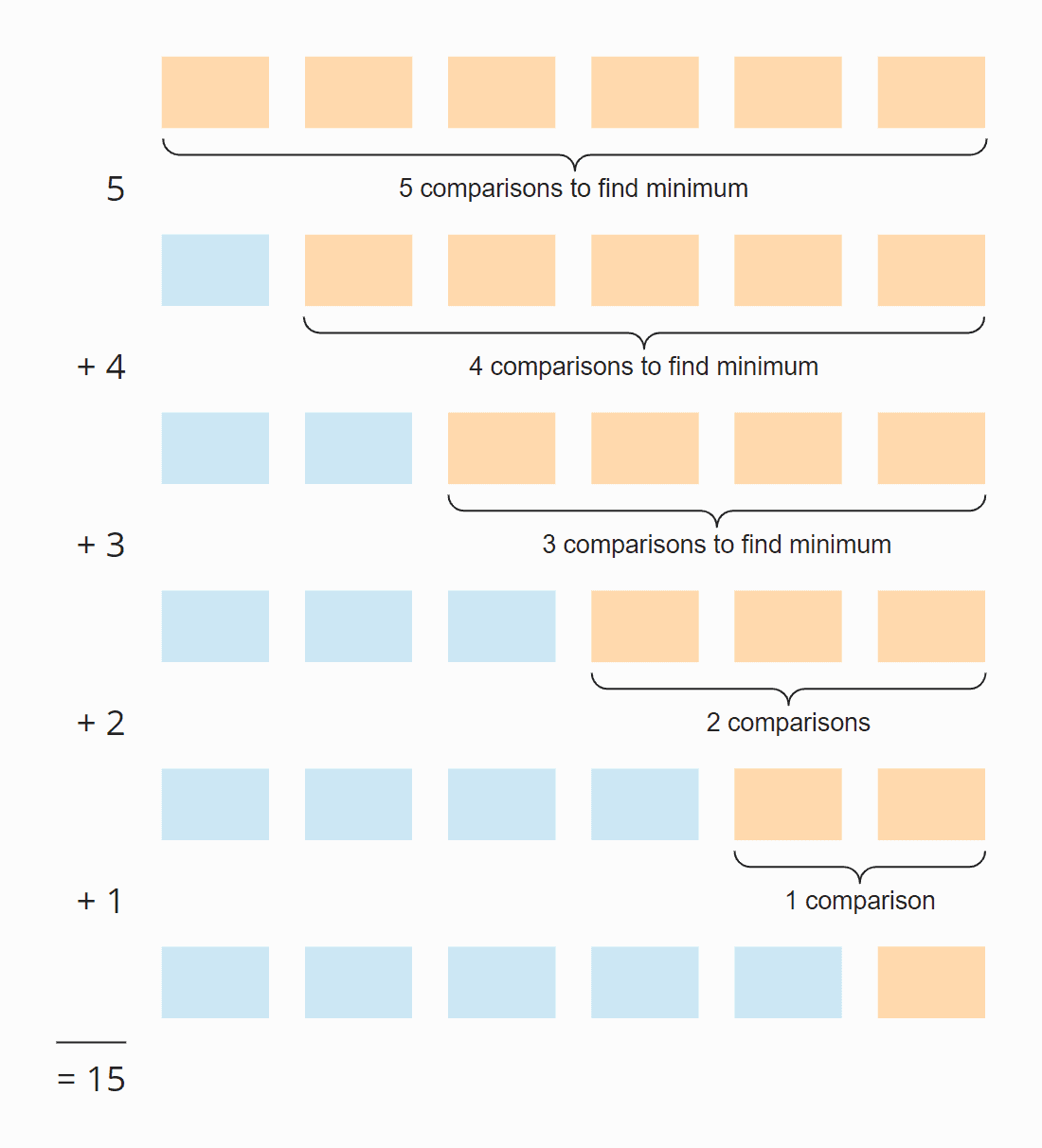
各ステップで、比較の数はソートされていない要素の数より1少ないです。 合計で15回の比較があります – 配列が最初にソートされているかどうかに関係なく。
これは次のように計算することもできます:
要素 6 個×5 ステップ; すべてのステップの平均で、要素の半分がまだソートされていないので、2で割った値です。
6 × 5 × ½ = 30 × ½ = 15
6をnに置き換えると、
n × (n – 1) × ½
乗算すると、
½ n² – ½ n
この項の最大のn乗はn2である。 したがって、最小の要素を探索するための時間複雑度はO(n²)であり、「2次時間」とも呼ばれる。
次に、要素の入れ替えについて見てみよう。 各ステップで(最後のステップを除く)、最小の要素がすでに正しい位置にあるかどうかによって、1つの要素が入れ替わるか、全く入れ替わらないかが決まります。 したがって、合計で最大 n-1 のスワップ操作、すなわち O(n) の時間複雑性、「線形時間」とも呼ばれます。
全体の複雑性については、最高の複雑性クラスのみが問題となるため、
選択ソートの平均、最良の場合、および最悪の場合の時間複雑性は次のようになります。 O(n²)
* 「時間の複雑さ」と「O-notation」という用語は、この記事で例と図を使用して説明します。
Runtime of the Java Selection Sort Example
理論はもう十分です!
- ソートされる要素の数は、最初は1,024要素だったのが反復するたびに2倍になり、536,870,912(=229)要素まで増加します。
- テストが 20 秒以上かかる場合、配列はそれ以上拡張されません。
- すべてのテストは、ソートされていない要素、昇順および降順の事前ソート要素で実行されます。 その後、テストはプロセスが中止されるまで繰り返されます。
各反復の後、プログラムは以前のすべての測定結果の中央値をプリントアウトします。
以下は、50回反復した後の選択ソートの結果です(わかりやすくするために、これは抜粋にすぎません。完全な結果はここにあります):
| n | ソートなし | 上昇 | 降下 | |||
|---|---|---|---|---|---|---|
| …. | … | … | ||||
| 16.384 | 27,9 ms | 26,8 ms | 65,6 ms | |||
| 32.0 ms | … | … | ||||
| … | … | … | … | 108,0 ms | 105,4 ms | 265,4 ms |
| 65.536 | 434,0 ms | 424,3 ms | 1.052,2 ms | |||
| 131.072 | 1.729,8 ms | 1.714,1 ms | 4.209,9 ms | |||
| -262.3 ms | 262.3 ms | 2.3 ms | 1.3 ms | 2.3 ms | ||
| 6.913,4 ms | 6.880,2 ms | 16.863,7 ms | ||||
| 524.288 | 27.649,8 ms | 27.568,7 ms | 67.9 ms | |||
| 67.9ms | 67.9ms |
ここでもう一度、測定値を図にしてみます(ほぼ同じ値のため、「未ソート」と「上昇」を一つの曲線として表示しました)。
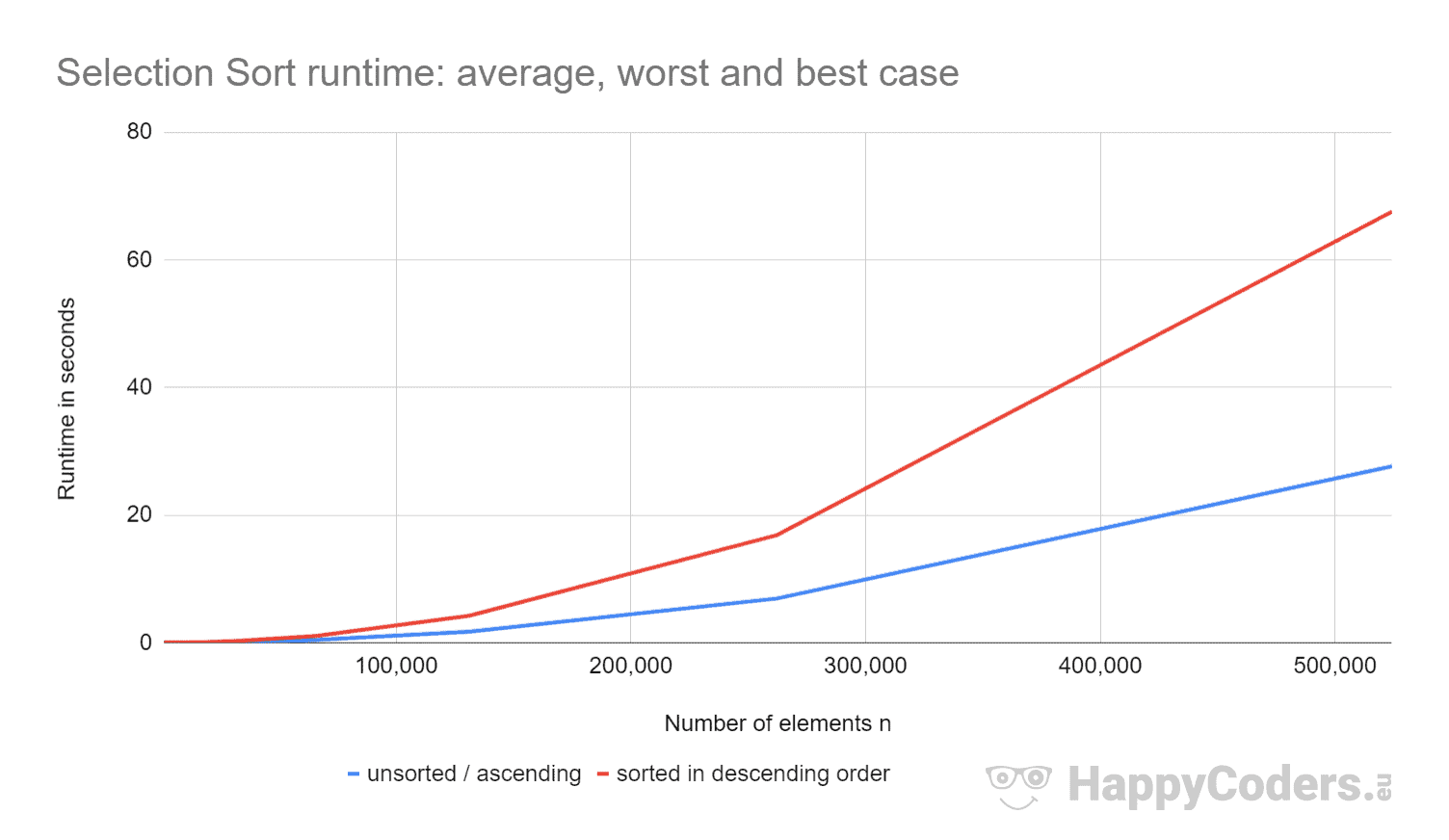
要素の数が2倍になると、要素がソートされているかどうかにかかわらず、実行時間がおよそ4倍になることがわかります。 これはO(n²)の予想される時間複雑性に対応する。
なぜだろうか。
ワーストケース実行時間の分析
理論的には、最小要素の検索は初期状況にかかわらず常に同じ時間を要するはずである。 また、スワップ操作は、降順にソートされた要素についてわずかに多くなるだけのはずです (降順にソートされた要素については、すべての要素をスワップする必要があります。ソートされていない要素については、ほぼすべての要素をスワップする必要があります)。
私の GitHub リポジトリの CountOperations プログラムを使用すると、各種操作数を見ることができます。 ソートされていない要素と降順にソートされた要素の結果を1つの表にまとめてみました。
| n | Comparisons | Swaps unsorted |
Swaps descending |
minPos/min unsorted |
minPos/min descending |
|---|---|---|---|---|---|
| … | … | … | … | … | … |
| 512 | 130.816 | 504 | 256 | 2.866 | 66.047 |
| 1.024 | 523.776 | 1.017 | 512 | 6.439 | 263.167 |
| 2.048 | 2.096.128 | 2.042 | 1.024 | 14.727 | 1.050.623 |
| 4.096 | 8.386.560 | 4.084 | 2.048 | 30.758 | 4.198.399 |
| 8.192 | 33.550.336 | 8.181 | 4.096 | 69.378 | 16.785.407 |
測定値からわかること:
- 降順にソートされた要素では、予想通り、ソートされていない要素と同じくらい、つまりn × (n-1) / 2の比較演算が必要です。
- ソートされていない要素では、想定どおり、要素とほぼ同じ数のスワップ操作があります。たとえば、ソートされていない 4,096 個の要素では、スワップ操作は 4,084 回あります。 これらの数はテストごとにランダムに変わります。
- しかし、要素を降順でソートすると、要素に対して半分のスワップ操作数しかありません! これは、スワップするときに、最も小さい要素を正しい場所に置くだけでなく、それぞれのスワップ相手も置くからです。
たとえば、8つの要素では、スワップ操作は4つです。

さらに、測定結果から、
- 降順に並べられた要素で選択ソートが非常に遅くなる理由は、最小要素を検索する際のローカル変数の割り当て数(
minPosとmin)にあることが分かります。 ソートされていない 8,192 個の要素では、これらの割り当てが 69,378 個あるのに対し、要素が降順にソートされている場合は、その割り当てが 16,785,407 個あり、242 倍になります!
この大きな違いはなぜですか。
Analysis of the Runtime for the Search for the Smallest Element
降順に並べた要素は、上の図から大きさが分かります。 最小の要素を探索するのは、オレンジとオレンジブルーのボックスの三角形に限定される。 上のオレンジ色の部分では、各ボックス内の数字が小さくなり、右のオレンジ色の青色の部分では、数字が再び大きくなっている。
割り当て操作は、各オレンジボックスとオレンジブルーのボックスの1つ目で行われる。 minPos と min の割り当て操作の数は、このように、比喩的に言えば、「2乗の4分の1」程度である。数学的に正確に言えば、¼ n² + n – 1である。
ソートされていない要素については、もっと深く突き詰めなければならないだろう。
したがって、私は、ソートされていない配列の最小の要素を検索するときに、minPos/min 代入がどれだけあるかを測定する小さなデモ プログラムに分析を限定しています。 以下は、100 回反復した後の平均値です (一部抜粋。完全な結果はこちら):
| n | average number of minPos/min assignments |
|---|---|
| 1.1.024 | 7.08 |
| 4.096 | 8.61 |
| 16.385 | 8.94 |
| 65.536 | 11.81 |
| 262.144 | 12.22 |
| 1.048.576 | 14.26 |
| 4.194.304 | 14.71 |
| 16.777.216 | 16.44 |
| 67.108.864 | 17.92 |
| 268.435.456 | 20.27 |
ここで対数X軸の図として:

このグラフから非常にうまく、すなわち対数の成長を持っていることを示しました。 つまり、要素数が 2 倍になるたびに、割り当ての数は一定の値だけ増加します。
このようなminPos/min代入はソートされていない配列ではあまり意味をなさないということです。
選択ソートの他の特徴
以下では、選択ソートの空間複雑性、安定性、並列化可能性を説明しましょう。
セレクションソートの空間複雑性
ループ変数iとj、補助変数length、minPos、min以外に追加のメモリ空間を必要としないので、セレクションソートの空間複雑性は一定である。
つまり、10個でも1000万個でも、どんなに多くの要素をソートしても、必要なのはこの5つの追加変数だけなのである。
選択ソートの安定性
選択ソートは一見して安定しているように見える。 ソートされていない部分が同じキーを持ついくつかの要素を含んでいる場合、最初のものが最初にソートされた部分に追加されるはずである。
しかし外見は欺瞞的である。 なぜなら、アルゴリズムの2番目のサブステップで2つの要素を交換することにより、ソートされていない部分の特定の要素がもはや元の順序を持っていないことが起こり得るからである。 これは、順番に、それらがソートされた部分でもはや元の順序で現れないという事実につながる。
例は非常に簡単に構築することができる。 キーが2の要素とキーが1の要素を以下のように並べ、Selection Sortでソートしたとする:

最初のステップでは、最初と最後の要素が入れ替わっている。 したがって、要素 “TWO” は要素 “two” の後ろになってしまいます。両方の要素の順序が入れ替わります。
第 2 段階では、アルゴリズムは後ろの 2 つの要素を比較します。
第3段階では、1つの要素だけが残り、これは自動的にソートされたとみなされる。
こうして、キー2を持つ2つの要素が最初の順序に入れ替えられ、アルゴリズムが不安定になる。
Stable Variant of Selection Sort
選択ソートは、ステップ 2 で最小の要素と最初の要素を入れ替えず、最初の要素と最小の要素の間のすべての要素を右に 1 位置ずらして、最初の要素に最小の要素を挿入することで安定させることができる。
リンクされたリストでは、ソートされる要素のカットアンドペーストは、大きな性能低下なしに実行できた。
Parallelizability of Selection Sort
外側ループは、反復ごとに配列のコンテンツを変更するので並列化することはできない。
内側のループ(最小要素の探索)は、配列を分割し、各サブ配列の最小要素を並列に探索し、中間結果をマージすれば並列化できます。
Selection Sort vs. Insertion Sort
選択ソートと挿入ソートのどちらが速いか?
私のJava実装の測定結果を比較してみましょう。 Insertion Sort では、最良の場合の時間複雑度は O(n) で、最大 524,288 の要素に対して 1 ミリ秒未満で済みました。 つまり、ベストケースでは、挿入ソートは、任意の要素数で、選択ソートよりも桁違いに高速です。
| n | 選択ソート 未ソート |
挿入ソート 未ソート |
選択ソート 昇順 |
挿入ソート 昇順 |
||
|---|---|---|---|---|---|---|
| … | …. | … | … | |||
| 16.384 | 27,9 ms | 21,9 ms | 65,6 ms | 43,6 ms | ||
| 32.5 ms | 32.6 ms768 | 108,0 ms | 87,9 ms | 265,4 ms | 175,8 ms | |
| 65.536 | 434,0 ms | 350,4 ms | 1.8 ms | 697,6 ms | ||
| 131.072 | 1.729,8 ms | 1.398,9 ms | 4.209,9 ms | 2.840,0 ms | ||
| 262.0 ms | 1.8.144 | 6.913,4 ms | 5.706,8 ms | 16.863,7 ms | 11.517,4 ms | |
| 524.288 | 27.649,8 ms | 23.009,7 ms | 67.1 ms | 4.6 ms | 622.8ms | 622.5ms | 46.309,3 ms |
そしてもう一度図として:

したがって挿入ソートは最良の場合だけではなく平均と最悪の場合でも選択ソートに比べて速くなります。 注意点として、挿入ソートではソートされた要素の半分まで平均して比較とシフトを行うが、選択ソートでは各ステップですべての未ソート要素の中から最小の要素を探す必要がある。
選択ソートは書き込み操作が著しく少ないので、書き込み操作が高価な場合は選択ソートの方が速くなることがある。
実際には、したがって選択ソートはほとんど使用されない。
概要
選択ソートは簡単に実装でき、その典型的な実装では不安定で、平均、最良の場合、および最悪の場合の時間複雑度が O(n²) のソート・アルゴリズムである。
Selection Sort は Insertion Sort よりも遅いため、実際にはほとんど使用されない。
この一連の記事の最初の部分で、すべてのソート アルゴリズムとその特性の概要で、より多くのソート アルゴリズムを見つけることができるだろう。 新しい記事が掲載されたら、メールでお知らせしましょうか?
ニュースレターを購読するには、次のフォームを使用してください。