
植物は、この美しいヒマワリの種の模様のように、螺旋状に新しい細胞を成長させることができます。
「新しい細胞、それからターン、
それから別の細胞、それからターン、…」
How far to turn?
では、もしあなたが植物だとしたら、新しい細胞の間はどのくらい曲がるのでしょうか。
もしまったく曲がらないなら、直線になります。
![]()
しかしそれは非常に貧しい設計です.…隙間なくまとまる丸いものがいいのです。
自分にとっての最適値を探してみてはいかがでしょうか。
0.75, 0.9, 3.1416, 0.62 など、いろいろ試してみてください。
最初から最後まで隙間のないパターンを作ろうとしていることを忘れないでください:
(ちなみに、1.や5などの整数部分は、同じ方向に戻る全回転なので関係ありません。)
What Did You Get?
もしあなたが0.618(または1-0.618の0.382)のように終わるものを得たなら「おめでとう、あなたは植物界の成功者です!」
 |
なぜなら黄金比(1.61803…)が最適解であり、ひまわりはそれを自然な形で発見したのです。 試してみてください…このように見えるはずです。 |
なぜでしょうか?75 は 3/4、0.95 は 19/20 など)、しばらくすると、線が積み重なって隙間ができるパターンになります。
しかし黄金比(その記号はギリシャ文字のファイ、左図)は、どんな分数にもならないエキスパートなのです。
これは無理数(つまり単純な分数として書けない)ですが、それ以上に……どの分数にも近くないということに長けています。
| ただ不合理なだけでは不十分 | |
|---|---|
 |
Pi (3.141592654…) これも不合理であり、不合理な数であると言える。 残念ながら1/7(=0.142857…)に非常に近い小数点を持つので、7腕になってしまいます。 |
 |
e(2.71828….) も不合理ですが、その小数部は 5/7 (0.714285…) に近いので、これも 7 本の腕で終わります。 |
では、黄金比の仕組みは?
| 黄金比の特別な特性の1つは、次のようにそれ自体で定義できることです: | |
| (数字では1.61803・・・= 1 + 1/1.61803….) | |
| これがずっと続く分数に展開できる(「継続分数」と呼ぶ): | |
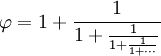 |
|
だから単純分数の合間にきちんと入っているのである。
フィボナッチ数
黄金比とフィボナッチ数(0、1、2、3、5、8、13、21、…など、各数はその前の二つの数の合計)には特別な関係があります。
任意の2つの連続する(1つずつ)フィボナッチ数を取ると、その比率は黄金比に非常に近くなる。
|
a
|
b
|
b / a
|
|
|---|---|---|---|
|
2
|
3
|
1.黄金比は1.5倍、2.0倍、3.0倍となる。5 | |
|
3
|
5
|
1.666666666… | |
|
5
|
8
|
1.6 | |
|
8
|
13
|
1.625 | |
|
13
|
21
|
1.615384615… | |
|
…
|
…
|
… | |
|
144
|
233
|
1.618055556… | |
|
233
|
377
|
1.618025751…. | |
|
…
|
…
|
… |
|

だから0にしたら自然に腕が7本になったのと同じで。142857 (1/7) を使うと、フィボナッチ数が得られるように、黄金比を使うとフィボナッチ数が得られる傾向があります。
試しに、「左回り」の螺旋、そして「右回り」の螺旋・・・と腕を数えてみたら、どんな数字になりましたか?
Spiral Leaf Growth

この興味深い行動は、ひまわりの種に見られるだけではありません。 新しい葉が古い葉からの日差しを遮らないように、あるいは雨や露を最大限に根に導くためです。
実際、植物が螺旋を描くとき、回転はフィボナッチ数で作られた分数になる傾向がある。たとえば、
- 半回転は1/2(1と2はフィボナッチ数)
- 3/5 も普通(両方ともフィボナッチ数)、
- 5/8 も(推測通り!)
- 1/4 もそうだ(推測通り!)。
そして、フィボナッチ数が植物によく見られるのはそのためです。
ここに21枚の花びらを持つヒナギクがあります
(ただし、
いくつかは脱落していたり、ちょうど成長していたりするので、もう少し多いか少ないかを予想してください)
でも、自然にはいろいろな生き残り方法があるので、すべての植物でこれを見るわけではないんですよ。
黄金角
ここまでは「回転」(全回転)の話でした。
0.61803… 回転の相当分は 222.4922… 度、つまり約 222.5 度分です。
反対方向は約137.5°で、「黄金角」と呼ばれています。
今度庭を歩くときは、黄金角を探し、
花びらや葉を数えてフィボナッチ数を見つけ、
植物がいかに賢いかを発見しましょう…!そして、この「黄金角」が、植物がいかに賢いかを発見してください!
エクササイズ
今すぐ庭や公園に行って、葉や花びらを数えたり、回転を測ったりして、何が見つかるか確かめてみましょう。
結果をこの用紙に書いてください:
植物の名前または説明: 葉はらせん状に成長するか? Y / N 葉のグループを数える: 葉はいくつありますか(a)? 一回転(b)何回転しますか(a)? 1葉あたりの回転数 (b/a) :
回転角度 (360 × b/a) :
Are There Flowers? Y / N 花1の花びらの数: 花2:
花 3:
花の数: (ただし、自然には独自のルールがあり、数学的なパターンに従う必要はありませんが、従うとしたら、それは素晴らしいことだと覚えておいてください。
* アニメーションについてのメモ
ひまわりの種は中心から外側に向かって成長しますが、アニメーションでは、若い種を最初に描き、古い種を追加する方が簡単だとわかりました。
スパイラルはプログラムされていません – 正しい回転に保ちながら、種をできるだけ近くに配置しようとした結果、自然に発生します。

