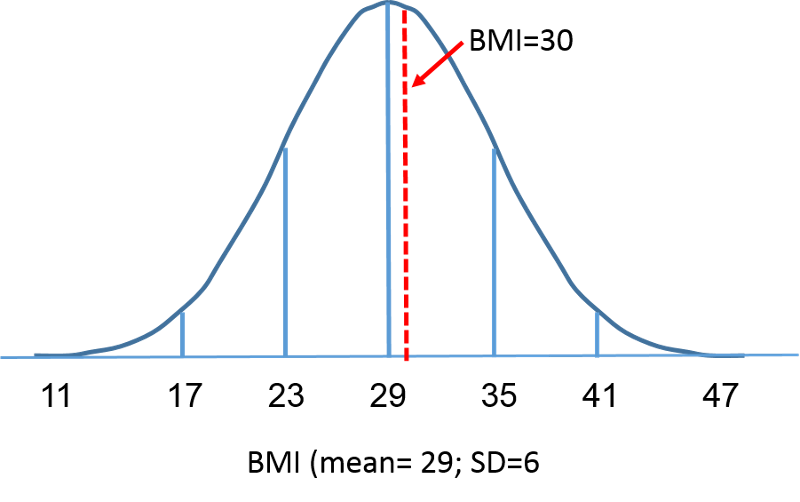
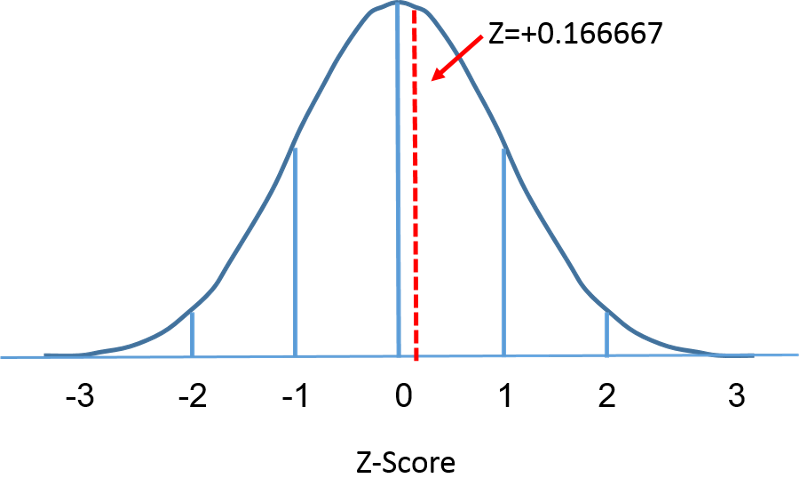
標準正規分布は、平均が0、標準偏差が1の正規分布です。標準正規分布は0を中心とし、ある測定値が平均からどの程度ずれているかは標準偏差で与えられます。 標準正規分布では、観測値の68%が平均から1標準偏差以内に、95%が平均から2標準偏差以内に、99.9%が平均から3標準偏差以内に収まっています。 ここまで、我々は関心のある変数を表すために “X “を使ってきました(例:X=BMI, X=height, X=weight)。 しかし、標準正規分布を使用する場合、我々は、標準正規分布の文脈で変数を参照するために、”Z “を使用することにします。 標準化後、前ページで取り上げたBMI=30は、右の標準正規分布の平均0より0.16667単位高く横たわっていることが下に示されています。
 ====
====
標準曲線下面積=1ですから、特定の観測の確率をより正確に定義し始めてよいのです。 任意のZスコアについて、そのZスコアの左側の曲線の下の面積を計算することができます。 下の枠内の表は、標準正規分布の確率を表しています。 この表を見ると、「Z」スコアが0.0の場合、確率は0.50または50%で、「Z」スコアが1、つまり平均より1標準偏差上の場合、確率は0.8413または84%であることがわかります。 これは、平均値の上下の1つの標準偏差が約68%の面積を占めているので、平均値の上の1つの標準偏差は、その半分の34%を表していることになります。 つまり、平均より下の50%と平均より上の34%を足すと84%になります。
標準正規分布の確率 Z
![]()
この表は、曲線下の面積が指定値または「Z値」よりも左かそれ以下になるように整理したものです。 この場合、平均は0、標準偏差は1ですから、Z値は平均から標準偏差何単位分離れているかを示し、面積はその特定のZ値より小さい値を観測する確率を表しています。 また、この表はZの小数点以下2桁までの確率を示していることに注意してください。単位の場所と小数点以下1桁目は左側の列に、小数点以下2桁目は上の行に渡って表示されています。
しかし、BMIが30未満である確率、すなわちP(X<30)についての質問に戻ろうではありませんか。 この質問には、標準正規分布を使って答えることができます。 下の図は、60歳男性のBMIの分布と標準正規分布を並べたものです。
BMIの分布と標準正規分布
 ====
====
それぞれの曲線下の面積は一つですが、X軸のスケーリングが違います。 ただし、破線の左側の面積は同じであることに注意。 BMIの分布は11から47の範囲で、標準化正規分布のZは-3から3の範囲です。私たちはP(X < 30)を計算したいのです。 これを行うには、X = 30に対応するZ値を決定し、そして、確率または曲線の下の領域を見つけるために、上記の標準正規分布の表を使用することができます。 次の式は、X値をZスコアに変換し、標準化スコアとも呼ばれます:

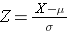
ここでμは変数Xの平均、σは標準偏差です。
P(X < 30)を計算するために、X=30を対応するZスコアに変換します(これを標準化といいます):

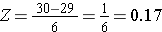
したがって、P(X < 30)= P(Z < 0.17)です。 次に、このZスコアに対応する確率を標準正規分布表から調べると、P(X < 30) = P(Z < 0.17) = 0.5675であることがわかります。
別の例
BMIの同じ分布を使って、60歳の男性のBMIが35を超える確率は何%か。 すなわち、P(X > 35)はいくらか?

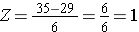
ここで標準正規分布表でP(Z>1)を調べてみると、Z=1.00でP(Z <1.00)=0.8413 となることがわかります。 ただし,この表は常にZが指定値より小さい確率,つまり,P(Z<1)=0.8413を与えることに注意してください。
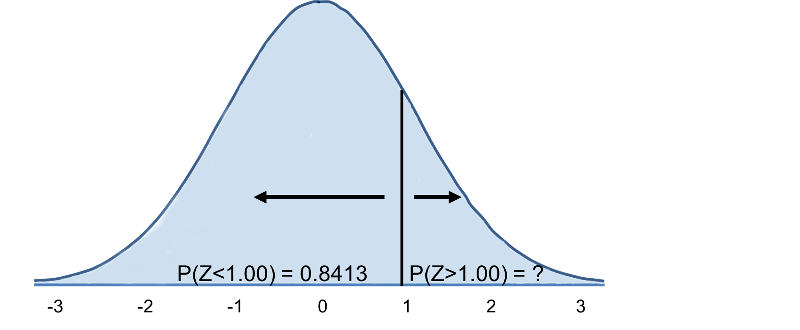
したがって,P(Z>1)=1-0.8413=0.1587です。 解釈
正規確率計算機
![]()
![]()
RによるZスコア
正規確率を表で調べたりエクセルで計算する代わりに、Rで確率を計算することができます。 例えば、
pnorm(0)
Zスコアが0(任意の分布の平均)の場合、左側の面積が50%になる。 上記の母集団の中で60歳の男性がBMI29(平均値)以下である確率はどのくらいでしょうか? Zスコアは0となり、pnorm(0)=0.5または50%となる。
60歳の男性がBMIを30未満とする確率は何%か? Zスコアは0.16667です。
> pnorm(0.16667)
ですから、確率は56.6%です。
60歳の男性がBMI35より大きい確率は?
35-29=6、平均より1標準偏差がありますね。 そこで、左の面積
> pnorm(1)
を計算し、その結果を1.0から引きます。
1-0.8413447= 0.1586553
ですから、60才の高齢者がBMI35以上の確率は15.8%となるのですね。
あるいは、次のようにRを使って全体を一度に計算することもできます:
> 1-pnorm(1)
Probability for a Range of Values

60歳の男性がBMI30~35である確率は何%でしょう。 これは、60歳の男性のうち、BMIが30から35の間にある人の割合はどれくらいか、という質問と同じであることに注意しましょう。 具体的には、P(30 < X < 35)を求めます。 先にP(30<X)とP(X<35)を計算しましたが、この二つの結果を使って、BMIが30と35の間にある確率を計算するにはどうしたらよいでしょうか? 下の説明を見る前に、自分で考えて答えてみてください。
解答
。