- Authenticated encryption with additional data (AEAD) modesEdit
- Galois/counter (GCM)Edit
- Counter with cipher block chaining message authentication code (CCM)Edit
- Synthetic Initialization Vector (SIV) Edit
- AES-GCM-SIVEdit
- Confidentiality only modesEdit
- Electronic codebook (ECB)Edit
- Cipher block chaining (CBC) Edit
- ExampleEdit
- Propagating cipher block chaining (PCBC) Edit
- 暗号フィードバック (CFB)Edit
- Full- (フル)ブロック CFBEdit
- CFB-1, CFB-8, CFB-64, CFB-128, etc.Edit
- CFBと他のモードの比較編集
- Output feedback (OFB)Edit
- Counter (CTR)Edit
Authenticated encryption with additional data (AEAD) modesEdit
1つの暗号プリミティブで秘匿と認証を組み合わせるために、多くの動作モードが設計されています。 その例として、拡張暗号ブロック連鎖(XCBC)、整合性考慮暗号ブロック連鎖(IACBC)、整合性考慮並列化モード(IAPM)、OCB、EAX、CWC、CCM、GCMがある。 認証付き暗号化方式は、シングルパスモードとダブルパスモードに分類される。 OCB モードのようなシングルパス認証暗号化アルゴリズムには、特許に邪魔されるものもありますが、そのような邪魔をしないように特別に設計されてリリースされたものもあります。
さらに、モードによっては、暗号化していない関連データの認証も可能で、これらは AEAD (authenticated encryption with associated data) スキーマと呼ばれます。 例えば、EAXモードはダブルパスのAEAD方式であるのに対し、OCBモードはシングルパスです。
Galois/counter (GCM)Edit
Galois/counter
Yes
Yes
Yes
Galois/counter mode (GCM) はよく知られているカウンターを組み合わせたものです。カウンターモードと呼ばれる暗号化方式と、ガロアモードと呼ばれる新しい認証方式があります。 主な特徴は、認証に使用されるガロア場の乗算の並列計算が容易であることです。 7004>
GCMは、ブロックサイズ128ビットのブロック暗号で定義されています。 Galois メッセージ認証コード (GMAC) は、GCM の認証専用バージョンで、インクリメンタルなメッセージ認証コードを形成することができます。 GCM と GMAC はともに任意の長さの初期化ベクトルを受け入れることができます。 GCM は並列処理の利点を最大限に生かし、GCM の実装では命令パイプラインやハードウ ェアパイプラインを有効に活用することができます。 CTR と同様にブロックに連番を付け、このブロック番号と IV を組み合わせてブロック暗号 E、通常は AES で暗号化します。 この暗号化の結果を平文とXORして、暗号文を生成する。 すべてのカウンターモードと同様に、これは本質的にストリーム暗号であるため、暗号化される各ストリームに異なる IV を使用することが不可欠です。

暗号文ブロックは多項式の係数と考えられ、有限体演算を用いて鍵依存点 H で評価されます。 その結果は暗号化され、データの完全性を確認するために使用できる認証タグが生成される。
Counter with cipher block chaining message authentication code (CCM)Edit
Counter with cipher block chaining message authentication code (counter with CBC-MAC; CCM) は認証と機密性の両方を提供するように設計された認証暗号化アルゴリズムである。 CCMモードはブロック長が128ビットのブロック暗号にのみ定義されている。
Synthetic Initialization Vector (SIV) Edit
SIVは非ce-misuse耐性ブロック暗号モードで、疑似ランダム関数S2Vを用いて内部IVを合成する。 S2VはCMACに基づく鍵付きハッシュであり、関数への入力は次のとおりである:
- 追加認証データ(0、1または多数のAADフィールドがサポートされる)
- 平文
- 認証鍵(K1)。
SIV は、暗号化キー (K2) をキーとして、AES-CTR を使用して S2V 出力と平文を暗号化する。
SIV は外部 nonce ベースの認証暗号化をサポートし、その場合は認証データフィールドをこの目的のために使用することができる。 RFC5297では、相互運用性の観点から、最後の認証済みデータフィールドは外部nonceを使用すべきであると規定されています。
認証キーK1と暗号キーK2の2つのキーを使用するため、SIV AEADバリアントのネーミングスキームはいくつかの混乱を招く可能性があります。
AES-GCM-SIVEdit
AES-GCM-SIV は Advanced Encryption Standard の動作モードで、Galois/counter モードと同様の性能と、暗号 nonce の再利用時の誤用耐性を提供します。 その構成はRFC8452で定義されています。
AES-GCM-SIV は内部IVを合成します。 POLYVALガロアハッシュ関数を用いて、追加認証データと平文のハッシュを導出する。 ハッシュはその後、AES キーで暗号化され、認証タグおよび AES-CTR 初期化ベクトルとして使用されます。 この追加により、GCM-SIV で許可されていた 232 メッセージのみという重大な制限と比較して、同じキーで最大 250 メッセージまで暗号化することができます」
Confidentiality only modesEdit
多くの動作モードが定義されています。 そのうちのいくつかを以下に説明します。 暗号モードの目的は、ECB の弱点の説明で示したように、暗号化データに存在するパターンをマスクすることです。
異なる暗号モードは、暗号ブロックからの出力または他のグローバルに決定可能な変数を後続の暗号ブロックにカスケードすることにより、パターンをマスクします。 リストアップされたモードの入力は次の表にまとめられています。
| モード | 式 | 暗号文 | |||
|---|---|---|---|---|---|
| 電子コードブック | (ECB) | Yi = F(PlainTexti.F) | Electronic Cordbook | Yi = F(PlainTexti, Key) | Yi |
| 暗号ブロック連鎖 | (CBC) | Yi = PlainTexti XOR Ciphertexti-1 | F(Y, Key).Yi | F(Key); Ciphertext0 = IV | |
| Propagating CBC | (PCBC) | Yi = PlainTexti XOR (Ciphertexti-1 XOR PlainTexti-1) | F (Y, Key); Ciphertext0 | F (Y, Key)。 Ciphertext0 = IV | |
| Cipher feedback | (CFB) | Yi = Ciphertexti-1 | Plaintext XOR F(Y, Key).これは、暗号化された平文と平信号の両方を含む。 Ciphertext0 = IV | ||
| 出力フィードバック | (OFB) | Yi = F(Yi-1, Key); Y0 = F(IV, Key) | Plaintext XOR Yi | ||
| Counter | (CTR) | Yi = F(IV + g(i), Key); IV = token() | 平文 XOR Yi | ||
注: g(i)は任意の決定論的関数で、多くの場合、恒等式関数である。
Electronic codebook (ECB)Edit
Electronic codebook
Yes
Yes
Yes
暗号化モードの中で最もシンプルなのがECB(Electronic Codebook)モード(従来の物理コードブックから名付けられた)である。 メッセージはブロックに分割され、各ブロックは別々に暗号化されます。
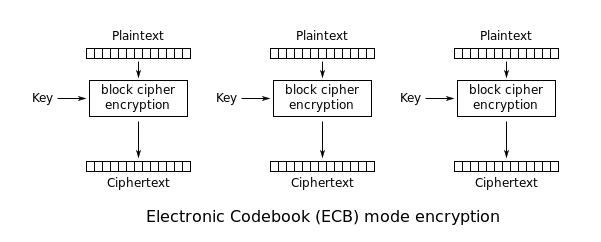

この方法の欠点は、普及が進まないことです。 ECB は同一の平文ブロックを同一の暗号文ブロックに暗号化するため、データ パターンをうまく隠せません。
ECB が平文データ パターンを暗号文にどの程度残すことができるかの顕著な例は、ECB モードが均一色の大きな領域を使用するビットマップ画像の暗号化に使用されたときに見ることができます。 各ピクセルの色は暗号化されますが、オリジナルと同じ色のピクセルのパターンが暗号化されたバージョンに残っているため、画像全体を識別することができます。
ECB モードは、各ブロックがまったく同じ方法で復号されるため、 整合性保護のないプロトコルをリプレイ攻撃に対してより脆弱にすることができます。
Cipher block chaining (CBC) Edit
Cipher block chaining
No
Yes
Yes
Ehrsam, Meyer、Smith、Tuchmanの4人は、1976年にCBC(cipher block chaining)動作モードを発明しました。 CBCモードでは、平文の各ブロックは暗号化される前に前の暗号文のブロックとXORされます。 このようにして、各暗号文ブロックは、その時点までに処理されたすべての平文ブロックに依存する。 各メッセージを一意にするために、最初のブロックに初期化ベクトルを使用しなければならない。
最初のブロックがインデックス1の場合、CBC暗号化の数式は
C i = E K ( P i ⊕ C i – 1 ) , {displaystyle C_{i}=E_{K}(P_{i}oplus C_{i-1}),}

C 0 = I V , {displaystyle C_{0}=IV,}

一方、CBC復号の数式は
P i = D K ( C i ) ⊕ C i – 1 , {displaystyle P_{i}=D_{K}(C_{i})\oplus C_{i-1}, }

C 0=I V . {displaystyle C_{0}=IV.}.

ExampleEdit
CBC は最もよく使われる操作モードである。 その主な欠点は、暗号化がシーケンシャルであること(つまり、並列化できないこと)と、メッセージが暗号ブロック・サイズの倍数になるようにパディングされなければならないことです。 この最後の問題を処理する一つの方法は、暗号文の盗み見として知られる方法です。 平文または初期化ベクトル (IV) の 1 ビットの変更は、それに続くすべての暗号文ブロックに影響することに注意してください。
不正な IV で復号すると、平文の最初のブロックは破損しますが、その後の平文ブロックは正しくなります。 これは、各ブロックが平文ではなく、前のブロックの暗号文と XOR されるためで、現在のブロックの復号化の IV として使用する前に、前のブロックを復号化する必要はないのです。 つまり、隣接する2つの暗号文ブロックから平文ブロックを復元することができるのです。 その結果、復号化の並列化が可能になります。 暗号文に1ビットの変更を加えると、対応する平文ブロックが完全に破壊され、次の平文ブロックの対応するビットが反転するが、残りのブロックは無傷のままであることに注意されたい。 この特性は、POODLE などのさまざまなパディングオラクル攻撃に利用されます。
Explicit initialization vectors は、平文に 1 つのランダムブロックを前置することでこの特性を利用します。 暗号化は、IV が復号化ルーチンに伝達される必要がないことを除いて、通常通り行われます。 復号化で使用するIVが何であれ、ランダムブロックだけが「破壊」される。 これは安全に捨てることができ、復号化の残りは元の平文となる。
Propagating cipher block chaining (PCBC) Edit
Propagating cipher block chaining
No
No
No
普及型暗号ブロックチェイニングまたは平文暗号ブロックチェイニングは、暗号の解読と復号化を同時に行うことができます。ブロック連鎖モードは、復号化する際に暗号文の小さな変化が無限に伝播するように設計されています。 暗号化するときと同じように PCBCモードでは、平文の各ブロックは、暗号化される前に、前の平文ブロックおよび前の暗号文ブロックの両方とXORされます。 CBC モードと同様に、最初のブロックに初期化ベクトルが使用される。
暗号化・復号化のアルゴリズムは以下の通りです。
C i = E K ( P i ⊕ P i – 1 ⊕ C i – 1 ) , P 0 ⊕ C 0 = I V , {displaystyle C_{i}=E_{K}(P_{i}oplus P_{i-1}oplus C_{i-1})=I_{K},P_{0} Θ C_{0}=IV,}

P i = D K ( C i ) ⊕ P i – 1 ⊕ C i – 1 , P 0 ⊕ C 0 = I V . P_{i}=D_{K}(C_{i})ゞ P_{i-1} plus C_{i-1},P_{0} plus C_{0}=IV.} {displaystyle P_{i}=D_{K}(C_{i})ゞ } ゞ

PCBC は特に Kerberos v4 と WASTE で使用されていますが、それ以外では一般的ではありません。 PCBC モードで暗号化されたメッセージでは、2 つの隣接する暗号文ブロックが交換されても、それ以降のブロックの復号化には影響しません。 このため、PCBCはKerberos v5では使用されていない。
暗号フィードバック (CFB)Edit
Full- (フル)ブロック CFBEdit
Cipher feedback
No
Yes
Yes
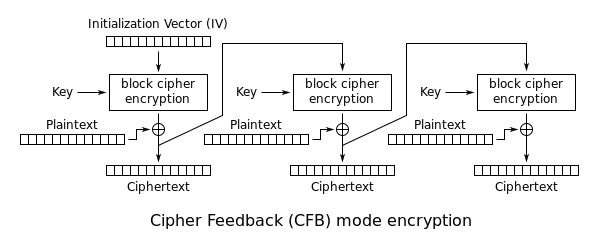
Cipher feedback (CFB) モードのこと。 は、ブロック暗号の出力全体を使用する最も単純な形態である。 このバリエーションでは、CBCと非常によく似ており、ブロック暗号を自己同期型ストリーム暗号にします。 このバリエーションにおけるCFB復号は、CBC暗号を逆にしたものとほぼ同じである。
C i = { IV , i = 0 E K ( C i – 1 ) ⊕ P i , otherwise P i = E K ( C i – 1 ) ⊕ C i , {displaystyle {begin{aligned}C_{i}&={}begin{cases}{text{IV}}.{}} {Description {C_Description {C_Description {C_Description {C_Description {C_Description {C_Description {C_Description {C_Description {C_Description {C_Description {C_Description&i=0\\E_{K}(C_{i-1})\oplus P_{i},&{\text{otherwise}}\end{cases}}\\P_{i}&=E_{K}(C_{i-1})\oplus C_{i},\end{aligned}}}


CFB-1, CFB-8, CFB-64, CFB-128, etc.Edit
NIST SP800-38Aではビット幅でCFBが定義されています。 また、CFBモードでは、1≦s≦bとなるようなsと表記される整数のパラメータを必要とする。以下のCFBモードの仕様では、平文セグメント(Pj)および暗号文セグメント(Cj)はそれぞれsビットで構成されている。 sの値は、1ビットCFBモード、8ビットCFBモード、64ビットCFBモード、128ビットCFBモードなどのように、モードの名前に組み込まれることもある。
これらのモードは、基礎となるブロック暗号の出力を切り捨てる。
I 0 = IV . {\displaystyle I_{0}={\text{IV}}.}

I i = ( ( I i – 1 ≪ s ) + C i ) mod 2 b , {displaystyle I_{i}={big (}(I_{i-1}ll s)+C_{i}{big )}{bmod {2}}^{b},}

C i = MSB s ( E K ( I i – 1 ) ) ⊕ P i , {Displaystyle C_{i}= Operatorname {MSB} } }. _{s}{Thomasbig (}E_{K}(I_{i-1}){Thomasbig )}}oplus P_{i},}

P i = MSB s ( E K ( I i – 1 ) )である。 ⊕ C i , {displaystyle P_{i}= Cabinet Operatorname {MSB}. _{s}{Copyright (}E_{K}(I_{i-1}){}big )}}oplus C_{i},}

CFB-1 は自己同期で暗号文の消失に強いとされており、「1ビットCFBモードでは挿入または削除ビット後b+1ポジションで自動的に同期が復元される」。 CFBモードのsの他の値、およびこの勧告の他の機密性モードでは、同期は外部から復元されなければならない。” (NIST SP800-38A)。 AESのような128ビット幅のブロック暗号で1ビット損失すると、有効なビットを出す前に129の無効なビットを出します。
CFB は、指定した以外の特別な場合にも自己同期を行うことがあります。 例えば、128ビットブロック暗号のCFB-128で1ビット変更すると、2ブロック後に再同期されます。 (ただし、CFB-128などはビット損失を優雅に扱わない。1ビット損失は、復号器が暗号器との整合を失う原因となる)
CFBと他のモードの比較編集
CBCモードのように、平文の変更は暗号文に永遠に伝播し、暗号化を並列化することができない。 ブロック暗号は暗号化方向でのみ使用され、メッセージは暗号ブロックサイズの倍数になるようにパディングする必要がありません(ただし、パディングを不要にするためにCBCモードで暗号文の盗用を使用することも可能です)。
Output feedback (OFB)Edit
Output feedback
No
No
No
出力フィードバック(OSB)モードはブロック暗号を同期型ストリーム暗号にするモードである。 鍵ストリームブロックを生成し、それを平文ブロックとXORして暗号文を得る。 他のストリーム暗号と同様に、暗号文のビットを反転させると、平文でも同じ位置で反転したビットが生成される。 この性質により、多くの誤り訂正符号が暗号化前に適用されても正常に機能する。
XOR演算の対称性から、暗号化と復号は全く同じになる。
C j = P j ⊕ O j , {}displaystyle C_{j}=P_{j}oplus O_{j},}

P j = C j ⊕ O j , {displaystyle P_{j}=C_{j}oplus O_{j}.{}
C j ⊖ O j , {}Displaystyle C_{j}=P_{j} Plus O_{j},}

O j = E K ( I j ),{\displaystyle O_{j}=E_{K}(I_{j}),}

I j = O j – 1 , {\displaystyle I_{j}=O_{j-1},}

I 0 = IV . {\displaystyle I_{0}={\text{IV}}.}


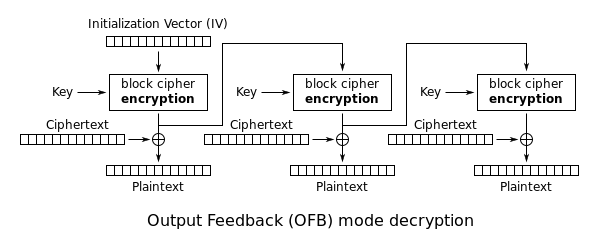
各出力フィードバックブロック暗号演算は以前のすべてのものに依存するので、並行して実行することはできない。 しかし、平文または暗号文は最後の XOR にのみ使用されるため、ブロック暗号演算を事前に実行することができ、平文または暗号文が利用可能になった時点で最終ステップを並行して実行することが可能です。 これは、CBCモードの高速ハードウェア実装をOFBモードの暗号化に使用できるため、有用である。
CFBモードのように部分ブロックをフィードバックとしてOFBモードを使用すると、平均サイクル長が232倍以上短縮される。 DaviesとParkinによって提案され、実験結果によって実証された数学的モデルは、完全なフィードバックにおいてのみ、得られる最大値に近い平均サイクル長が達成できることを示しました。 このため、OFBの仕様から切り捨てられたフィードバックのサポートが削除された。
Counter (CTR)Edit
Counter
Yes
Yes
Yes
注意事項。 CTRモード(CM)は、整数カウンタモード(ICM)、セグメント化整数カウンタ(SIC)モードとしても知られています。
OFBと同様に、カウンターモードはブロック暗号をストリーム暗号に変えます。 これは、「カウンタ」の連続する値を暗号化して次の鍵ストリームブロックを生成する。 カウンタには、長期間繰り返さないことが保証されるシーケンスを生成する関数であれば何でもかまいませんが、実際の1秒刻みのカウンタが最も単純でよく使われています。 批評家は「既知の系統的な入力に暗号システムを意図的にさらすことは、不必要なリスクを意味する」と主張した。 しかし、今日ではCTRモードは広く受け入れられており、いかなる問題も基礎となるブロック暗号の弱点とみなされ、入力の系統的な偏りに関係なく安全であることが期待されています。 CBC とともに、CTR モードは Niels Ferguson と Bruce Schneier が推奨する 2 つのブロック暗号モードの 1 つです。
CTR モードは 1979 年に Whitfield Diffie と Martin Hellman によって導入されました。CTR モードは OFB と同様の特性を持っていますが、復号時にランダム アクセスの特性も許容しています。 CTRモードは、ブロックを並行して暗号化できるマルチプロセッサ・マシンでの動作に適している。 さらに、OFB に影響を与える可能性のあるショートサイクルの問題もありません。
IV/nonce がランダムである場合、任意の反転演算(連結、加算、XOR)を使用して、カウンターと一緒に組み合わせ、暗号化用の実際の固有のカウンターブロックを生成することが可能です。 非ランダムな nonce(パケットカウンタなど)の場合、nonce とカウンタは連結されるべきである(例えば、128 ビットのカウンタブロックの上位 64 ビットに nonce を、下位 64 ビットにカウンタを格納する)。 nonce とカウンタを単純に加算または XOR して一つの値にすると、攻撃者が IV とカウンタのペア全体を操作して衝突を引き起こすことができるため、多くの場合選択平文攻撃によるセキュリティが破られることになる。 攻撃者が IV カウンターペアと平文を制御すると、暗号文と既知の平文の XOR は、同じ IV カウンターペアを共有する他のブロックの暗号文と XOR したとき、そのブロックを復号する値を生成します。 しかし、オフセット/位置情報が破損している場合、バイトオフセットに依存するため、そのようなデータを部分的に回復することは不可能になります。