Questo articolo fa parte della serie “Algoritmi di ordinamento: Ultimate Guide” e…
- descrive come funziona Selection Sort,
- include il codice sorgente Java per Selection Sort,
- mostra come ricavare la sua complessità temporale (senza complicati calcoli matematici)
- e controlla se la performance dell’implementazione Java corrisponde al comportamento runtime previsto.
Puoi trovare il codice sorgente dell’intera serie di articoli nel mio repository GitHub.
- Esempio: Ordinamento delle carte da gioco
- Differenza da Insertion Sort
- Algoritmo di selezione
- Passo 1
- Passo 2
- Passo 3
- Passo 4
- Passo 5
- Passo 6
- Algoritmo finito
- Selection Sort Java Source Code
- Complessità temporale di Selection Sort
- Runtime dell’esempio Java Selection Sort
- Analisi del runtime del caso peggiore
- Analisi del tempo di esecuzione della ricerca dell’elemento più piccolo
- Altre caratteristiche di Selection Sort
- Complessità dello spazio di Selection Sort
- Stabilità di Selection Sort
- Variante stabile di Selection Sort
- Parallelizzabilità di Selection Sort
- Selection Sort vs. Insertion Sort
- Sommario
Esempio: Ordinamento delle carte da gioco
L’ordinamento delle carte da gioco nella mano è il classico esempio di ordinamento a inserimento.
Anche l’ordinamento a selezione può essere illustrato con le carte da gioco. Non conosco nessuno che raccoglie le sue carte in questo modo, ma come esempio, funziona abbastanza bene 😉
Primo, metti tutte le tue carte a faccia in su sul tavolo di fronte a te. Cerchi la carta più piccola e la porti a sinistra della tua mano. Poi cerchi la prossima carta più grande e la metti alla destra della carta più piccola, e così via fino a quando finalmente prendi la carta più grande all’estrema destra.

Differenza da Insertion Sort
Con Insertion Sort, abbiamo preso la prossima carta non ordinata e l’abbiamo inserita nella giusta posizione nelle carte ordinate.
Selection Sort funziona più o meno al contrario: Selezioniamo la carta più piccola tra le carte non ordinate e poi – una dopo l’altra – la aggiungiamo alle carte già ordinate.
Algoritmo di selezione
L’algoritmo può essere spiegato più semplicemente con un esempio. Nei seguenti passi, mostro come ordinare l’array con Selection Sort:
Passo 1
Dividiamo l’array in una parte sinistra, ordinata, e una parte destra, non ordinata. La parte ordinata è vuota all’inizio:

Passo 2
Cerchiamo l’elemento più piccolo nella parte destra, non ordinata. Per fare questo, ricordiamo prima il primo elemento, che è il 6. Andiamo al campo successivo, dove troviamo un elemento ancora più piccolo nel 2. Percorriamo il resto della matrice, cercando un elemento ancora più piccolo. Dato che non ne troviamo uno, rimaniamo con il 2. Lo mettiamo nella posizione corretta scambiandolo con l’elemento al primo posto. Poi spostiamo il confine tra le sezioni dell’array un campo a destra:

Passo 3
Ricerchiamo nella parte destra, non ordinata, l’elemento più piccolo. Questa volta è il 3; lo scambiamo con l’elemento in seconda posizione:

Passo 4
Di nuovo cerchiamo l’elemento più piccolo nella parte destra. È il 4, che è già nella posizione corretta. Quindi non c’è bisogno dell’operazione di scambio in questo passo, e spostiamo solo il bordo della sezione:

Passo 5
Come elemento più piccolo, troviamo il 6. Lo scambiamo con l’elemento all’inizio della parte destra, il 9:

Passo 6
Degli altri due elementi, il 7 è il più piccolo. Lo scambiamo con il 9:

Algoritmo finito
L’ultimo elemento è automaticamente il più grande e, quindi, nella posizione corretta. L’algoritmo è finito, e gli elementi sono ordinati:

Selection Sort Java Source Code
In questa sezione, troverete una semplice implementazione Java di Selection Sort.
Il ciclo esterno itera sugli elementi da ordinare, e finisce dopo il penultimo elemento. Quando questo elemento viene ordinato, anche l’ultimo elemento viene automaticamente ordinato. La variabile del ciclo i punta sempre al primo elemento della parte destra, non ordinata.
In ogni ciclo del ciclo, il primo elemento della parte destra è inizialmente assunto come l’elemento più piccolo min; la sua posizione è memorizzata in minPos.
Il ciclo interno itera poi dal secondo elemento della parte destra fino alla sua fine e riassegna min e minPos ogni volta che viene trovato un elemento ancora più piccolo.
Dopo che il ciclo interno è stato completato, gli elementi delle posizioni i (inizio della parte destra) e minPos sono scambiati (a meno che non siano lo stesso elemento).
public class SelectionSort { public static void sort(int elements) { int length = elements.length; for (int i = 0; i < length - 1; i++) { // Search the smallest element in the remaining array int minPos = i; int min = elements; for (int j = i + 1; j < length; j++) { if (elements < min) { minPos = j; min = elements; } } // Swap min with element at pos i if (minPos != i) { elements = elements; elements = min; } } }}Il codice mostrato differisce dalla classe SelectionSort nel repository GitHub in quanto implementa l’interfaccia SortAlgorithm per essere facilmente intercambiabile all’interno del framework di test.
Complessità temporale di Selection Sort
Denominiamo con n il numero di elementi, nel nostro esempio n = 6.
I due loop annidati indicano che abbiamo a che fare con una complessità temporale* di O(n²). Questo sarà il caso se entrambi i cicli iterano ad un valore che aumenta linearmente con n.
È ovviamente il caso del ciclo esterno: conta fino a n-1.
Che dire del ciclo interno?
Guardate la seguente illustrazione:
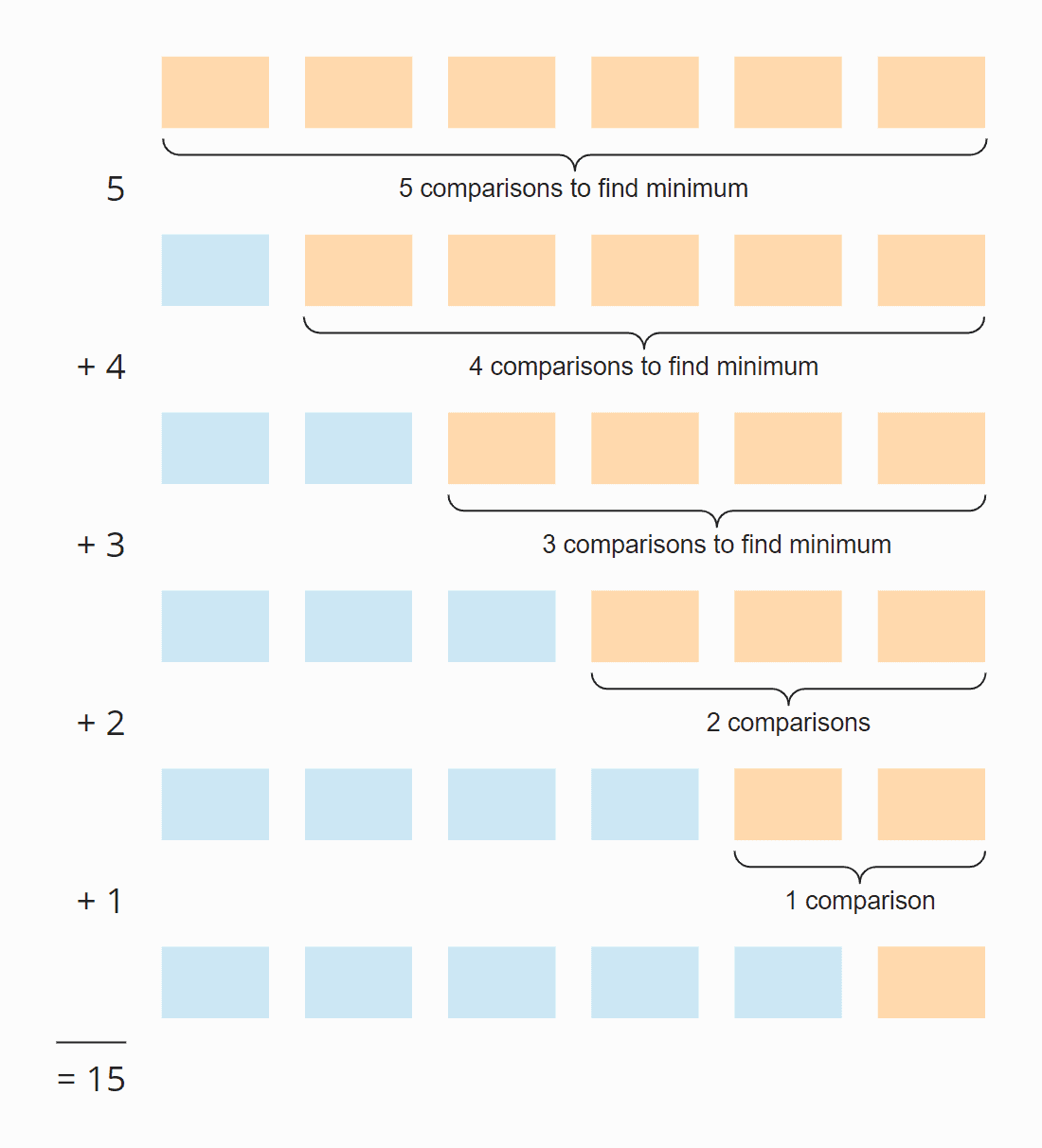
In ogni passo, il numero di confronti è uno meno del numero di elementi non ordinati. In totale, ci sono 15 confronti – indipendentemente dal fatto che l’array sia inizialmente ordinato o meno.
Questo può anche essere calcolato come segue:
Sei elementi per cinque passi; diviso per due, poiché in media su tutti i passi, metà degli elementi sono ancora non ordinati:
6 × 5 × ½ = 30 × ½ = 15
Se sostituiamo 6 con n, otteniamo
n × (n – 1) × ½
Moltiplicato, è:
½ n² – ½ n
La massima potenza di n in questo termine è n². La complessità temporale per la ricerca dell’elemento più piccolo è, quindi, O(n²) – chiamato anche “tempo quadratico”.
Guardiamo ora lo scambio degli elementi. In ogni passo (tranne l’ultimo), viene scambiato un elemento o nessuno, a seconda che l’elemento più piccolo sia già nella posizione corretta o meno. Così, abbiamo, in somma, un massimo di n-1 operazioni di scambio, cioè, la complessità temporale di O(n) – chiamata anche “tempo lineare”.
Per la complessità totale, solo la classe di complessità più alta conta, quindi:
La complessità temporale media, best-case, e worst-case di Selection Sort è: O(n²)
* I termini “complessità temporale” e “O-notazione” sono spiegati in questo articolo usando esempi e diagrammi.
Runtime dell’esempio Java Selection Sort
Basta teoria! Ho scritto un programma di test che misura il tempo di esecuzione di Selection Sort (e di tutti gli altri algoritmi di ordinamento trattati in questa serie) come segue:
- Il numero di elementi da ordinare raddoppia dopo ogni iterazione da inizialmente 1.024 elementi fino a 536.870.912 (= 229) elementi. Un array di due volte questa dimensione non può essere creato in Java.
- Se un test dura più di 20 secondi, l’array non viene esteso ulteriormente.
- Tutti i test vengono eseguiti con elementi non ordinati e con elementi pre-ordinati ascendenti e discendenti.
- Abbiamo permesso al compilatore HotSpot di ottimizzare il codice con due cicli di riscaldamento. Dopo di che, i test vengono ripetuti fino a quando il processo viene interrotto.
Dopo ogni iterazione, il programma stampa la mediana di tutti i risultati delle misure precedenti.
Ecco il risultato per Selection Sort dopo 50 iterazioni (per chiarezza, questo è solo un estratto; il risultato completo può essere trovato qui):
| n | non ordinata | ascendente | discendente |
|---|---|---|---|
| … | … | … | … |
| 16.384 | 27,9 ms | 26,8 ms | 65,6 ms |
| 32.768 | 108,0 ms | 105,4 ms | 265,4 ms |
| 65.536 | 434,0 ms | 424,3 ms | 1.052,2 ms |
| 131.072 | 1.729,8 ms | 1.714,1 ms | 4.209,9 ms |
| 262.144 | 6.913,4 ms | 6.880,2 ms | 16.863,7 ms |
| 524.288 | 27.649,8 ms | 27.568,7 ms | 67.537,8 ms |
Qui le misure ancora una volta come un diagramma (dove ho visualizzato “non ordinate” e “ascendenti” come una sola curva a causa dei valori quasi identici):
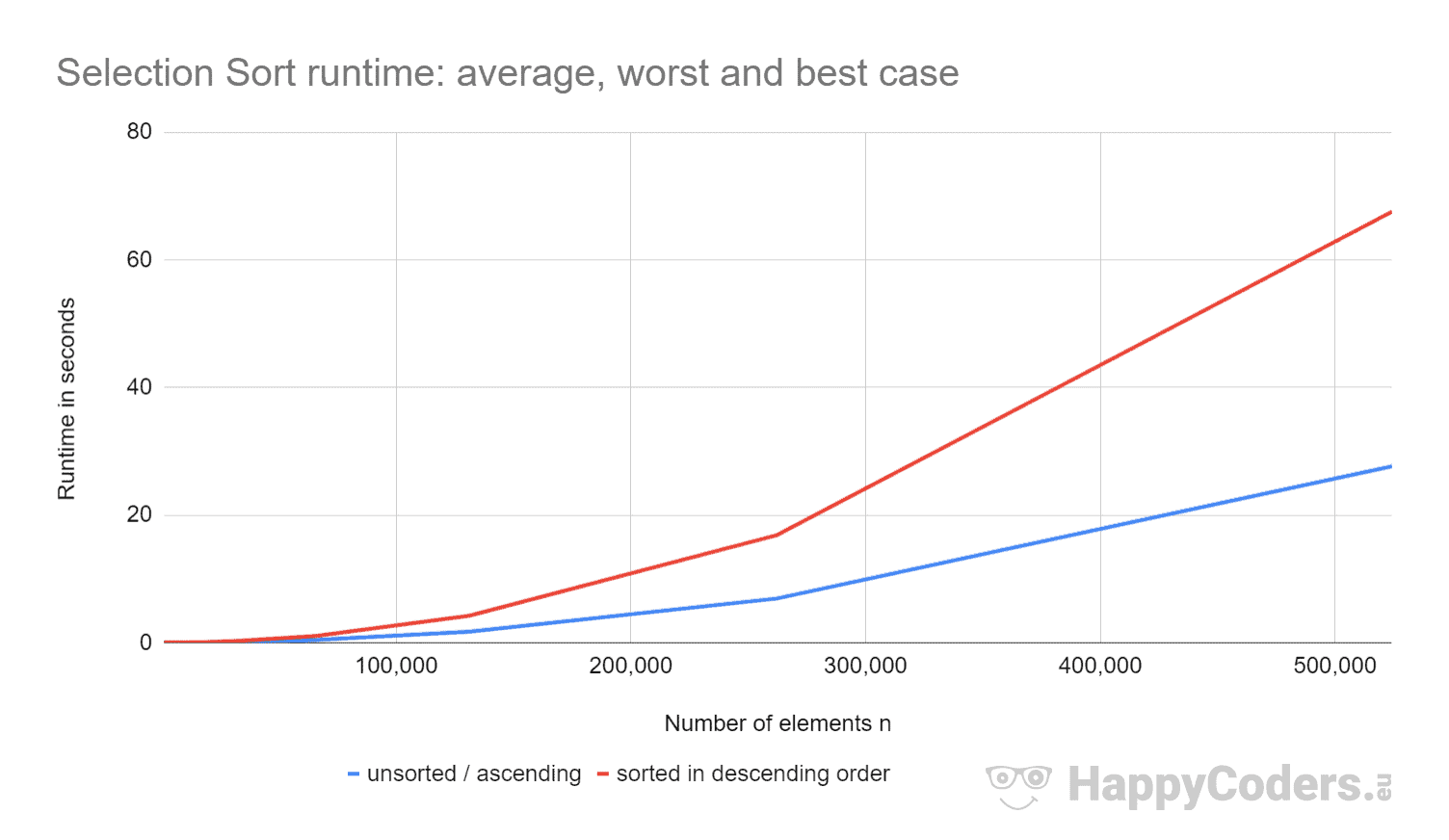
È bello vedere che
- se il numero di elementi è raddoppiato, il tempo di esecuzione è circa quadruplicato – indipendentemente dal fatto che gli elementi siano precedentemente ordinati o meno. Questo corrisponde alla complessità temporale prevista di O(n²).
- che il tempo di esecuzione per elementi ordinati ascendenti è leggermente migliore che per elementi non ordinati. Questo perché le operazioni di swapping, che – come analizzato sopra – sono di poca importanza, qui non sono necessarie.
- che il runtime per gli elementi ordinati discendenti è significativamente peggiore di quello per gli elementi non ordinati.
Perché?
Analisi del runtime del caso peggiore
In teoria, la ricerca dell’elemento più piccolo dovrebbe richiedere sempre la stessa quantità di tempo, indipendentemente dalla situazione iniziale. E le operazioni di swap dovrebbero essere solo leggermente superiori per gli elementi ordinati in ordine decrescente (per gli elementi ordinati in ordine decrescente, ogni elemento dovrebbe essere scambiato; per gli elementi non ordinati, quasi ogni elemento dovrebbe essere scambiato).
Utilizzando il programma CountOperations dal mio repository GitHub, possiamo vedere il numero delle varie operazioni. Ecco i risultati per elementi non ordinati ed elementi ordinati in ordine decrescente, riassunti in una tabella:
| n | Confronti | Swaps unsorted |
Swaps descending |
minPos/min non ordinati |
minPos/min discendenti |
|---|---|---|---|---|---|
| … | … | … | … | … | … |
| 512 | 130.816 | 504 | 256 | 2.866 | 66.047 |
| 1.024 | 523.776 | 1.017 | 512 | 6.439 | 263.167 |
| 2.048 | 2.096.128 | 2.042 | 1.024 | 14.727 | 1.050.623 |
| 4.096 | 8.386.560 | 4.084 | 2.048 | 30.758 | 4.198.399 |
| 8.192 | 33.550.336 | 8.181 | 4.096 | 69.378 | 16.785.407 |
Dai valori misurati si può vedere:
- Con elementi ordinati in ordine decrescente, abbiamo – come previsto – tante operazioni di confronto quante con elementi non ordinati – cioè n × (n-1) / 2.
- Con elementi non ordinati, abbiamo – come previsto – quasi tante operazioni di scambio quanti sono gli elementi: per esempio, con 4.096 elementi non ordinati, ci sono 4.084 operazioni di scambio. Questi numeri cambiano casualmente da test a test.
- Tuttavia, con elementi ordinati in ordine decrescente, abbiamo solo la metà delle operazioni di swap rispetto agli elementi! Questo perché, quando scambiamo, non solo mettiamo l’elemento più piccolo al posto giusto, ma anche il rispettivo partner di scambio.
Con otto elementi, per esempio, abbiamo quattro operazioni di scambio. Nelle prime quattro iterazioni, ne abbiamo una ciascuno e nelle iterazioni da cinque a otto, nessuna (tuttavia l’algoritmo continua a funzionare fino alla fine):

Inoltre, possiamo leggere dalle misurazioni:
- La ragione per cui Selection Sort è così più lento con elementi ordinati in ordine decrescente può essere trovata nel numero di assegnazioni di variabili locali (
minPosemin) quando si cerca l’elemento più piccolo. Mentre con 8.192 elementi non ordinati, abbiamo 69.378 di queste assegnazioni, con elementi ordinati in ordine decrescente, ci sono 16.785.407 tali assegnazioni – cioè 242 volte tanto!
Perché questa enorme differenza?
Analisi del tempo di esecuzione della ricerca dell’elemento più piccolo
Per gli elementi ordinati in ordine decrescente, l’ordine di grandezza può essere derivato dalla figura appena sopra. La ricerca dell’elemento più piccolo è limitata al triangolo delle caselle arancione e arancione-blu. Nella parte superiore arancione, i numeri in ogni casella diventano più piccoli; nella parte destra arancione-blu, i numeri aumentano ancora.
Le operazioni di assegnazione hanno luogo in ogni casella arancione e nella prima delle caselle arancio-blu. Il numero di operazioni di assegnazione per minPos e min è quindi, in senso figurato, circa “un quarto del quadrato” – matematicamente e precisamente, è ¼ n² + n – 1.
Per gli elementi non ordinati, dovremmo penetrare molto più a fondo nella questione. Questo non solo andrebbe oltre lo scopo di questo articolo, ma dell’intero blog.
Quindi, limito la mia analisi a un piccolo programma demo che misura quante assegnazioni minPos/min ci sono quando si cerca l’elemento più piccolo in un array non ordinato. Ecco i valori medi dopo 100 iterazioni (un piccolo estratto; i risultati completi possono essere trovati qui):
| n | numero medio di assegnazioni minPos/min |
|---|---|
| 1.024 | 7.08 |
| 4.096 | 8.61 |
| 16.385 | 8.94 |
| 65.536 | 11.81 |
| 262.144 | 12.22 |
| 1.048.576 | 14.26 |
| 4.194.304 | 14.71 |
| 16.777.216 | 16.44 |
| 67.108.864 | 17.92 |
| 268.435.456 | 20.27 |
Ecco un diagramma con asse x logaritmico:

Il grafico mostra molto bene che abbiamo una crescita logaritmica, cioè, ad ogni raddoppio del numero di elementi, il numero di assegnazioni aumenta solo di un valore costante. Come ho detto, non mi addentrerò più a fondo negli sfondi matematici.
Questa è la ragione per cui queste assegnazioni minPos/min sono poco significative negli array non ordinati.
Altre caratteristiche di Selection Sort
Nelle sezioni seguenti, discuterò la complessità dello spazio, la stabilità e la parallelabilità di Selection Sort.
Complessità dello spazio di Selection Sort
La complessità dello spazio di Selection Sort è costante poiché non abbiamo bisogno di ulteriore spazio di memoria a parte le variabili di loop i e j e le variabili ausiliarie length, minPos e min.
Ovvero, non importa quanti elementi ordiniamo – dieci o dieci milioni – abbiamo sempre e solo bisogno di queste cinque variabili aggiuntive. Notiamo il tempo costante come O(1).
Stabilità di Selection Sort
Selection Sort sembra stabile a prima vista: Se la parte non ordinata contiene diversi elementi con la stessa chiave, il primo dovrebbe essere aggiunto per primo alla parte ordinata.
Ma le apparenze sono ingannevoli. Perché scambiando due elementi nel secondo sottofase dell’algoritmo, può succedere che alcuni elementi nella parte non ordinata non abbiano più l’ordine originale. Questo, a sua volta, porta al fatto che non appaiono più nell’ordine originale nella parte ordinata.
Un esempio può essere costruito molto semplicemente. Supponiamo di avere due elementi diversi con chiave 2 e uno con chiave 1, disposti come segue, e di ordinarli con Selection Sort:

Nel primo passo, il primo e l’ultimo elemento vengono scambiati. Così l’elemento “DUE” finisce dietro l’elemento “due” – l’ordine di entrambi gli elementi è scambiato.
Nel secondo passo, l’algoritmo confronta i due elementi posteriori. Entrambi hanno la stessa chiave, 2. Quindi nessun elemento viene scambiato.
Nel terzo passo, rimane solo un elemento; questo viene automaticamente considerato ordinato.
I due elementi con la chiave 2 sono quindi stati scambiati nel loro ordine iniziale – l’algoritmo è instabile.
Variante stabile di Selection Sort
Selection Sort può essere reso stabile non scambiando l’elemento più piccolo con il primo nel passo due, ma spostando tutti gli elementi tra il primo e l’elemento più piccolo di una posizione a destra e inserendo l’elemento più piccolo all’inizio.
Anche se la complessità temporale rimarrà la stessa a causa di questo cambiamento, gli spostamenti aggiuntivi porteranno ad una degradazione significativa delle prestazioni, almeno quando si ordina un array.
Con una lista collegata, tagliare e incollare l’elemento da ordinare potrebbe essere fatto senza alcuna perdita significativa di prestazioni.
Parallelizzabilità di Selection Sort
Non possiamo parallelizzare il ciclo esterno perché cambia il contenuto dell’array in ogni iterazione.
Il ciclo interno (ricerca dell’elemento più piccolo) può essere parallelizzato dividendo l’array, cercando l’elemento più piccolo in ogni sotto-array in parallelo, e unendo i risultati intermedi.
Selection Sort vs. Insertion Sort
Quale algoritmo è più veloce, Selection Sort o Insertion Sort?
Confrontiamo le misure delle mie implementazioni Java. Con Insertion Sort, la complessità temporale del caso migliore è O(n) e ha richiesto meno di un millisecondo per un massimo di 524.288 elementi. Quindi, nel caso migliore, Insertion Sort è, per qualsiasi numero di elementi, ordini di grandezza più veloce di Selection Sort.
| n | Selection Sort unsorted |
Insertion Sort unsorted |
Selection Sort descending |
Insertion Sort descending |
|---|---|---|---|---|
| … | … | … | … | … |
| 16.384 | 27,9 ms | 21,9 ms | 65,6 ms | 43,6 ms |
| 32.768 | 108,0 ms | 87,9 ms | 265,4 ms | 175,8 ms |
| 65.536 | 434,0 ms | 350,4 ms | 1.052,2 ms | 697,6 ms |
| 131.072 | 1.729,8 ms | 1.398,9 ms | 4.209,9 ms | 2.840,0 ms |
| 262.144 | 6.913,4 ms | 5.706,8 ms | 16.863,7 ms | 11.517,4 ms |
| 524.288 | 27.649,8 ms | 23.009,7 ms | 67.537,8 ms | 46.309,3 ms |
E ancora una volta come diagramma:

Insertion Sort è, quindi, non solo più veloce di Selection Sort nel caso migliore ma anche nel caso medio e peggiore.
La ragione di questo è che Insertion Sort richiede, in media, la metà dei confronti. Come promemoria, con Insertion Sort, abbiamo confronti e spostamenti in media fino alla metà degli elementi ordinati; con Selection Sort, dobbiamo cercare l’elemento più piccolo in tutti gli elementi non ordinati in ogni passo.
Selection Sort ha significativamente meno operazioni di scrittura, quindi Selection Sort può essere più veloce quando le operazioni di scrittura sono costose. Questo non è il caso delle scritture sequenziali sugli array, dato che queste sono per lo più effettuate nella cache della CPU.
In pratica, Selection Sort non è quindi quasi mai usato.
Sommario
Selection Sort è un algoritmo di ordinamento facile da implementare, e nella sua tipica implementazione instabile, con una complessità temporale media, nel caso migliore e nel caso peggiore di O(n²).
Selection Sort è più lento di Insertion Sort, ed è per questo che è raramente usato nella pratica.
Troverai altri algoritmi di ordinamento in questa panoramica di tutti gli algoritmi di ordinamento e le loro caratteristiche nella prima parte della serie di articoli.
Se ti è piaciuto l’articolo, sentiti libero di condividerlo usando uno dei pulsanti di condivisione alla fine. Vuoi essere informato via e-mail quando pubblico un nuovo articolo? Allora usa il seguente modulo per iscriverti alla mia newsletter.