Biografia
Johannes Kepler è oggi ricordato soprattutto per aver scoperto le tre leggi del moto planetario che portano il suo nome, pubblicate nel 1609 e nel 1619.) Fece anche un lavoro importante nell’ottica (1604, 1611), scoprì due nuovi poliedri regolari (1619), diede il primo trattamento matematico dell’impacchettamento ravvicinato di sfere uguali (portando a una spiegazione della forma delle celle di un nido d’ape, 1611), diede la prima prova del funzionamento dei logaritmi (1624), e ideò un metodo per trovare i volumi dei solidi di rivoluzione che (col senno di poi!) può essere visto come un contributo allo sviluppo del calcolo (1615, 1616). Inoltre, calcolò le tavole astronomiche più esatte finora conosciute, la cui continua accuratezza fece molto per stabilire la verità dell’astronomia eliocentrica (Tavole Rudolphine, Ulm, 1627).
Si conserva una grande quantità di corrispondenza di Keplero. Molte delle sue lettere sono quasi l’equivalente di un articolo scientifico (non esistevano ancora le riviste scientifiche), e i corrispondenti sembrano averle conservate perché erano interessanti. Di conseguenza, sappiamo molto della vita di Keplero e del suo carattere. È in parte a causa di questo che Keplero ha avuto una carriera come personaggio più o meno fittizio (vedi nota storiografica sotto).
Infanzia
Keplero nacque nella piccola città di Weil der Stadt in Svevia e si trasferì nella vicina Leonberg con i suoi genitori nel 1576. Suo padre era un soldato mercenario e sua madre la figlia di un oste. Johannes fu il loro primo figlio. Suo padre lasciò casa per l’ultima volta quando Johannes aveva cinque anni, e si crede che sia morto nella guerra nei Paesi Bassi. Da bambino, Kepler visse con sua madre nella locanda del nonno. Racconta che era solito aiutare servendo nella locanda. Si immagina che i clienti fossero a volte stupiti dall’insolita competenza del bambino in aritmetica.
La prima educazione di Keplero fu in una scuola locale e poi in un seminario vicino, dal quale, con l’intenzione di essere ordinato, andò ad iscriversi all’Università di Tubinga, allora (come oggi) un bastione dell’ortodossia luterana.
Le opinioni di Keplero
Per tutta la sua vita, Keplero fu un uomo profondamente religioso. Tutti i suoi scritti contengono numerosi riferimenti a Dio, ed egli vedeva il suo lavoro come un adempimento del suo dovere cristiano di comprendere le opere di Dio. Essendo l’uomo, come credeva Keplero, fatto a immagine di Dio, era chiaramente in grado di comprendere l’Universo che Egli aveva creato. Inoltre, Keplero era convinto che Dio avesse fatto l’Universo secondo un piano matematico (una credenza che si trova nelle opere di Platone e associata a Pitagora). Poiché all’epoca era generalmente accettato che la matematica fornisse un metodo sicuro per arrivare alle verità sul mondo (le nozioni e i postulati comuni di Euclide erano considerati effettivamente veri), abbiamo qui una strategia per comprendere l’universo. Dato che alcuni autori hanno dato a Keplero la nomea di irrazionale, vale la pena notare che questa epistemologia piuttosto speranzosa è davvero molto lontana dalla convinzione del mistico che le cose possono essere comprese solo in modo impreciso che si basa su intuizioni che non sono soggette alla ragione. Keplero in effetti ringrazia ripetutamente Dio per avergli concesso delle intuizioni, ma le intuizioni sono presentate come razionali.
Formazione universitaria
A quel tempo, era usuale per tutti gli studenti di un’università frequentare corsi di “matematica”. In principio questo includeva le quattro scienze matematiche: aritmetica, geometria, astronomia e musica. Sembra, tuttavia, che ciò che veniva insegnato dipendeva dalla particolare università. A Tubinga a Keplero fu insegnata l’astronomia da uno dei principali astronomi del tempo, Michael Mästlin (1550 – 1631). L’astronomia del curriculum era, naturalmente, l’astronomia geocentrica, cioè la versione corrente del sistema tolemaico, in cui tutti e sette i pianeti – Luna, Mercurio, Venere, Sole, Marte, Giove e Saturno – si muovevano intorno alla Terra, e le loro posizioni rispetto alle stelle fisse venivano calcolate combinando i movimenti circolari. Questo sistema era più o meno in accordo con le nozioni correnti (aristoteliche) della fisica, anche se c’erano alcune difficoltà, come il fatto che si potesse considerare “uniforme” (e quindi accettabile come ovviamente eterno) un moto circolare che non era uniforme attorno al proprio centro ma attorno ad un altro punto (chiamato “equante”). Tuttavia, sembra che nel complesso gli astronomi (che si consideravano “matematici”) fossero contenti di continuare a calcolare le posizioni dei pianeti e lasciare ai filosofi naturali il compito di preoccuparsi se i modelli matematici corrispondessero ai meccanismi fisici. Keplero non aveva questo atteggiamento. Il suo primo lavoro pubblicato (1596) propone di considerare i percorsi reali dei pianeti, non i cerchi usati per costruirli.
A Tubinga, Keplero studiò non solo matematica ma anche greco ed ebraico (entrambi necessari per leggere le scritture nelle loro lingue originali). L’insegnamento era in latino. Alla fine del suo primo anno Keplero ha preso ‘A’ in tutto tranne che in matematica. Probabilmente Mästlin stava cercando di dirgli che poteva fare meglio, perché Keplero era in effetti uno dei selezionati allievi ai quali scelse di insegnare l’astronomia più avanzata introducendoli al nuovo sistema cosmologico eliocentrico di Copernico. Fu da Mästlin che Keplero apprese che la prefazione a Sulle rivoluzioni, che spiegava che questa era “solo matematica”, non era di Copernico. Keplero sembra aver accettato quasi istantaneamente che il sistema copernicano fosse fisicamente vero; le sue ragioni per accettarlo saranno discusse in relazione al suo primo modello cosmologico (vedi sotto).
Sembra che anche nei giorni in cui Keplero era studente ci fossero indicazioni che le sue credenze religiose non fossero del tutto in accordo con il luteranesimo ortodosso corrente a Tubinga e formulato nella Confessio Augustana Ⓣ. I problemi di Keplero con questa ortodossia protestante riguardavano la supposta relazione tra materia e “spirito” (un’entità non materiale) nella dottrina dell’Eucaristia. Questo si collega all’astronomia di Keplero nella misura in cui egli apparentemente trovò delle difficoltà intellettuali simili nello spiegare come la ‘forza’ dal Sole potesse influenzare i pianeti. Nei suoi scritti, Keplero è solito esporre le sue opinioni sulla linea – il che è molto comodo per gli storici. Nella vita reale, sembra probabile che una simile tendenza all’apertura abbia portato le autorità di Tubinga a nutrire dubbi fondati sulla sua ortodossia religiosa. Questi possono spiegare perché Mästlin persuase Keplero ad abbandonare i piani per l’ordinazione e invece prendere un posto di insegnante di matematica a Graz. L’intolleranza religiosa si acuì negli anni seguenti. Keplero fu scomunicato nel 1612. Questo gli causò molto dolore, ma nonostante la sua (ormai) posizione sociale relativamente alta, come matematico imperiale, non riuscì mai a far rimuovere il divieto.
Il primo modello cosmologico di Keplero (1596)
Invece dei sette pianeti dell’astronomia geocentrica standard, il sistema copernicano ne aveva solo sei, essendo la Luna diventata un corpo di tipo precedentemente sconosciuto all’astronomia, che Keplero avrebbe poi chiamato “satellite” (un nome che coniò nel 1610 per descrivere le lune che Galileo aveva scoperto orbitare intorno a Giove, che letteralmente significa “attendente”). Perché sei pianeti?
Inoltre, nell’astronomia geocentrica non c’era modo di usare le osservazioni per trovare le dimensioni relative degli orbi planetari; si assumeva semplicemente che fossero in contatto. Questo sembrava non richiedere alcuna spiegazione, poiché si adattava bene alla convinzione dei filosofi naturali che l’intero sistema fosse girato dal movimento della sfera più esterna, una (o forse due) oltre la sfera delle stelle “fisse” (quelle il cui schema forma le costellazioni), oltre la sfera di Saturno. Nel sistema copernicano, il fatto che la componente annuale di ogni moto planetario fosse un riflesso del moto annuale della Terra permetteva di usare le osservazioni per calcolare la dimensione del percorso di ogni pianeta, e si scopriva che c’erano spazi enormi tra i pianeti. Perché questi spazi particolari?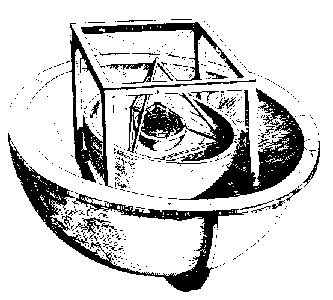
La risposta di Keplero a queste domande, descritta nel suo Mysterium cosmographicum Ⓣ, Tubinga, 1596, appare bizzarra ai lettori del ventesimo secolo (vedi la figura a destra). Suggerì che se una sfera fosse disegnata per toccare l’interno del percorso di Saturno, e un cubo fosse inscritto nella sfera, allora la sfera inscritta in quel cubo sarebbe la sfera che circoscrive il percorso di Giove. Se poi un tetraedro regolare fosse disegnato nella sfera che inscrive il percorso di Giove, l’insfera del tetraedro sarebbe la sfera che circoscrive il percorso di Marte, e così verso l’interno, mettendo il dodecaedro regolare tra Marte e la Terra, l’icosaedro regolare tra la Terra e Venere, e l’ottaedro regolare tra Venere e Mercurio. Questo spiega perfettamente il numero di pianeti: ci sono solo cinque solidi regolari convessi (come è dimostrato negli Elementi di Euclide, Libro 13). Dà anche un adattamento convincente con le dimensioni dei percorsi come dedotti da Copernico, l’errore maggiore essendo meno del 10% (che è spettacolarmente buono per un modello cosmologico anche ora). Keplero non si è espresso in termini di errori percentuali, e il suo è di fatto il primo modello cosmologico matematico, ma è facile capire perché credeva che le prove osservative supportassero la sua teoria.
Keplero vedeva la sua teoria cosmologica come una prova della teoria copernicana. Prima di presentare la propria teoria, ha fornito argomenti per stabilire la plausibilità della teoria copernicana stessa. Keplero afferma che i suoi vantaggi rispetto alla teoria geocentrica stanno nel suo maggiore potere esplicativo. Per esempio, la teoria copernicana può spiegare perché Venere e Mercurio non si vedono mai molto lontano dal Sole (si trovano tra la Terra e il Sole) mentre nella teoria geocentrica non c’è spiegazione di questo fatto. Keplero elenca nove di queste domande nel primo capitolo del Mysterium cosmographicum Ⓣ.
Keplero realizzò questo lavoro mentre insegnava a Graz, ma il libro fu visto in stampa a Tubinga da Mästlin. L’accordo con i valori dedotti dall’osservazione non era esatto, e Keplero sperava che migliori osservazioni avrebbero migliorato l’accordo, così inviò una copia del Mysterium cosmographicum a uno dei più importanti astronomi osservatori dell’epoca, Tycho Brahe (1546 – 1601). Tycho, che allora lavorava a Praga (all’epoca capitale del Sacro Romano Impero), aveva infatti già scritto a Mästlin in cerca di un assistente matematico. Keplero ottenne il lavoro.
La ‘guerra con Marte’
Naturalmente, le priorità di Tycho non erano le stesse di Keplero, e Keplero si trovò presto a lavorare sull’intrattabile problema dell’orbita di Marte. Continuò a lavorare su questo dopo che Tycho morì (nel 1601) e Keplero gli succedette come matematico imperiale. Convenzionalmente, le orbite erano composte da cerchi, e piuttosto pochi valori osservativi erano necessari per fissare i raggi relativi e le posizioni dei cerchi. Tycho aveva fatto un numero enorme di osservazioni e Keplero decise di farne il miglior uso possibile. Essenzialmente, aveva a disposizione così tante osservazioni che una volta che aveva costruito una possibile orbita era in grado di controllarla con ulteriori osservazioni fino a raggiungere un accordo soddisfacente. Keplero concluse che l’orbita di Marte era un’ellisse con il Sole in uno dei suoi fuochi (un risultato che, esteso a tutti i pianeti, è ora chiamato “Prima legge di Keplero”), e che una linea che unisce il pianeta al Sole spazza via aree uguali in tempi uguali man mano che il pianeta descrive la sua orbita (“Seconda legge di Keplero”), cioè l’area viene usata come misura del tempo. Dopo che questo lavoro fu pubblicato su Astronomia nova, … Ⓣ, Heidelberg, 1609, Keplero trovò orbite per gli altri pianeti, stabilendo così che le due leggi valevano anche per loro. Entrambe le leggi mettono in relazione il moto del pianeta con il Sole; il copernicanesimo di Keplero fu cruciale per il suo ragionamento e per le sue deduzioni.
Il processo effettivo di calcolo per Marte fu immensamente laborioso – ci sono quasi mille fogli di aritmetica superstiti – e Keplero stesso si riferisce a questo lavoro come “la mia guerra con Marte”, ma il risultato fu un’orbita che concorda con i risultati moderni così esattamente che il confronto deve tenere conto dei cambiamenti secolari dell’orbita dai tempi di Keplero.
Errore osservazionale
Per il metodo di Keplero di verificare le possibili orbite rispetto alle osservazioni, era cruciale avere un’idea di ciò che doveva essere accettato come accordo adeguato. Da qui nasce il primo uso esplicito del concetto di errore osservazionale. Keplero potrebbe aver dovuto questa nozione almeno in parte a Tycho, che faceva controlli dettagliati sulle prestazioni dei suoi strumenti (vedi la biografia di Brahe).
Ottica, e la nuova stella del 1604
Il lavoro su Marte fu sostanzialmente completato entro il 1605, ma ci furono ritardi nella pubblicazione del libro. Nel frattempo, in risposta alle preoccupazioni sul diverso diametro apparente della Luna quando viene osservata direttamente e quando viene osservata con una camera oscura, Keplero fece alcuni lavori sull’ottica, e arrivò alla prima teoria matematica corretta della camera oscura e alla prima spiegazione corretta del funzionamento dell’occhio umano, con un’immagine capovolta che si forma sulla retina. Questi risultati furono pubblicati in Ad Vitellionem paralipomena, quibus astronomiae pars optica traditur Ⓣ, Francoforte, 1604. Scrisse anche sulla Stella Nuova del 1604, ora solitamente chiamata ‘supernova di Keplero’, rifiutando numerose spiegazioni, e osservando ad un certo punto che naturalmente questa stella potrebbe essere solo una creazione speciale ‘ma prima di arrivare a penso che dovremmo provare tutto il resto’ De stella nova Ⓣ, Praga, 1606, Capitolo 22, KGW 1, p. 257, riga 23.
Dopo l’uso del telescopio da parte di Galileo per scoprire le lune di Giove, pubblicato nel suo Messaggero siderale (Venezia, 1610), al quale Keplero aveva scritto una risposta entusiasta (1610), Keplero scrisse uno studio sulle proprietà delle lenti (il primo lavoro di questo tipo sull’ottica) in cui presentò un nuovo disegno di telescopio, utilizzando due lenti convesse (Dioptrice, Praga, 1611). Questo progetto, in cui l’immagine finale è invertita, ebbe un tale successo che ora è solitamente conosciuto non come telescopio kepleriano ma semplicemente come telescopio astronomico.
Lasciare Praga per Linz
Gli anni di Keplero a Praga furono relativamente tranquilli e scientificamente estremamente produttivi. Infatti, anche quando le cose andavano male, sembra che non abbia mai permesso alle circostanze esterne di impedirgli di continuare il suo lavoro. Le cose cominciarono ad andare molto male alla fine del 1611. Per prima cosa, suo figlio di sette anni morì. Keplero scrisse ad un amico che questa morte era particolarmente difficile da sopportare perché il bambino gli ricordava molto se stesso a quell’età. Poi morì la moglie di Keplero. Poi l’imperatore Rodolfo, la cui salute stava cedendo, fu costretto ad abdicare in favore di suo fratello Mattia, che, come Rodolfo, era cattolico ma (a differenza di Rodolfo) non credeva nella tolleranza dei protestanti. Keplero dovette lasciare Praga. Prima di partire fece trasferire il corpo della moglie nella tomba del figlio e scrisse un epitaffio in latino per loro. Lui e i figli rimasti si trasferirono a Linz (ora in Austria).
Matrimonio e botti di vino
Keplero sembra aver sposato la sua prima moglie, Barbara, per amore (anche se il matrimonio fu organizzato tramite un mediatore). Il secondo matrimonio, nel 1613, fu una questione di necessità pratica: aveva bisogno di qualcuno che si occupasse dei bambini. La nuova moglie di Keplero, Susanna, ebbe un corso intensivo sul carattere di Keplero: la lettera dedicatoria al libro risultante spiega che durante i festeggiamenti del matrimonio notò che i volumi delle botti di vino erano stimati per mezzo di un’asta infilata diagonalmente attraverso il buco del culo, e cominciò a chiedersi come potesse funzionare. Il risultato fu uno studio dei volumi dei solidi di rivoluzione Nova stereometria doliorum … Ⓣ, Linz, 1615, in cui Keplero, basandosi sul lavoro di Archimede, utilizzò una risoluzione in ‘indivisibili’. Questo metodo fu poi sviluppato da Bonaventura Cavalieri (c. 1598 – 1647) e fa parte dell’antenato del calcolo infinitesimale.
L’Armonia del Mondo
Il compito principale di Keplero come matematico imperiale era quello di scrivere tavole astronomiche, basate sulle osservazioni di Tycho, ma quello che voleva veramente fare era scrivere L’Armonia del Mondo, pianificato dal 1599 come sviluppo del suo Mistero del Cosmo. Questa seconda opera sulla cosmologia (Harmonices mundi libri V Ⓣ, Linz, 1619) presenta un modello matematico più elaborato del precedente, anche se i poliedri ci sono ancora. La matematica in quest’opera include il primo trattamento sistematico delle tassellazioni, una prova che ci sono solo tredici poliedri uniformi convessi (i solidi archimedei) e il primo resoconto di due poliedri regolari non convessi (tutti nel Libro 2). L’Armonia del Mondo contiene anche quella che ora è conosciuta come ‘Terza Legge di Keplero’, che per qualsiasi due pianeti il rapporto dei quadrati dei loro periodi sarà lo stesso del rapporto dei cubi dei raggi medi delle loro orbite. Dalla prima, Keplero aveva cercato una regola che mettesse in relazione le dimensioni delle orbite con i periodi, ma non c’era stata una lenta serie di passi verso questa legge come era successo per le altre due. Infatti, anche se la terza legge gioca un ruolo importante in alcune delle sezioni finali della versione stampata dell’Armonia del mondo, non è stata effettivamente scoperta fino a quando il lavoro era in stampa. Keplero fece delle revisioni dell’ultimo minuto. Lui stesso racconta la storia del successo finale:
…e se volete il momento esatto, fu concepita mentalmente l’8 marzo di quest’anno milleseicentodiciotto, ma sottoposta a calcolo in modo sfortunato, e quindi respinta come falsa, e infine ritornando il 15 maggio e adottando una nuova linea di attacco, prese d’assalto le tenebre della mia mente. Era così forte l’appoggio della combinazione del mio lavoro di diciassette anni sulle osservazioni di Brahe e del presente studio, che cospiravano insieme, che all’inizio credevo di sognare, e di assumere la mia conclusione tra le mie premesse fondamentali. Ma è assolutamente certo ed esatto che “la proporzione tra i tempi periodici di due pianeti qualsiasi è precisamente la proporzione sesquialterata delle loro distanze medie …”
(Harmonice mundi Book 5, Chapter 3, trans. Aiton, Duncan and Field, p. 411).
Processo per stregoneria
Mentre Keplero stava lavorando alla sua Armonia del Mondo, sua madre fu accusata di stregoneria. Arruolò l’aiuto della facoltà di legge di Tubinga. Katharina Kepler fu alla fine rilasciata, almeno in parte come risultato di obiezioni tecniche derivanti dall’incapacità delle autorità di seguire le corrette procedure legali nell’uso della tortura. I documenti sopravvissuti sono agghiaccianti. Tuttavia, Kepler ha continuato a lavorare. Nella carrozza, durante il suo viaggio nel Württemberg per difendere la madre, lesse un’opera sulla teoria musicale di Vincenzo Galilei (1520 circa – 1591, padre di Galileo), alla quale ci sono numerosi riferimenti ne L’armonia del mondo.
Tabelle astronomiche
Il calcolo delle tabelle, la normale attività per un astronomo, comportava sempre una pesante aritmetica. Keplero fu quindi felice quando nel 1616 si imbatté nel lavoro di Napier sui logaritmi (pubblicato nel 1614). Tuttavia, Mästlin gli disse subito che era indecoroso per un matematico serio gioire per un semplice aiuto al calcolo e in secondo luogo che non era saggio fidarsi dei logaritmi perché nessuno capiva come funzionavano. (La risposta di Keplero alla seconda obiezione fu di pubblicare una prova del funzionamento dei logaritmi, basata su una fonte impeccabilmente rispettabile: Il libro 5 degli Elementi di Euclide. Keplero calcolò delle tavole di logaritmi a otto cifre, che furono pubblicate con le Tavole Rudolphine (Ulm, 1628). Le tavole astronomiche utilizzavano non solo le osservazioni di Tycho, ma anche le prime due leggi di Keplero. Tutte le tavole astronomiche che facevano uso di nuove osservazioni erano accurate per i primi anni dopo la pubblicazione. Ciò che era notevole delle Tavole di Rodolfo era che si dimostrarono accurate per decenni. E man mano che gli anni aumentavano, la continua accuratezza delle tavole era, naturalmente, vista come un argomento per la correttezza delle leggi di Keplero, e quindi per la correttezza dell’astronomia eliocentrica. L’adempimento da parte di Keplero del suo noioso compito ufficiale di matematico imperiale portò alla realizzazione del suo desiderio più caro, quello di aiutare a stabilire il copernicanesimo.
Wallenstein
Quando furono pubblicate le Tavole Rodolfo, Keplero non lavorava più per l’imperatore (aveva lasciato Linz nel 1626), ma per Albrecht von Wallenstein (1583 – 1632), uno dei pochi capi militari di successo nella guerra dei trent’anni (1618 – 1648). Keplero naturalmente doveva obbedire, ma sottolinea ripetutamente che non crede che si possano fare previsioni precise. Come la maggior parte delle persone dell’epoca, Keplero accettava il principio dell’astrologia, che i corpi celesti potessero influenzare ciò che accadeva sulla Terra (gli esempi più chiari sono il Sole che causa le stagioni e la Luna le maree), ma come copernicano non credeva nella realtà fisica delle costellazioni. La sua astrologia era basata solo sugli angoli tra le posizioni dei corpi celesti (“aspetti astrologici”). Egli esprime un totale disprezzo per i complicati sistemi dell’astrologia convenzionale.
Morte
Keplero morì a Regensburg, dopo una breve malattia. Si trovava in città mentre andava a riscuotere del denaro che gli doveva in relazione alle Tavole Rudolphine. Fu sepolto nella chiesa locale, ma questa fu distrutta nel corso della Guerra dei Trent’anni e della tomba non è rimasto nulla.
Nota storiografica
Molto è stato fatto a volte su presunti elementi non razionali nell’attività scientifica di Keplero. Gli astrologi credenti spesso affermano che il suo lavoro fornisce un antecedente scientificamente rispettabile al loro. Nel suo influente Sleepwalkers il defunto Arthur Koestler ha trasformato la battaglia di Keplero con Marte in un argomento per l’intrinseca irrazionalità della scienza moderna. Ci sono stati molti taciti seguaci di queste due persuasioni. Entrambe sono, tuttavia, basate su una lettura molto parziale del lavoro di Keplero. In particolare, Koestler sembra non aver avuto la competenza matematica per capire le procedure di Keplero. Uno studio più approfondito mostra che Koestler era semplicemente in errore nella sua valutazione.
L’elemento non-razionale veramente importante nel lavoro di Keplero è il suo cristianesimo. L’uso esteso e riuscito della matematica da parte di Keplero fa sembrare il suo lavoro “moderno”, ma in realtà abbiamo a che fare con un filosofo naturale cristiano, per il quale la comprensione della natura dell’universo includeva la comprensione della natura del suo Creatore.