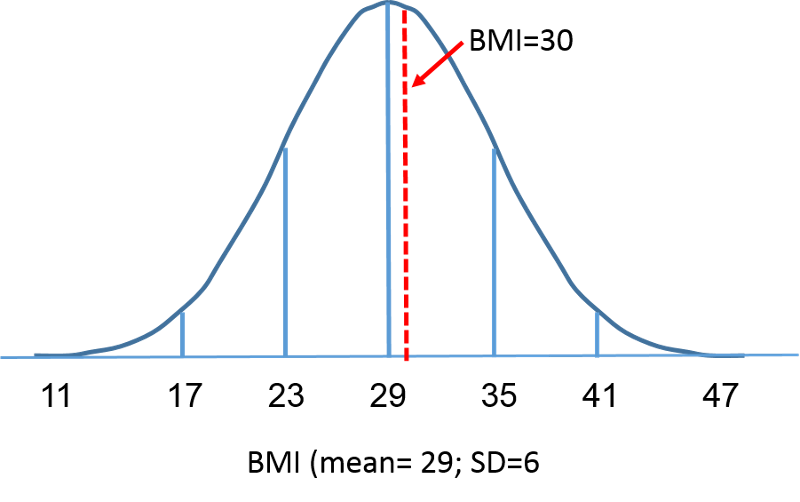
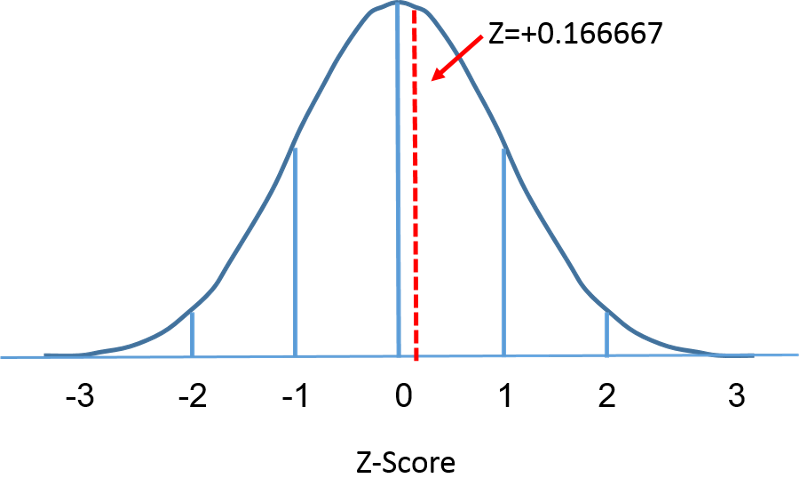
La distribuzione normale standard è una distribuzione normale con una media di zero e una deviazione standard di 1. La distribuzione normale standard è centrata a zero e il grado in cui una data misura si discosta dalla media è dato dalla deviazione standard. Per la distribuzione normale standard, il 68% delle osservazioni si trova entro 1 deviazione standard dalla media; il 95% si trova entro due deviazioni standard dalla media; e il 99,9% si trova entro 3 deviazioni standard dalla media. Fino a questo punto, abbiamo usato “X” per indicare la variabile di interesse (ad esempio, X=BMI, X=altezza, X=peso). Tuttavia, quando usiamo una distribuzione normale standard, useremo “Z” per riferirci a una variabile nel contesto di una distribuzione normale standard. Dopo la standardizzazione, il BMI=30 discusso nella pagina precedente è mostrato qui sotto che giace 0,16667 unità sopra la media di 0 sulla distribuzione normale standard sulla destra.
 ====
====
Siccome l’area sotto la curva standard = 1, possiamo iniziare a definire più precisamente le probabilità di osservazione specifica. Per ogni dato Z-score possiamo calcolare l’area sotto la curva a sinistra di quello Z-score. La tabella nel riquadro sottostante mostra le probabilità per la distribuzione normale standard. Esaminate la tabella e notate che un punteggio “Z” di 0,0 indica una probabilità di 0,50 o 50%, e un punteggio “Z” di 1, cioè una deviazione standard sopra la media, indica una probabilità di 0,8413 o 84%. Questo perché una deviazione standard sopra e sotto la media comprende circa il 68% dell’area, quindi una deviazione standard sopra la media rappresenta la metà del 34%. Quindi, il 50% sotto la media più il 34% sopra la media ci dà l’84%.
Probabilità della distribuzione normale standard Z
![]()
Questa tabella è organizzata per fornire l’area sotto la curva a sinistra o meno di un valore specificato o “valore Z”. In questo caso, poiché la media è zero e la deviazione standard è 1, il valore Z è il numero di unità di deviazione standard lontano dalla media, e l’area è la probabilità di osservare un valore inferiore a quel particolare valore Z. Notate anche che la tabella mostra le probabilità a due cifre decimali di Z. Il posto delle unità e la prima cifra decimale sono mostrati nella colonna di sinistra, e la seconda cifra decimale è mostrata attraverso la riga superiore.
Ma torniamo alla domanda sulla probabilità che il BMI sia inferiore a 30, cioè, P(X<30). Possiamo rispondere a questa domanda usando la distribuzione normale standard. Le figure qui sotto mostrano le distribuzioni dell’IMC per gli uomini di 60 anni e la distribuzione normale standard fianco a fianco.
Distribuzione dell’IMC e distribuzione normale standard
 ====
====
L’area sotto ogni curva è una ma la scala dell’asse X è diversa. Si noti, tuttavia, che le aree a sinistra della linea tratteggiata sono le stesse. La distribuzione del BMI va da 11 a 47, mentre la distribuzione normale standardizzata, Z, va da -3 a 3. Vogliamo calcolare P(X < 30). Per fare questo possiamo determinare il valore Z che corrisponde a X = 30 e poi usare la tabella della distribuzione normale standardizzata sopra per trovare la probabilità o l’area sotto la curva. La seguente formula converte un valore X in un punteggio Z, chiamato anche punteggio standardizzato:

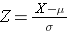
dove μ è la media e σ è la deviazione standard della variabile X.
Per calcolare P(X < 30) convertiamo X=30 nel suo corrispondente punteggio Z (questo si chiama standardizzare):

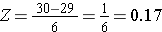
Quindi, P(X < 30) = P(Z < 0,17). Possiamo quindi cercare la probabilità corrispondente per questo punteggio Z dalla tabella di distribuzione normale standard, che mostra che P(X < 30) = P(Z < 0,17) = 0,5675. Quindi, la probabilità che un uomo di 60 anni abbia un BMI inferiore a 30 è del 56,75%.
Un altro esempio
Utilizzando la stessa distribuzione per il BMI, qual è la probabilità che un uomo di 60 anni abbia un BMI superiore a 35? In altre parole, qual è P(X > 35)? Di nuovo standardizziamo:

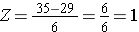
Ora andiamo alla tabella della distribuzione normale standard per cercare P(Z>1) e per Z=1.00 troviamo che P(Z<1.00) = 0.8413. Si noti, tuttavia, che la tabella dà sempre la probabilità che Z sia inferiore al valore specificato, cioè ci dà P(Z<1)=0,8413.
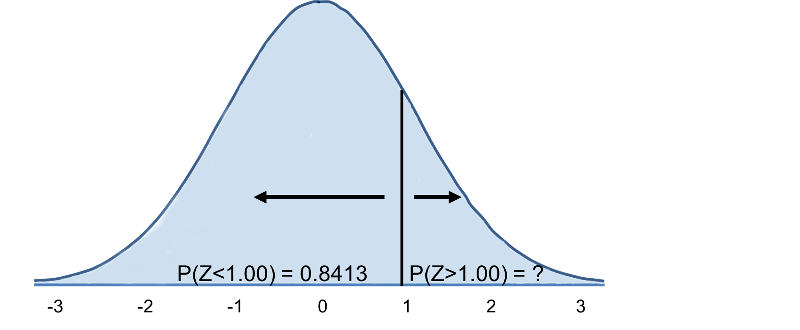
Quindi, P(Z>1)=1-0,8413=0,1587. Interpretazione: Quasi il 16% degli uomini di 60 anni ha un BMI superiore a 35.
Calcolatore di probabilità normali
![]()
![]()
Punteggi Z con R
In alternativa alla ricerca delle probabilità normali nella tabella o all’uso di Excel, possiamo usare R per calcolare le probabilità. Per esempio,
> pnorm(0)
Un punteggio Z di 0 (la media di qualsiasi distribuzione) ha il 50% dell’area a sinistra. Qual è la probabilità che un uomo di 60 anni nella popolazione di cui sopra abbia un BMI inferiore a 29 (la media)? Lo Z-score sarebbe 0, e pnorm(0)=0,5 o 50%.
Qual è la probabilità che un uomo di 60 anni abbia un BMI inferiore a 30? Lo Z-score era 0,16667.
> pnorm(0,16667)
Quindi, la probabilità è 56,6%.
Qual è la probabilità che un uomo di 60 anni avrà un BMI maggiore di 35?
35-29=6, che è una deviazione standard sopra la media. Quindi possiamo calcolare l’area a sinistra
> pnorm(1)
e poi sottrarre il risultato da 1.0.
1-0.8413447= 0.1586553
Quindi la probabilità che un uomo di 60 anni abbia un IMC superiore a 35 è del 15,8%.
Oppure, possiamo usare R per calcolare il tutto in un solo passo come segue:
> 1-pnorm(1)
Probabilità per un intervallo di valori

Qual è la probabilità che un uomo di 60 anni abbia un BMI tra 30 e 35? Si noti che questo è lo stesso che chiedere quale proporzione di uomini di 60 anni ha un BMI tra 30 e 35. In particolare, vogliamo P(30 < X < 35)? Abbiamo precedentemente calcolato P(30<X) e P(X<35); come si possono usare questi due risultati per calcolare la probabilità che l’IMC sia tra 30 e 35? Prova a formulare e rispondere da solo prima di guardare la spiegazione qui sotto.
Risposta