Selection Sort – Algoritmus, forráskód, időbonyolultság

Ez a cikk a Soroló algoritmusok sorozat része: Végső útmutató” című sorozatban és…

• leírja a Selection Sort működését,
• megtaláljuk a Selection Sort Java forráskódját,
• megmutatja, hogyan lehet levezetni az időbonyolultságát (bonyolult matematika nélkül)
• és ellenőrzi, hogy a Java implementáció teljesítménye megfelel-e az elvárt futásidejű viselkedésnek.

A teljes cikksorozat forráskódja megtalálható a GitHub tárolómban.

Példa: Playing Cards Sorting

A játékkártyák kézbe rendezése az Insertion Sort klasszikus példája.

A Selection Sort is szemléltethető játékkártyákkal. Nem ismerek senkit, aki így válogatja a kártyáit, de példaként elég jól működik 😉

Először is, az összes kártyát képpel felfelé az asztalra rakjuk magunk elé. Megkeresed a legkisebb lapot, és a kezed bal oldalára veszed. Aztán megkeresed a következő nagyobb lapot, és a legkisebbtől jobbra teszed, és így tovább, míg végül a legnagyobb lapot veszed fel a jobb szélsőjobbra.

Különbség a beillesztéses rendezéshez

A beillesztéses rendezésnél a következő, rendezetlen lapot vettük, és a rendezett lapok között a megfelelő helyre illesztettük.

A kiválasztásos rendezés valahogy fordítva működik: Kiválasztjuk a rendezetlen lapok közül a legkisebb lapot, majd – egymás után – beillesztjük a már rendezett lapok közé.

Selection Sort algoritmus

Az algoritmus legegyszerűbben egy példával magyarázható. A következő lépésekben bemutatom, hogyan rendezzük a tömböt Selection Sort algoritmussal:

1. lépés

A tömböt egy bal oldali, rendezett és egy jobb oldali, rendezetlen részre osztjuk. A rendezett rész kezdetben üres:

2. lépés

A jobb oldali, rendezetlen részben megkeressük a legkisebb elemet. Ehhez először megjegyezzük az első elemet, ami a 6. Átmegyünk a következő mezőbe, ahol találunk egy még kisebb elemet a 2. Végigmegyünk a tömb többi részén, még kisebb elemet keresve. Mivel ilyet nem találunk, maradunk a 2-nél, amit az első helyen lévő elemmel való felcseréléssel a megfelelő helyre teszünk. Ezután a tömbrészek határát egy mezővel jobbra toljuk:

3. lépés

Újra a jobb oldali, rendezetlen részben keressük a legkisebb elemet. Ezúttal ez a 3-as; kicseréljük a második helyen lévő elemmel:

4. lépés

Újra megkeressük a legkisebb elemet a jobb oldali részben. Ez a 4-es, ami már a megfelelő helyen van. Ebben a lépésben tehát nincs szükség cserélgetési műveletre, és csak a szakaszhatárt mozgatjuk:

5. lépés

A legkisebb elemként a 6-ost találjuk. Ezt felcseréljük a jobb oldali rész elején lévő elemmel, a 9-essel:

6. lépés

A fennmaradó két elem közül a 7-es a legkisebb. Ezt kicseréljük a 9-essel:

Algoritmus befejezve

Az utolsó elem automatikusan a legnagyobb, tehát a megfelelő helyen van. Az algoritmus befejeződött, és az elemek rendezve vannak:

Selection Sort Java forráskód

Ez a rész a Selection Sort egyszerű Java implementációját tartalmazza.

A külső ciklus végig iterálja a rendezni kívánt elemeket, és az utolsó előtti elem után ér véget. Ha ez az elem rendezve van, akkor az utolsó elem is automatikusan rendezésre kerül. A i ciklusváltozó mindig a jobb oldali, rendezetlen rész első elemére mutat.

Minden ciklusban a jobb oldali rész első elemét kezdetben a legkisebb elemnek min feltételezzük; pozícióját a minPos-ben tároljuk.

A belső ciklus ezután a jobb oldali rész második elemétől annak végéig iterál, és újra hozzárendeli a min és minPos pozíciókat, amikor még kisebb elemet talál.

A belső ciklus befejezése után a i (a jobb oldali rész eleje) és minPos pozíciók elemeit felcseréljük (hacsak nem ugyanaz az elem).

public class SelectionSort { public static void sort(int elements) { int length = elements.length; for (int i = 0; i < length - 1; i++) { // Search the smallest element in the remaining array int minPos = i; int min = elements; for (int j = i + 1; j < length; j++) { if (elements < min) { minPos = j; min = elements; } } // Swap min with element at pos i if (minPos != i) { elements = elements; elements = min; } } }}

A bemutatott kód abban különbözik a GitHub adattárban található SelectionSort osztálytól, hogy a SortAlgorithm interfészt valósítja meg, hogy könnyen felcserélhető legyen a tesztelési keretrendszerben.

Selection Sort Time Complexity

Nel jelöljük az elemek számát, példánkban n = 6.

A két egymásba ágyazott ciklus jelzi, hogy O(n²) időbonyolultsággal* van dolgunk. Ez akkor lesz így, ha mindkét ciklus olyan értékig iterál, amely lineárisan nő n-nel.

A külső ciklus esetében nyilvánvalóan ez a helyzet: n-1-ig számol.

Mi a helyzet a belső hurokkal?

Nézzük a következő ábrát:

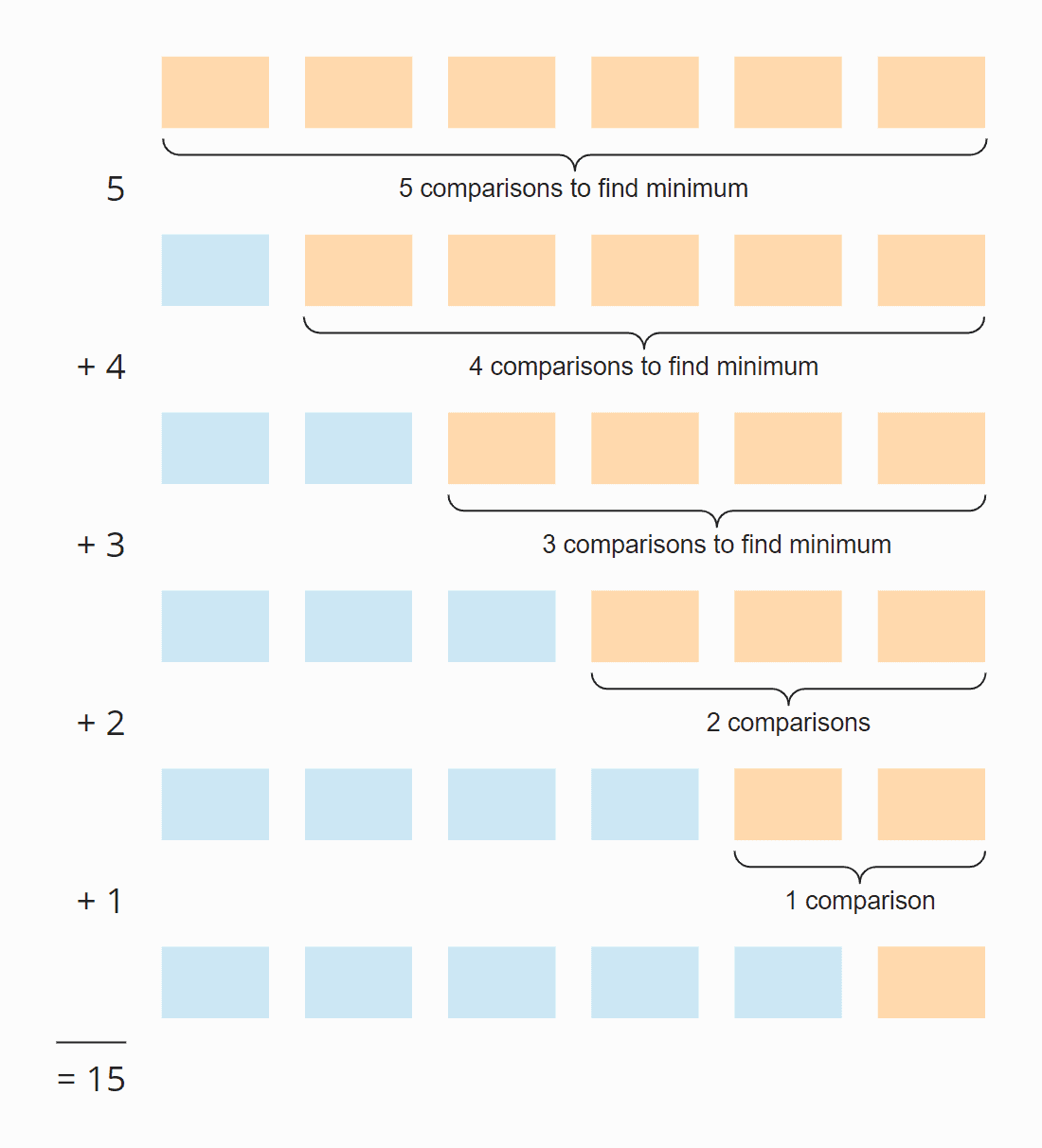
Minden lépésben az összehasonlítások száma eggyel kevesebb, mint a rendezetlen elemek száma. Összesen 15 összehasonlítás történik – függetlenül attól, hogy a tömb eredetileg rendezett-e vagy sem.

Ez a következőképpen is kiszámítható:

Hat elem szorozva öt lépéssel; osztva kettővel, mivel az összes lépés átlagában az elemek fele még rendezetlen:

6 × 5 × ½ = 30 × ½ = 15

Ha 6-ot n-nel helyettesítjük, akkor

n × (n – 1) × ½

Ha megszorozzuk, akkor ez:

½ n² – ½ n

Az n legnagyobb hatványa ebben a kifejezésben n². A legkisebb elem keresésének időbonyolultsága tehát O(n²) – más néven “kvadratikus idő”.

Nézzük most az elemek felcserélését. Minden lépésben (az utolsó kivételével) vagy egy elemet cserélünk, vagy egyet sem, attól függően, hogy a legkisebb elem már a megfelelő helyen van-e vagy sem. Így összességében maximum n-1 cserélgetési műveletünk van, azaz az időbonyolultság O(n) – más néven “lineáris idő”.

A teljes bonyolultság szempontjából csak a legnagyobb bonyolultsági osztály számít, ezért:

A Selection Sort átlagos, legjobb és legrosszabb esetre vonatkozó időbonyolultsága: O(n²)

* Az “időbonyolultság” és az “O-notáció” kifejezéseket ebben a cikkben példák és ábrák segítségével magyarázzuk.

A Java Selection Sort példa futási ideje

Elég az elméletből! Írtam egy tesztprogramot, amely a Selection Sort (és az ebben a sorozatban tárgyalt összes többi rendezési algoritmus) futási idejét a következőképpen méri:

• A rendezni kívánt elemek száma minden egyes iteráció után megduplázódik a kezdeti 1024 elemről 536 870 912 (= 229) elemre. Ekkora méretű tömböt nem lehet létrehozni Javában.
• Ha egy teszt 20 másodpercnél tovább tart, a tömböt nem bővítjük tovább.
• Minden tesztet rendezetlen, valamint emelkedő és csökkenő előre rendezett elemekkel futtatunk.
• A HotSpot fordítónak megengedjük, hogy két bemelegítő körrel optimalizálja a kódot. Ezt követően a teszteket a folyamat megszakításáig ismételjük.

Minden egyes iteráció után a program kiírja az összes korábbi mérési eredmény mediánját.

Íme a Selection Sort 50 iteráció után kapott eredménye (az áttekinthetőség kedvéért ez csak egy kivonat, a teljes eredmény itt található):

n	válogatás nélkül	felfelé	lefelé	lefelé
…	…	…	…
16.384	27,9 ms	26,8 ms	65,6 ms
32.768	108,0 ms	105,4 ms	265,4 ms
65.536	434,0 ms	424,3 ms	1.052,2 ms
131.072	1.729,8 ms	1.714,1 ms	4.209,9 ms
262.144	6.913,4 ms	6.880,2 ms	16.863,7 ms
524.288	27.649,8 ms	27.568,7 ms	67.537,8 ms

Itt a mérések még egyszer diagramként (ahol a szinte azonos értékek miatt a “rendezetlen” és a “felmenő” értékeket egy görbeként ábrázoltam):

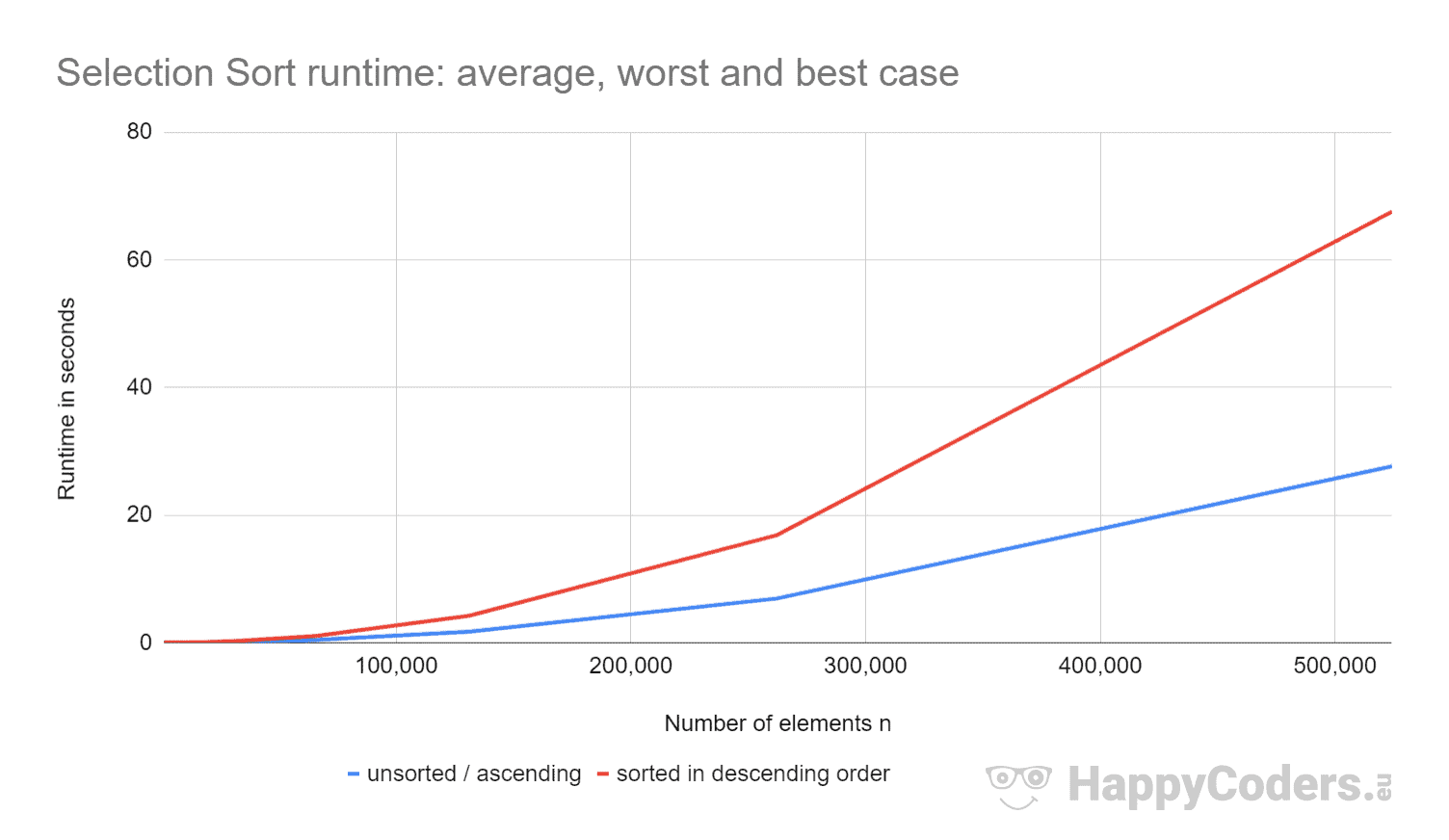
Jól látható, hogy

• ha az elemek számát megduplázzuk, a futási idő körülbelül megnégyszereződik – függetlenül attól, hogy az elemek előzetesen rendezettek-e vagy sem. Ez megfelel az O(n²) várható időbonyolultságnak.
• A futási idő emelkedő rendezett elemek esetén valamivel jobb, mint rendezetlen elemek esetén. Ennek az az oka, hogy a csereműveletekre, amelyeknek – mint fentebb elemeztük – nincs nagy jelentősége, itt nincs szükség.
• hogy a futási idő csökkenő rendezett elemek esetén lényegesen rosszabb, mint a rendezetlen elemek esetén.

Miért van ez?

A legrosszabb eset futási idejének elemzése

Egyáltalán, a legkisebb elem keresésének mindig ugyanannyi időt kellene igénybe vennie, függetlenül a kiindulási helyzettől. A csereműveleteknek pedig csak a csökkenő sorrendbe rendezett elemek esetében kellene valamivel többnek lennie (a csökkenő sorrendbe rendezett elemek esetében minden elemet cserélni kellene; a rendezetlen elemek esetében szinte minden elemet cserélni kellene).

A GitHub tárolómban található CountOperations programot használva láthatjuk a különböző műveletek számát. Itt vannak az eredmények a rendezetlen elemek és a csökkenő sorrendbe rendezett elemek esetében, egy táblázatban összefoglalva:

.

n	Összehasonlítások	Swaps rendezetlen	Swaps csökkenő	minPos/min válogatás nélkül	minPos/min csökkenő
…	…	…	…	…	…
512	130.816	504	256	2.866	66.047
1.024	523.776	1.017	512	6.439	263.167
2.048	2.096.128	2.042	1.024	14.727	1.050.623
4.096	8.386.560	4.084	2.048	30.758	4.198.399
8.192	33.550.336	8.181	4.096	69.378	16.785.407

A mért értékekből látható:

• A csökkenő sorrendbe rendezett elemekkel – a várakozásoknak megfelelően – ugyanannyi összehasonlítási műveletünk van, mint a rendezetlen elemekkel – azaz n × (n-1)/2 .
• Válogatás nélküli elemekkel – a feltételezésnek megfelelően – majdnem annyi csere műveletünk van, mint elemekkel: például 4096 válogatás nélküli elemmel 4084 csere műveletünk van. Ezek a számok tesztről tesztre véletlenszerűen változnak.
• Viszont csökkenő sorrendbe rendezett elemekkel csak feleannyi swap-műveletünk van, mint elemünk! Ennek az az oka, hogy a csere során nemcsak a legkisebb elemet tesszük a megfelelő helyre, hanem a megfelelő cserepartnert is.

Nyolc elem esetén például négy csereoperációnk van. Az első négy iterációban egy-egy, az ötödiktől nyolcadikig tartó iterációkban pedig egy sem (ennek ellenére az algoritmus a végéig fut):

A mérésekből kiolvashatjuk továbbá:

• Az, hogy a Selection Sort miért olyan sokkal lassabb a csökkenő sorrendbe rendezett elemekkel, a legkisebb elem keresésekor a helyi változó hozzárendelések számában (minPos és min) keresendő. Míg 8192 rendezetlen elem esetén 69378 ilyen hozzárendelésünk van, csökkenő sorrendbe rendezett elemek esetén 16785407 ilyen hozzárendelés van – ez 242-szer annyi!

Miért ez a hatalmas különbség?

A legkisebb elem keresésének futási idejének elemzése

A csökkenő sorrendbe rendezett elemek esetén a nagyságrendet az iménti ábrából lehet levezetni. A legkisebb elem keresése a narancssárga és a narancssárga-kék dobozok háromszögére korlátozódik. A felső narancssárga részen az egyes dobozokban lévő számok egyre kisebbek, a jobb oldali narancssárga-kék részen a számok ismét növekednek.

A hozzárendelési műveletek minden narancssárga dobozban és a narancssárga-kék dobozok közül az elsőben történnek. A hozzárendelési műveletek száma minPos és min esetében tehát, képletesen szólva, körülbelül “a négyzet negyede” – matematikailag és pontosan ¼ n² + n – 1.

A rendezetlen elemek esetében sokkal mélyebbre kellene hatolnunk a dologban. Ez nemcsak ennek a cikknek, hanem az egész blognak a kereteit is meghaladná.

Ezért elemzésemet egy kis demóprogramra korlátozom, amely azt méri, hogy hány minPos/min hozzárendelés van, amikor a legkisebb elemet keressük egy rendezetlen tömbben. Íme az átlagos értékek 100 iteráció után (egy kis részlet; a teljes eredmény itt található):

n	átlagos minPos/min hozzárendelések száma
1.024	7.08
4.096	8.61
16.385	8.94
65.536	11.81
262.144	12.22
1.048.576	14.26
4.194.304	14.71
16.777.216	16.44
67.108.864	17.92
268.435.456	20.27

Itt mint egy diagram logaritmikus x-tengellyel:

A diagram nagyon szépen mutatja, hogy logaritmikus növekedésünk van, ill, az elemek számának minden megduplázódásával a hozzárendelések száma csak egy konstans értékkel nő. Mint mondtam, nem megyek bele mélyebben a matematikai háttérbe.

Ez az oka annak, hogy ezeknek a minPos/min hozzárendeléseknek a rendezetlen tömbökben nincs nagy jelentősége.

A Selection Sort egyéb jellemzői

A következő fejezetekben a Selection Sort térkomplexitását, stabilitását és párhuzamosíthatóságát fogom tárgyalni.

A Selection Sort térbonyolultsága

A Selection Sort térbonyolultsága állandó, mivel a i és j ciklusváltozókon, valamint a length, minPos és min segédváltozókon kívül nincs szükségünk további memóriahelyre.

Ez azt jelenti, hogy mindegy, hány elemet rendezünk – tíz vagy tízmillió -, mindig csak erre az öt további változóra van szükségünk. Az állandó időt O(1)-ként jegyezzük meg.

A kiválasztási rendezés stabilitása

A kiválasztási rendezés első pillantásra stabilnak tűnik: Ha a rendezetlen rész több azonos kulcsú elemet tartalmaz, akkor először az elsőt kell a rendezett részhez csatolni.

A látszat azonban csalóka. Ugyanis az algoritmus második allépésében két elem felcserélésével előfordulhat, hogy a rendezetlen rész bizonyos elemei már nem az eredeti sorrendben vannak. Ez viszont azt eredményezi, hogy a rendezett részben már nem az eredeti sorrendben jelennek meg.

Egy példa nagyon egyszerűen felépíthető. Tegyük fel, hogy van két különböző, 2. kulcsú és egy 1. kulcsú elemünk, amelyek a következőképpen vannak elrendezve, majd a Selection Sort segítségével rendezzük őket:

Az első lépésben az első és az utolsó elemet felcseréljük. Így a “KETTŐ” elem a “kettő” elem mögé kerül – a két elem sorrendje felcserélődik.

A második lépésben az algoritmus összehasonlítja a két hátsó elemet. Mindkettőnek ugyanaz a kulcsa, 2. Tehát egyetlen elem sem cserélődik.

A harmadik lépésben már csak egy elem marad; ezt automatikusan rendezettnek tekintjük.

A két 2 kulcsú elem tehát a kezdeti sorrendbe cserélődött – az algoritmus instabil.

A Selection Sort stabil változata

A Selection Sort úgy tehető stabilvá, hogy a második lépésben nem cseréljük fel a legkisebb elemet az elsővel, hanem az első és a legkisebb elem közötti összes elemet egy pozícióval jobbra toljuk, és a legkisebb elemet az elejére illesztjük.

Az időbonyolultság ugyan változatlan marad a változtatás miatt, de a további eltolások jelentős teljesítményromláshoz vezetnek, legalábbis ha tömböt rendezünk.

Hivatkozott listával a rendezni kívánt elem kivágása és beillesztése jelentős teljesítményveszteség nélkül elvégezhető lenne.

A kiválasztási rendezés párhuzamosíthatósága

A külső hurkot nem tudjuk párhuzamosítani, mert az minden iterációban megváltoztatja a tömb tartalmát.

A belső ciklus (a legkisebb elem keresése) párhuzamosítható a tömb felosztásával, az egyes altömbökben a legkisebb elem párhuzamos keresésével és a közbenső eredmények összevonásával.

Selection Sort vs. Insertion Sort

Melyik algoritmus a gyorsabb, a Selection Sort vagy az Insertion Sort?

Vetjük össze a Java implementációim méréseit.

A legjobb esetet kihagyom. Insertion Sort esetén a legjobb esetben az időbonyolultság O(n), és 524 288 elemig kevesebb mint egy ezredmásodpercig tartott. Tehát a legjobb esetben az Insertion Sort bármilyen elemszám esetén nagyságrendekkel gyorsabb, mint a Selection Sort.

n	Selection Sort unsorted	Insertion Sort unsorted	Selection Sort descending	Insertion Sort descending
…	…	…	…	…
16.384	27,9 ms	21,9 ms	65,6 ms	43,6 ms
32.768	108,0 ms	87,9 ms	265,4 ms	175,8 ms
65.536	434,0 ms	350,4 ms	1.052,2 ms	697,6 ms
131.072	1.729,8 ms	1.398,9 ms	4.209,9 ms	2.840,0 ms
262.144	6.913,4 ms	5.706,8 ms	16.863,7 ms	11.517,4 ms
524.288	27.649,8 ms	23.009,7 ms	67.537,8 ms	46.309,3 ms

És még egyszer diagramként:

Az Insertion Sort tehát nemcsak a legjobb esetben, hanem az átlagos és a legrosszabb esetben is gyorsabb a Selection Sortnál.

Az ok az, hogy az Insertion Sort átlagosan feleannyi összehasonlítást igényel. Emlékeztetőül: Insertion Sort esetén átlagosan a rendezett elemek felénél vannak összehasonlításaink és eltolásaink; Selection Sort esetén minden lépésben a legkisebb elemet kell megkeresnünk az összes rendezetlen elem között.

A Selection Sortnak lényegesen kevesebb írási művelete van, ezért a Selection Sort gyorsabb lehet, ha az írási műveletek drágák. Nem ez a helyzet a tömbökbe történő szekvenciális írásoknál, mivel ezek többnyire a CPU gyorsítótárában történnek.

A gyakorlatban ezért a Selection Sortot szinte soha nem használják.

Összefoglaló

A Selection Sort egy könnyen implementálható, és tipikus megvalósításában instabil rendezési algoritmus, amelynek átlagos, legjobb és legrosszabb esetben is O(n²) az időbonyolultsága.

A Selection Sort lassabb, mint az Insertion Sort, ezért a gyakorlatban ritkán használják.

A cikksorozat első részében az összes rendezési algoritmusról és azok jellemzőiről szóló áttekintésben további rendezési algoritmusokat találsz.

Ha tetszett a cikk, oszd meg bátran a cikk végén található megosztás gombok valamelyikével. Szeretne e-mailben értesülni, ha új cikket teszek közzé? Akkor az alábbi űrlap segítségével feliratkozhatsz a hírlevelemre.