Biográfia
Johannes Kepler ma elsősorban a bolygómozgás három, 1609-ben és 1619-ben közzétett törvényének felfedezéséről ismert.) Emellett fontos munkát végzett az optika területén (1604, 1611), felfedezett két új szabályos sokszöget (1619), először dolgozta fel matematikailag az egyenlő gömbök szoros egymásra helyezését (ami a méhsejtek alakjának magyarázatához vezetett, 1611), először bizonyította a logaritmusok működését (1624), és kidolgozott egy módszert a forgástestek térfogatának meghatározására, amely (utólag!) úgy tekinthető, hogy hozzájárult a számtan fejlődéséhez (1615, 1616). Ezenkívül kiszámította az eddig ismert legpontosabb csillagászati táblázatokat, amelyek folyamatos pontossága nagyban hozzájárult a heliocentrikus csillagászat igazságának megalapozásához (Rudolphin táblázatok, Ulm, 1627).
Kepler levelezésének nagy része fennmaradt. Számos levele szinte egy tudományos dolgozatnak felel meg (tudományos folyóiratok még nem léteztek), és úgy tűnik, hogy a levelezők azért őrizték meg őket, mert érdekesek voltak. Ennek következtében meglehetősen sokat tudunk Kepler életéről, sőt, jelleméről is. Részben ennek is köszönhető, hogy Kepler többé-kevésbé fiktív szereplőként futott be némi karriert (lásd a történetírói megjegyzést alább).
Gyermekkor
Kepler a svábországi Weil der Stadt kisvárosban született, és 1576-ban szüleivel a közeli Leonbergbe költözött. Apja zsoldos katona volt, anyja pedig egy fogadós lánya. Johannes volt az első gyermekük. Apja utoljára akkor hagyta el otthonát, amikor Johannes ötéves volt, és feltehetően a hollandiai háborúban halt meg. Gyermekkorában Kepler az anyjával a nagyapja fogadójában élt. Elmondása szerint a fogadóban felszolgálással segített. Elképzelhető, hogy a vendégeket néha zavarba ejtette a gyermek szokatlan számolási képessége.
Kepler korai tanulmányait egy helyi iskolában, majd egy közeli szemináriumban végezte, ahonnan felszentelési szándékkal a tübingeni egyetemre iratkozott be, amely akkor (és most is) a lutheri ortodoxia bástyája volt.
Kepler nézetei
Kepler egész életében mélyen vallásos ember volt. Minden írása számos utalást tartalmaz Istenre, és munkájában az Isten műveinek megértésére irányuló keresztény kötelességének teljesítését látta. Mivel az ember, ahogy Kepler hitte, Isten képmására teremtetett, nyilvánvalóan képes volt megérteni az általa teremtett világegyetemet. Kepler továbbá meg volt győződve arról, hogy Isten a világegyetemet egy matematikai terv szerint alkotta (ez a hit megtalálható Platón műveiben, és Pitagoraszhoz köthető). Mivel abban az időben általánosan elfogadott volt, hogy a matematika biztos módszert nyújt a világról szóló igazságokhoz való eljutáshoz (Euklidész általános fogalmait és posztulátumait ténylegesen igaznak tekintették), itt van egy stratégia az Univerzum megértésére. Mivel egyes szerzők Keplert irracionalitásnak nevezték, érdemes megjegyezni, hogy ez a meglehetősen reményteljes ismeretelmélet valóban nagyon messze áll a misztikus azon meggyőződésétől, hogy a dolgokat csak pontatlan módon lehet megérteni, amely az észnek nem alávetett felismerésekre támaszkodik. Kepler valóban többször is hálát ad Istennek, amiért megadja neki a meglátásokat, de a meglátásokat racionálisnak mutatja be.”
Egyetemi oktatás
Ebben az időben szokásos volt, hogy minden egyetemi hallgató “matematikai” kurzusokon vett részt. Ez elvileg magában foglalta a négy matematikai tudományt: a számtant, a geometriát, a csillagászatot és a zenét. Úgy tűnik azonban, hogy az, hogy mit tanítottak, az adott egyetemtől függött. Tübingenben Keplert a kor egyik vezető csillagásza, Michael Mästlin (1550-1631) tanította csillagászatra. A tantervben szereplő csillagászat természetesen a geocentrikus csillagászat volt, vagyis a ptolemaioszi rendszer aktuális változata, amelyben mind a hét bolygó – Hold, Merkúr, Vénusz, Vénusz, Nap, Mars, Jupiter és Szaturnusz – a Föld körül mozog, helyzetüket az állócsillagokhoz képest a körmozgások kombinálásával számították ki. Ez a rendszer többé-kevésbé összhangban volt a fizika jelenlegi (arisztotelészi) felfogásával, bár voltak bizonyos nehézségek, például az, hogy lehet-e “egyenletesnek” (és ezért nyilvánvalóan örökkévalónak elfogadhatónak) tekinteni egy olyan körmozgást, amely nem a saját középpontja, hanem egy másik pont (az úgynevezett “ekvantum”) körül zajlik egyenletesen. Úgy tűnik azonban, hogy a csillagászok (akik magukat “matematikusoknak” tekintették) összességében megelégedtek azzal, hogy folytassák a bolygók helyzetének kiszámítását, és a természetfilozófusokra bízták annak eldöntését, hogy a matematikai modellek megfelelnek-e a fizikai mechanizmusoknak. Kepler nem így állt hozzá. Legkorábbi publikált munkájában (1596) azt javasolja, hogy a bolygók tényleges pályáit vegyük figyelembe, ne pedig az azok megkonstruálásához használt köröket.
Tübingenben Kepler nemcsak matematikát, hanem görögöt és hébert is tanult (mindkettő szükséges a szentírások eredeti nyelven való olvasásához). A tanítás latinul folyt. Az első év végén Kepler a matematika kivételével mindenből ötöst kapott. Valószínűleg Mästlin azt akarta mondani neki, hogy jobbat is tudna, mert Kepler valójában azon kiválasztott tanulók közé tartozott, akiket kiválasztott arra, hogy a Kopernikusz új, heliocentrikus kozmológiai rendszerének megismertetésével haladóbb csillagászatot tanítson nekik. Mästlintől tudta meg Kepler, hogy a Forgásokról szóló előszó, amelyben kifejtette, hogy ez “csak matematika”, nem Kopernikusztól származik. Úgy tűnik, Kepler szinte azonnal elfogadta, hogy a kopernikuszi rendszer fizikailag igaz; az elfogadásának okait az első kozmológiai modelljével kapcsolatban tárgyaljuk (lásd alább).
Úgy tűnik, hogy már Kepler diákkorában is voltak arra utaló jelek, hogy vallási meggyőződése nem volt teljesen összhangban a Tübingenben uralkodó és a Confessio Augustana Ⓣ-ban megfogalmazott ortodox lutheranizmussal. Kepler problémái ezzel a protestáns ortodoxiával az anyag és a “szellem” (egy nem anyagi entitás) közötti feltételezett kapcsolatra vonatkoztak az Eucharisztia tanításában. Ez annyiban kapcsolódik Kepler csillagászatához, hogy nyilvánvalóan némileg hasonló intellektuális nehézségeket talált annak magyarázatában, hogy a Napból származó “erő” hogyan hathat a bolygókra. Írásaiban Kepler előszeretettel fekteti le a véleményét – ami a történészek számára nagyon kényelmes. A való életben valószínűnek tűnik, hogy a tübingeni hatóságok hasonló nyitottsága miatt a vallási ortodoxiával kapcsolatos megalapozott kétségek merültek fel a tübingeni hatóságok részéről. Ezek magyarázhatják, hogy Mästlin miért győzte meg Keplert, hogy hagyjon fel a felszentelési tervekkel, és helyette Grazban vállaljon matematikatanári állást. A vallási intolerancia a következő években tovább éleződött. Keplert 1612-ben kiátkozták. Ez sok fájdalmat okozott neki, de (akkor már) viszonylag magas társadalmi rangja ellenére, mint császári matematikusnak, soha nem sikerült elérnie a kitiltás feloldását.
Kepler első kozmológiai modellje (1596)
A hagyományos geocentrikus csillagászat hét bolygója helyett a kopernikuszi rendszerben csak hat volt, a Hold pedig a csillagászat számára korábban ismeretlen testté vált, amelyet Kepler később “műholdnak” nevezett (ezt az elnevezést 1610-ben alkotta meg a Galilei által felfedezett, a Jupiter körül keringő holdak leírására, szó szerinti jelentése “kísérő”). Miért hat bolygó?
A geocentrikus csillagászatban ráadásul nem volt mód arra, hogy megfigyelésekkel megállapítsák a bolygók egymáshoz viszonyított méretét; egyszerűen feltételezték, hogy érintkeznek egymással. Úgy tűnt, hogy ez nem szorul magyarázatra, mivel jól illeszkedett a természetfilozófusok azon meggyőződéséhez, hogy az egész rendszer a legkülső gömb mozgásától forog, egy (vagy talán kettő) a “fix” csillagok gömbjén túl (azokét, amelyek mintázata a csillagképeket alkotja), a Szaturnusz gömbjén túl. A kopernikuszi rendszerben az a tény, hogy az egyes bolygók mozgásának éves komponense a Föld éves mozgását tükrözte, lehetővé tette, hogy a megfigyelések alapján kiszámítsuk az egyes bolygók pályájának méretét, és kiderült, hogy a bolygók között hatalmas terek vannak. Miért éppen ezek a terek?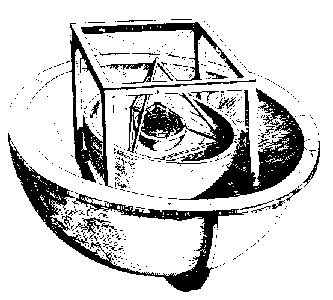
Kepler válasza ezekre a kérdésekre, amelyet Mysterium cosmographicum Ⓣ című művében (Tübingen, 1596) írt le, a huszadik századi olvasó számára bizarrnak tűnik (lásd a jobb oldali ábrát). Azt javasolta, hogy ha egy gömböt úgy rajzolnánk meg, hogy az érintse a Szaturnusz pályájának belsejét, és egy kockát írnánk bele, akkor a kockába írt gömb lenne a Jupiter pályáját körülíró gömb. Ha ezután egy szabályos tetraédert rajzolnánk a Jupiter pályáját beíró gömbbe, akkor a tetraéder belseje a Mars pályáját körülíró gömb lenne, és így tovább befelé, a Mars és a Föld közé a szabályos dodekaédert, a Föld és a Vénusz közé a szabályos ikozaédert, a Vénusz és a Merkúr közé pedig a szabályos oktaédert helyezve. Ez tökéletesen megmagyarázza a bolygók számát: csak öt konvex szabályos test létezik (amint azt Euklidész Elemek , 13. könyvében bizonyítottuk). Meggyőzően illeszkedik a Kopernikusz által levezetett pályák méretéhez is, a legnagyobb hiba kevesebb mint 10% (ami még most is látványosan jó egy kozmológiai modelltől). Kepler nem százalékos hibákban fejezte ki magát, és az övé valójában az első matematikai kozmológiai modell, de könnyen belátható, miért hitte, hogy a megfigyelési bizonyítékok alátámasztják az elméletét.
Kepler úgy látta, hogy kozmológiai elmélete bizonyítékot szolgáltat a kopernikuszi elmélet számára. Mielőtt saját elméletét bemutatta volna, érvekkel támasztotta alá magának a kopernikuszi elméletnek a hihetőségét. Kepler azt állítja, hogy előnye a geocentrikus elmélettel szemben a nagyobb magyarázó erejében rejlik. A kopernikuszi elmélet például meg tudja magyarázni, hogy a Vénusz és a Merkúr miért nem látható soha nagyon messze a Naptól (a Föld és a Nap között helyezkednek el), míg a geocentrikus elméletben nincs magyarázat erre a tényre. Kepler kilenc ilyen kérdést sorol fel a Mysterium cosmographicum Ⓣ első fejezetében.
Kepler ezt a munkát akkor végezte, amikor Grazban tanított, de a könyvet Mästlin Tübingenben látta át a sajtón. A megfigyelésekből levezetett értékekkel való egyezés nem volt pontos, és Kepler azt remélte, hogy a jobb megfigyelések javítani fogják az egyezést, ezért elküldte a Mysterium cosmographicum egy példányát a kor egyik legjelentősebb megfigyelő csillagászának, Tycho Brahe-nak (1546 – 1601). Tycho, aki akkoriban Prágában (a Szent Római Birodalom akkori fővárosában) dolgozott, valójában már írt Mästlinnek, hogy matematikai asszisztenst keres. Kepler kapta meg az állást.
A “háború a Marssal”
Naturális módon Tycho prioritásai nem egyeztek meg Kepler prioritásaival, és Kepler hamarosan a Mars pályájának megoldhatatlan problémáján találta magát. Tycho halála után (1601-ben) is folytatta a munkát, és Kepler követte őt a császári matematikusként. Hagyományosan a pályák körökből álltak össze, és meglehetősen kevés megfigyelési értékre volt szükség a körök relatív sugarainak és pozícióinak rögzítéséhez. Tycho rengeteg megfigyelést végzett, és Kepler elhatározta, hogy ezeket a lehető legjobban felhasználja. Lényegében olyan sok megfigyelés állt rendelkezésére, hogy ha egyszer megkonstruált egy lehetséges pályát, akkor azt további megfigyelésekkel tudta összevetni, amíg kielégítő egyezségre nem jutott. Kepler arra a következtetésre jutott, hogy a Mars pályája egy ellipszis, amelynek egyik gyújtópontjában a Nap áll (ezt az eredményt az összes bolygóra kiterjesztve ma “Kepler első törvényének” nevezik), és hogy a bolygót a Nappal összekötő vonal egyenlő idő alatt egyenlő területeket söpör ki, ahogy a bolygó leírja a pályáját (“Kepler második törvénye”), vagyis a területet az idő mértékeként használják. Miután ez a munka megjelent az Astronomia nova című folyóiratban, … Ⓣ, Heidelberg, 1609, Kepler a többi bolygóra is talált pályákat, és ezzel megállapította, hogy a két törvény rájuk is érvényes. Mindkét törvény a bolygó mozgását a Naphoz köti; Kepler kopernikanizmusa döntő jelentőségű volt érvelésében és következtetéseiben.
A Marsra vonatkozó számítások tényleges folyamata mérhetetlenül fáradságos volt – közel ezer fóliónyi számtani lap maradt fenn -, és Kepler maga úgy hivatkozik erre a munkára, mint “háborúm a Marssal”, de az eredmény egy olyan pálya lett, amely olyan pontosan megegyezik a modern eredményekkel, hogy az összehasonlításnál figyelembe kell venni a pálya Kepler kora óta bekövetkezett világi változásait.
Megfigyelési hiba
A lehetséges pályák megfigyelésekkel való összevetésének Kepler módszere szempontjából döntő fontosságú volt, hogy legyen elképzelése arról, hogy mit kell elfogadni megfelelő egyezésnek. Ebből ered a megfigyelési hiba fogalmának első kifejezett használata. Kepler ezt a fogalmat legalább részben Tychónak köszönhette, aki részletesen ellenőrizte műszerei teljesítményét (lásd Brahe életrajzát).
Optika és az 1604-es új csillag
A Marsról szóló munka 1605-re lényegében befejeződött, de a könyv kiadása késett. Közben a Hold látszólagos átmérőjének különbözőségével kapcsolatos aggodalmakra reagálva, amikor közvetlenül megfigyelték, és amikor camera obscura segítségével figyelték meg, Kepler az optikával kapcsolatos munkákat végzett, és előállt a camera obscura első helyes matematikai elméletével, valamint az emberi szem működésének első helyes magyarázatával, a retinán kialakuló, fejjel lefelé fordított képpel. Ezeket az eredményeket az Ad Vitellionem paralipomena, quibus astronomiae pars optica traditur Ⓣ című könyvében tette közzé, Frankfurt, 1604. Írt az 1604-es Új csillagról is, amelyet ma általában “Kepler szupernóvájának” neveznek, számos magyarázatot elutasítva, és egy helyen megjegyezte, hogy persze ez a csillag lehet, hogy csak egy különleges teremtés, “de mielőtt odajutnánk, azt hiszem, minden mást ki kell próbálnunk” De stella nova Ⓣ, Prága, 1606, 22. fejezet, KGW 1, 257. o., 23. sor.
Miután Galilei a távcső felhasználásával felfedezte a Jupiter holdjait, amit a Sidereal Messenger című művében (Velence, 1610) publikált, és amire Kepler lelkes választ írt (1610), Kepler tanulmányt írt a lencsék tulajdonságairól (az első ilyen optikai mű), amelyben bemutatta a távcső új konstrukcióját, két domború lencsét használva (Dioptrice, Prága, 1611). Ez a konstrukció, amelyben a végső kép fordított, olyan sikeres volt, hogy ma már általában nem Kepler-távcsőként, hanem egyszerűen csillagászati távcsőként ismerik.
Prága elhagyása Linzért
Kepler prágai évei viszonylag békésen teltek, és tudományos szempontból rendkívül termékenyek voltak. Sőt, még ha rosszul is mentek a dolgok, úgy tűnik, soha nem engedte, hogy a külső körülmények megakadályozzák abban, hogy folytassa a munkáját. A dolgok 1611 végén kezdtek nagyon rosszul alakulni. Először is, hétéves fia meghalt. Kepler azt írta egy barátjának, hogy ezt a halálesetet különösen nehezen viselte, mert a gyermek annyira emlékeztette őt saját magára ebben a korban. Aztán meghalt Kepler felesége. Ekkor Rudolf császár, akinek egészségi állapota megromlott, kénytelen volt lemondani testvére, Mátyás javára, aki Rudolfhoz hasonlóan katolikus volt, de (Rudolftól eltérően) nem hitt a protestánsokkal szembeni toleranciában. Keplernek el kellett hagynia Prágát. Távozása előtt átvitette felesége holttestét a fia sírjába, és latin sírfeliratot írt nekik. Megmaradt gyermekeivel Linzbe (ma Ausztriában) költözött.
Házasság és boroshordók
Kepler úgy tűnik, hogy első feleségét, Barbarát szerelemből vette feleségül (bár a házasságot egy közvetítőn keresztül intézte). A második, 1613-ban kötött házasságot gyakorlati szükségszerűség indokolta; szüksége volt valakire, aki vigyáz a gyerekekre. Kepler új felesége, Susanna, gyorstalpaló tanfolyamon ismerte meg Kepler jellemét: az ebből született könyv dedikáló levele kifejti, hogy az esküvői ünnepségen észrevette, hogy a boroshordók térfogatát egy átlósan a bordanyíláson át becsúsztatott rúd segítségével becsülték meg, és azon kezdett el tűnődni, hogyan működhet ez. Ennek eredménye lett a Nova stereometria doliorum … Ⓣ, Linz, 1615, a forgatható testek térfogatáról szóló tanulmány, amelyben Kepler Arkhimédész munkájára támaszkodva az “oszthatatlanokra” való felbontást alkalmazta. Ezt a módszert később Bonaventura Cavalieri (1598 körül – 1647) fejlesztette tovább, és az infinitezimális számítás ősei közé tartozik.
A világ harmóniája
Kepler fő feladata császári matematikusként az volt, hogy csillagászati táblázatokat írjon, Tycho megfigyelései alapján, de valójában A világ harmóniáját akarta megírni, amelyet 1599 óta tervezett A kozmosz misztériumának továbbfejlesztéseként. Ez a második kozmológiai mű (Harmonices mundi libri V Ⓣ, Linz, 1619) a korábbiaknál kidolgozottabb matematikai modellt mutat be, bár a poliéderek még mindig megvannak. A matematika ebben a műben tartalmazza a tesszellációk első szisztematikus kezelését, annak bizonyítását, hogy csak tizenhárom konvex egyenletes poliéder létezik (az archimédeszi testek), és az első beszámolót két nem konvex szabályos poliéderről (mindez a 2. könyvben). A világ harmóniája tartalmazza a ma már “Kepler harmadik törvényének” nevezett tételt is, amely szerint bármely két bolygó esetében a periódusaik négyzetének aránya megegyezik a pályáik átlagos sugarai kockáinak arányával. Kepler már az elsőtől kezdve olyan szabályt keresett, amely a pályák méretét a periódusokhoz kapcsolja, de e törvényhez nem vezetett lassú lépések sorozata, mint a másik kettőhöz. Valójában, bár a harmadik törvény fontos szerepet játszik A világ harmóniája nyomtatott változatának néhány utolsó szakaszában, valójában csak akkor fedezték fel, amikor a mű már nyomdában volt. Kepler az utolsó pillanatban végzett átdolgozásokat. Ő maga meséli el a végső siker történetét:
…és ha a pontos időpillanatra kíváncsiak vagytok, ez ezerhatszáztizennyolcadik év március 8-án fogant meg gondolatban, de szerencsétlen módon alávetette magát a számításnak, és ezért mint hamisat elvetette, és végül május 15-én visszatérve és új irányvonalat felvéve, megrohamozta elmém sötétségét. A Brahe megfigyelésein tizenhét éven át végzett munkám és a jelen tanulmány összeesküvése olyan erős támaszt nyújtott, hogy eleinte azt hittem, álmodom, és következtetésemet alaptételeim között feltételezem. De teljesen biztos és pontos, hogy “bármely két bolygó periodikus ideje közötti arány pontosan az átlagos távolságuk szeszkvalteres aránya…”
(Harmonice mundi 5. könyv, 3. fejezet, ford. Aiton, Duncan és Field, 411. o.).”
Boszorkányper
Amíg Kepler a Világ harmóniáján dolgozott, édesanyját boszorkánysággal vádolták meg. A tübingeni jogi kar segítségét vette igénybe. Katharina Keplert végül szabadon engedték, legalábbis részben technikai kifogások miatt, amelyek abból adódtak, hogy a hatóságok nem követték a megfelelő jogi eljárásokat a kínzás alkalmazása során. A fennmaradt dokumentumok hátborzongatóak. Kepler azonban tovább dolgozott. A hintóban, amikor Württembergbe utazott, hogy megvédje az anyját, elolvasta Vincenzo Galilei (1520 körül – 1591, Galileo apja) zeneelméleti művét, amelyre számos utalás található A világ harmóniájában.
Asztronómiai táblázatok
A táblázatok kiszámítása, egy csillagász szokásos tevékenysége, mindig nehéz számtannal járt. Kepler ennek megfelelően örömmel fogadta, amikor 1616-ban Napier logaritmusokról szóló (1614-ben megjelent) munkájára bukkant. Mästlin azonban azonnal közölte vele, hogy egyrészt illetlenség egy komoly matematikustól, hogy egy egyszerű számítási segédeszköznek örüljön, másrészt pedig, hogy nem bölcs dolog megbízni a logaritmusokban, mert senki sem érti, hogyan működnek. (Hasonló megjegyzéseket tettek a számítógépekkel kapcsolatban is az 1960-as évek elején.) Kepler válasza a második ellenvetésre az volt, hogy egy kifogástalanul hiteles forrásból származó bizonyítást tett közzé a logaritmusok működéséről: Euklidész Elemek 5. könyve. Kepler kiszámította a nyolcjegyű logaritmusok táblázatait, amelyeket a Rudolphine Tables (Ulm, 1628) című művében tett közzé. A csillagászati táblázatok nemcsak Tycho megfigyeléseit, hanem Kepler első két törvényét is felhasználták. Minden olyan csillagászati táblázat, amely új megfigyeléseket használt fel, a kiadást követő első néhány évben pontos volt. A Rudolphin-táblázatokban az volt a figyelemre méltó, hogy évtizedeken át pontosnak bizonyultak. És ahogy gyűltek az évek, a táblázatok folyamatos pontosságát természetesen a Kepler-törvények helyessége, és így a heliocentrikus csillagászat helyessége melletti érvnek tekintették. Azzal, hogy Kepler teljesítette unalmas hivatalos feladatát császári matematikusként, legkedvesebb vágya teljesült: segített a kopernikanizmus megalapozásában.
Wallenstein
A Rudolphi táblázatok megjelenésekor Kepler valójában már nem a császárnak dolgozott (1626-ban távozott Linzből), hanem Albrecht von Wallensteinnek (1583 – 1632), a harmincéves háború (1618 – 1648) kevés sikeres katonai vezetőjének egyikének.
Wallenstein, akárcsak Rudolf császár, Keplertől várta az asztrológián alapuló tanácsokat. Keplernek természetesen engedelmeskednie kellett, de többször hangsúlyozza, hogy szerinte nem lehet pontos jóslatokat készíteni. Mint a kor legtöbb embere, Kepler is elfogadta az asztrológia elvét, miszerint az égitestek befolyásolhatják a Földön történő eseményeket (a legvilágosabb példa erre, hogy a Nap okozza az évszakokat, a Hold pedig az árapályokat), de kopernikuszi gondolkodásúként nem hitt a csillagképek fizikai valóságában. Az ő asztrológiája csak az égitestek helyzete közötti szögeken (“asztrológiai aspektusok”) alapult. Teljes megvetését fejezi ki a hagyományos asztrológia bonyolult rendszerei iránt.
Halál
Kepler Regensburgban halt meg, rövid betegség után. A városban tartózkodott, amikor úton volt, hogy begyűjtse a Rudolphin táblázatokkal kapcsolatban neki járó pénzt. A helyi templomban temették el, de ez a harmincéves háború során elpusztult, és a sírból nem maradt semmi.
Historiográfiai megjegyzés
Kepler tudományos tevékenységének állítólag nem racionális elemeiről néha sokat beszéltek. A hívő asztrológusok gyakran állítják, hogy munkássága tudományosan tekintélyes előzményt nyújt a sajátjukhoz. A néhai Arthur Koestler nagy hatású Alvajárók című művében Kepler és a Mars csatáját a modern tudomány eredendő irracionalitása melletti érvvé tette. E két meggyőződésnek sok hallgatólagos követője akadt. Mindkettő azonban Kepler művének nagyon részleges olvasatán alapul. Különösen úgy tűnik, hogy Koestler nem rendelkezett a Kepler eljárásainak megértéséhez szükséges matematikai szakértelemmel. A közelebbi tanulmányozás azt mutatja, hogy Koestler egyszerűen tévedett az értékelésében.
A valóban fontos nem racionális elem Kepler munkájában a kereszténysége. Kepler a matematika széleskörű és sikeres használata miatt munkája “modernnek” tűnik, de valójában egy keresztény természetfilozófussal van dolgunk, aki számára az Univerzum természetének megértése magában foglalta a Teremtő természetének megértését is.