A meredekség-intercept formában az egyenletet így írjuk fel:
$$y=mx+b$$$
Ahol m az egyenes meredeksége és b az y-intercept. Ezt az egyenletet használhatod egyenlet felírására, ha ismered a meredekséget és az y-interceptust.
Példa
Keresd meg az egyenes egyenletét
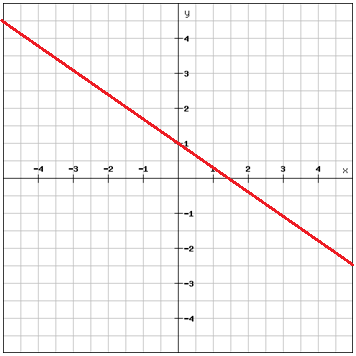
Válassz két pontot, amelyek az egyenesen vannak
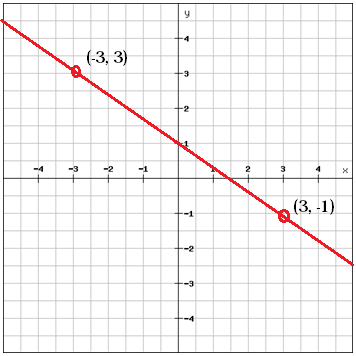
Kalkuláld ki a két pont közötti meredekséget
$$m=\frac{y_{2}\, -y_{1}}{x_{2}\, -x_{1}}=\frac{\left (-1 \right )-3}{3-\left ( -3 \right )}=\frac{-4}{6}=\frac{-2}{3}$$
Megtalálhatjuk a b-értéket, az y-interceptust, ha megnézzük a grafikont
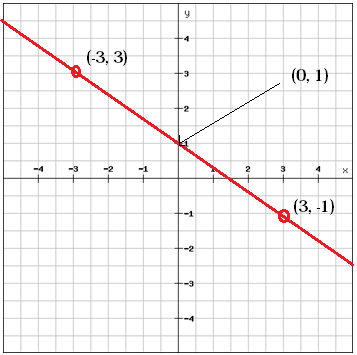
b = 1
Megtaláltuk m értékét és b értékét. Így megkapjuk a lineáris függvényt
$$y=-\frac{2}{3}x+1$$
Sok esetben a b értéke nem olvasható le ilyen könnyen. Ezekben az esetekben, vagy ha bizonytalanok vagyunk abban, hogy az egyenes valóban keresztezi-e az y-tengelyt az adott pontban, kiszámíthatjuk b-t úgy, hogy megoldjuk a b egyenletét, majd x és y helyettesítjük a két pont valamelyikével.
A fenti példával szemléltethetjük ezt. Megvan a két pont (-3, 3) és (3, -1). Ebből a két pontból kiszámítottuk a meredekséget
$$m=-\frac{2}{3}$$$
Ez adja az egyenletet
$$y=-\frac{2}{3}x+b$$$
Ez alapján megoldhatjuk az egyenletet b-re
$$b=y+\frac{2}{3}x$$$
És ha az első pontunkból származó értékeket (-3, 3), akkor
$$b=3+\frac{2}{3}\cdot \left ( -3 \right )=3+\left ( -2 \right )=1$$
Ha ezt a b értéket beírjuk az egyenletbe, akkor
$$y=-\frac{2}{3}x+1$$$
mely ugyanaz az egyenlet, mint amit akkor kaptunk, amikor az y-interceptust olvastuk le a grafikonról.
A lineáris egyenlet felírásának összefoglalása a meredekség-intercept forma segítségével
- Meghatározzuk a meredekséget, m. Ezt úgy tehetjük meg, hogy a meredekségi képlet segítségével kiszámítjuk az egyenes két ismert pontja közötti meredekséget.
- Megkeressük az y-interceptet. Ezt úgy lehet megtenni, hogy a meredekséget és az egyenes egy pontjának (x, y) koordinátáit behelyettesítjük a meredekség-metszet képletbe, majd megoldjuk b-re.
Ha már megvan m és b is, akkor egyszerűen beírhatjuk őket az egyenletbe a megfelelő helyükre.
Videolecke
Keresd meg a grafikon egyenletét
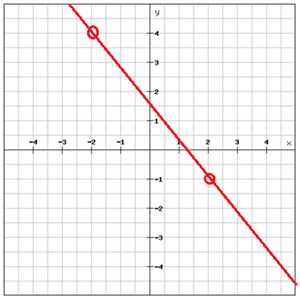
.