Kondenzátor alapok, a kondenzátorok működése és különböző típusai, valamint alkalmazásuk az áramkörökben

Kondenzátorok – a szó mintha a kapacitás gondolatát sugallná, ami a szótár szerint “valaminek a befogadóképességét” jelenti. A kondenzátor pontosan ezt teszi – elektromos töltést tart. De mitől lesz ez szinte minden elektronikus áramkörben gyakori alkatrész? Bontsuk le a kondenzátorok mögötti dolgokat, hogy megértsük, mit csinál, és hogyan lehet használni őket ebben a cikkben.

Mi a kondenzátor?

A kondenzátor a legprimitívebb formában két vezető lemezből áll, amelyeket egy dielektromos közeg választ el egymástól. A dielektrikum kifejezés csak egy divatos szó egy olyan szigetelőre, amely polarizálható, azaz ellentétes felületeken negatív és pozitív töltéseket képezhet. Amikor feszültséget kapcsolunk a két lemezen, áram folyik a vezető lemezeken keresztül. Az egyik oldal pozitívan töltődik (elektronhiány), a másik oldal pedig negatívan töltődik (elektronfelesleg). Mindannyian ismerjük azt a tényt, hogy az ellentétes töltések vonzzák egymást, így mivel a lemezek ellentétesen töltöttek, a lemezeken lévő töltések vonzzák egymást.

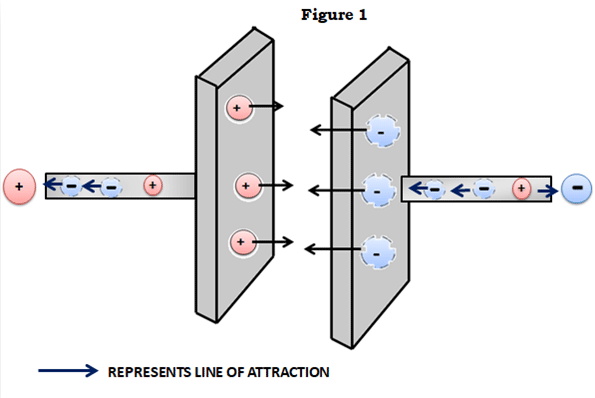
Ne feledjük, hogy a lemezek között szigetelő van, így a töltések nem tudnak “áramolni”, hogy kiegyenlítsék egymást, és (ideális esetben) a kölcsönös vonzás állapotában megrekednek és helyben maradnak. És így látják el a kondenzátorok a legalapvetőbb funkciójukat – a töltés megtartását vagy tárolását.

A kondenzátorok szimbóluma

Mivel a kondenzátorok két párhuzamos fémlemezzel rendelkeznek, mint fentebb tárgyaltuk, a szimbólumuk is mintegy ugyanazt jelképezi. Legalábbis könnyű lerajzolni

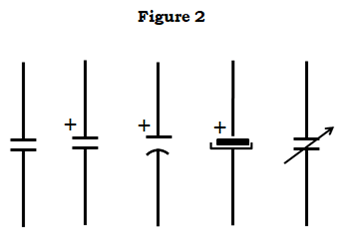
A gyakorlati esetben a kondenzátorok már nem csak két lemezből állnak, amelyek között rés van, az alumínium elektrolitok esetében a két lemez egy csőbe tekert fémfólia formáját ölti, amelyek között egy távtartó van.

A második szimbólumcsoport a polarizált kondenzátorokat jelöli, vagyis azokat, amelyeknek belső kialakításukkal meghatározott pozitív és negatív pólusuk van. Ha véletlenül felcseréljük ezeket a pólusokat, az szinte biztosan látványos meghibásodáshoz vezet (különösen a nagyobb példányok esetében), a hiba helyéről fóliadarabok és papírméterek dobódnak ki, és legtöbbször nagyon rossz szagúak.

Kapacitás és feszültségérték egy kondenzátor esetében

A kondenzátorokat Faradban mérik; a nevet a híres brit elektrokémikus, Michael Faraday után kapta. A kapacitás mértékegysége, a Coulomb per Volt helyett áll. A Coulomb (ejtsd: “koo-lom”) a töltés S.I. egysége, a Volt pedig, mint tudjuk, a feszültség vagy potenciálkülönbség egysége. A Farad tehát az egy Volt potenciálkülönbségre jutó tárolt töltés mennyisége. A kondenzátor matematikai szemléletének ez az egyszerű módja sokféle értelmezésre ad lehetőséget, ami sok halálosan bonyolult matematikai egyenletben, például integrálokban, exponensekben és vektorokban nyilvánul meg, amelyeket mi, mérnökök használunk a kondenzátorokkal való munka során, ami túlmutat ennek a cikknek a keretein. A cikk későbbi részében azonban belemegyünk egy kis érdekes matematikába, amely segít nekünk a kondenzátorokkal való áramkörök tervezésében

A Farad (egy Coulomb per Volt) természetesen a legtöbb gyakorlati célra nagyon nagy egység (mivel maga a Coulomb elég nagy töltésmennyiség, mint azt már talán tudod), ezért a legtöbb kondenzátort (a nagyon nagyok kivételével) mikrofaradban, vagyis a Farad egymilliomod részében (0,000001) mérik. Tegyük fel, hogy van egy kondenzátorod, aminek a műanyag külső borításán 25V 10uF van feltüntetve (az “u” előtag a mikrot jelenti, ez a görög µ (“mu”) jel “mikro” jelentésű alakja). Mivel a sapka (az elektronika világában a kondenzátorok rövidítése) 10uF-ra van méretezve, a csatlakozóin átmenő feszültség tíz mikrocoulomb (azaz a Coulomb tízmilliomod része, 0,000010 C) töltést képes megtartani minden egyes voltra. Ez azt jelenti, hogy a maximális 25 V-os feszültségnél a kondenzátor 25 V x 10uF töltést képes megtartani, ami 0,000250 Coulombnak felel meg.

Memlékezzünk, hogy “maximális” feszültséget mondtam. A maximális feszültség valószínűleg a kondenzátoron lévő legfontosabb jelölés. Megmutatja, hogy a kondenzátor mekkora feszültséget tud kezelni a kapcsain, mielőtt KABOOM………!

A kondenzátor működése

A kondenzátorban alapvetően az történik, hogy a lemezek közötti szigetelő a “dielektromos átütés” nevű folyamaton megy keresztül, ami azt jelenti, hogy a szigetelő már nem tud szigetelni, mivel a feszültség a szigetelőn túl magas ahhoz, hogy szigetelő maradhasson. A mögöttes fizika némiképp nem tartozik a tárgyhoz, de ahhoz, hogy megértsük, miért történik ez, csak annyit kell tudnunk, hogy egyetlen szigetelő sem tökéletes, vagyis egy bizonyos pontig. Még a legerősebb híd is összeomlik, ha túlterhelődik. Ami itt történik, az hasonló. Az összeomlás csökkentése érdekében növelheti a két lemez közötti rést, de ez kompromisszummal jár – csökkentett kapacitással, mivel a lemezek távolabb vannak egymástól, és a töltések nem vonzzák annyira, mint amikor közelebb vannak – hasonlóan ahhoz, ahogy a mágnesek viselkednek.

A jó ökölszabály az lenne, hogy 50%-kal nagyobb feszültségre méretezett sapkákat használjon, mint amire az áramköre várhatóan számíthat. Ez nagy biztonsági tartalékot hagy. Például, ha egy sapkára van szüksége egy 12V-os tápegység sínjének leválasztásához (ne aggódjon, a leválasztást később a cikkben elmagyarázzuk), akkor megúszhatja egy 16V-os kondenzátor használatával, de egy 25V-os kondenzátor használata ajánlott, mivel ez széles biztonsági tartalékot biztosít. Oké, rájöttél!!! Igen, a 25V természetesen nem 25%-kal nagyobb, mint a 12V, de a 18V nem egy szabványos kondenzátorérték – nem fogsz találni ilyen feszültségű kondenzátort. A legközelebbi 25V.

A kondenzátorok különböző típusai

Az átütési feszültségtartományok oka a dielektrikumként használt anyag, ami alapján a kondenzátorokat is osztályozzák:

Alumínium elektrolitikus kondenzátorok

Ezek talán a legfelismerhetőbb kondenzátortípusok. Jellegzetes fémdobozokban, műanyag burkolattal, egyértelműen megadott feszültség- és kapacitásértékekkel, valamint a katódot jelző fehér sávval kerülnek forgalomba. A név onnan ered, hogy a “lemezek”, mint már említettük, kémiailag maratott alumíniumfóliából készülnek. A maratási eljárás porózussá teszi az alumíniumot (hasonlóan a szivacshoz), és nagymértékben megnöveli a felületét, ezáltal növeli a kapacitást. A dielektrikum egy vékony alumínium-oxid réteg. Ezeket a kondenzátorokat olajjal töltik meg, amely elektrolitként viselkedik, innen a név. Az elektrolitikus kondenzátorok belső felépítésük miatt polarizáltak. A kondenzátorcsalád többi tagjához képest nagy kapacitással rendelkeznek, de sokkal alacsonyabb feszültséggel. Számíthat arra, hogy az elektrolitok 0,1uF és 100mF közötti szörnyek, mint 100mF között és néhány voltos névleges feszültséggel körülbelül 500V-ig terjedő névleges feszültségekkel találkozhat. Belső ellenállásuk azonban általában magas.

MÁSODIK MEGJEGYZÉS: A kondenzátorok belső ellenállása annak az anyagnak köszönhető, amelyből a kondenzátor készült – például az alumíniumfólia ellenállása vagy a vezetékek ellenállása.

Kerámia kondenzátorok

Ezek a kondenzátorok kerámia dielektrikummal rendelkeznek. Mivel a kerámia dielektrikum átütési határa meglehetősen magas, számíthat arra, hogy őrült átütési feszültségű, például 10 kV-os átütési feszültségű kerámia sapkákkal találkozhat. A kapacitások azonban általában alacsonyak, a pikofarádok (0,0000000000000001F) és a mikrofarádok néhány tízes tartományában. Általában sokkal kisebbek, mint más típusú kondenzátorok, amint az a képen látható. Nagyon kis belső ellenállással is rendelkeznek.

Kerámia kondenzátorok azonosítása

A kerámia kondenzátor kapacitásának értéke nem lesz közvetlenül feltüntetve a kerámia kondenzátoron. Mindig lesz egy háromjegyű szám, amelyet egy változó követ; tanuljuk meg, hogyan azonosíthatjuk az értéket e számok segítségével. Tekintsük a következő kondenzátort.

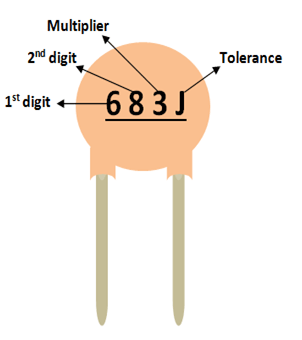
Amint észrevehetjük, ez a három számjegy két számjegyre oszlik, a harmadik pedig a szorzó. Ebben az esetben a 68 a számjegy, a 3 pedig a szorzó. Tehát a 68-at meg kell szorozni 10^3-mal. Egyszerűen fogalmazva ez 68, amit 3 nulla követ. Ezért ennek a kondenzátornak az értéke 68000 pF lesz. Vegye figyelembe, hogy az egységnek mindig pF-nek kell lennie. Hasonlóképpen a 220 kóddal ellátott kondenzátor azt jelenti, hogy 22 Pico farad, mivel 10^0 az 0.

A kondenzátor névleges feszültségét a kód alatti sor segítségével lehet megtalálni. Ha van vonal, akkor a feszültség értéke 50/100V, ha nincs vonal, akkor 500V.

A leggyakrabban használt kondenzátorértékek, valamint azok Pico Faradban, Nano Faradban és mikrofaradban történő átalakítása az alábbiakban található.

Filmkondenzátorok

Amint a neve is mutatja, ezekben a kondenzátorokban a dielektrikum egy műanyag film, gyakran ismerős műanyagok, például mylar és poliészter. Ugyanazokkal a tulajdonságokkal rendelkeznek, mint a kerámia sapkák, magas átütési feszültségekkel (a műanyag polimerek viselkedése miatt) és alacsony kapacitásokkal. Az egyetlen különbség az, hogy általában valamivel nagyobbak, bár felületesen úgy néznek ki, mint a kerámia sapkák. Belső ellenállásuk a kerámiakapcsokhoz hasonló.

Tantál és nióbium kondenzátorok

Ezek a sapkák technikailag a kondenzátorok elektrolitikus kategóriájába tartoznak. Itt az elektrolit egy tantál- vagy nióbium-oxidokból álló szilárd anyag. Adott kapacitáshoz képest nagyon alacsony belső ellenállással rendelkeznek, azonban más típusokhoz képest (a kerámia a legjobb) kevésbé védettek a túlfeszültséggel szemben, és hajlamosak különösebb figyelmeztetés nélkül, csúnya fekete füsttel tönkremenni.

Speciális célú kondenzátorok

Ezek közé tartoznak az ezüst – csillámsapkák, X és Y névleges sapkák stb. Az X és Y névleges kondenzátorokat például vezetékszűrésre építik – robusztusabb konstrukció és nagyobb névleges feszültség, valamint alacsony kapacitások, hogy csökkentsék a rajta áthaladó áramot, ha váltakozó feszültséget alkalmaznak, és korlátozzák a kupakban tárolt energiát, ha egyenfeszültséget alkalmaznak.

Superkondenzátorok és ultrakondenzátorok

Ezek a kondenzátorokat egy teljesen új szintre emelik, nagymértékben megnövelt kapacitásokkal, néha több száz Farad tartományban! Ez néhány ügyes kémiai eljárásnak köszönhetően lehetséges. A szuperkondenzátorok és az ultrakondenzátorok áthidalják a kondenzátorok és a kémiai akkumulátorok közötti szakadékot. Ezek azonban nagyon alacsony feszültségűek.

És ezek nagyjából az összes olyan gyakori kondenzátortípus, amellyel az elektronika világában általában találkozhatunk.

Hogyan viselkednek a kondenzátorok az áramkörökben

Az első hasznos feladat az lenne, ha megtanulnánk, hogyan kell kiszámítani a kondenzátorban tárolt energiát, amit a következő képlet ad meg,

E = 1/2CV2

Ahol E a tárolt energia Joule-ban, C a kapacitás Faradban, V pedig a feszültség Voltban. Figyeljük meg, hogy ez az egyenlet sok más newtoni energiaegyenlet formáját veszi fel, egy csinos húsvéti tojás!

Tegyük fel, hogy van egy 50V feszültségre méretezett sapkánk, amelynek kapacitása 1000uF, akkor a tárolt energia a teljes 50V mellett:

1/2 * 0.001000F * 50V * 50V * 50V

Azt jelenti, hogy a tárolt energia mínusz 1,25J.

Ez feltárja a kondenzátorok, mint energiatároló eszközök egyik legnagyobb hátrányát – a tárolt energia egy adott mérethez képest nagyon alacsony, egy ugyanolyan méretű akkumulátor legalább ezerszer több tárolt energiával rendelkezne! A kondenzátoroknak azonban jóval kisebb a belső ellenállása, mint a kémiai akkumulátoroknak, ami lehetővé teszi, hogy az összes tárolt energiát gyorsan leadják. Egy akkumulátor rövidre zárása csak felmelegedést okozna a belső ellenállás által elvezetett energia miatt, de egy kondenzátor rövidre zárása csak néhány szikrát hozna létre, mivel az összes töltés egyszerre ürül ki a kondenzátor károsodása nélkül.

Második, van egy másik szép képlet, amely a feszültséget, az áramot és a kapacitást kapcsolja össze:

I/C = dV/dt

Ahol I a kondenzátorba táplált áram amperben, C a kapacitás Faradban és dV/dt a kondenzátor kapcsain lévő feszültség változásának sebessége. Gondoljon ennek egységére – adott áram és kapacitás esetén a másodpercenkénti voltra. Ne aggódjon a kis “d” miatt, ez csak egy matematikai módja annak, hogy “a határérték nulla”.

Tegyük fel, hogy van egy tápegységünk, amely állandó 5V-os feszültséget ad ki 1mA állandó áram mellett, akkor az egyenlet átrendezésével megtalálhatjuk az időt, ami egy 100uF-os kondenzátor 5V-ra töltéséhez szükséges:

dt = CdV/I

dt = (0.000100F * 5V)/0,001A

dt = 0,5 másodperc

Így a kondenzátor 0,5 másodperc alatt töltődne fel 5V-ra. (Ne feledjük, hogy egy kondenzátor csak a hozzá táplált maximális feszültségig képes töltődni, soha többre, nem tudnak varázslatos módon feszültséget “létrehozni”.)

A kondenzátornak ez a kiszámítható viselkedése nagyon hasznossá teszi például időbeli késleltetések generálására, egy kis kiegészítő áramkörrel. Az egyenletet átrendezhetjük, hogy időt kapjunk.

Most jöjjön a jó dolog – tényleges kondenzátoros áramkörök!

Kondenzátorok viselkedése áramkörökben

Kezdjük egyszerűen – a kondenzátorok különböző összekapcsolási módjaival. Ez nagyjából ugyanaz, mint két ellenállás összekapcsolása – vagy sorba vagy párhuzamosan kapcsolhatjuk őket.

Kondenzátorok párhuzamosan

A lenti ábrán három kondenzátor párhuzamosan van összekötve, a megfelelő pozitív és negatív csatlakozókkal együtt (feltételezve, hogy a kondenzátorok polarizáltak). Ennek az elrendezésnek a teljes kapacitása egyszerűen az áramkörben lévő összes kondenzátor összes kapacitásának összege. Ennek van értelme, mivel a kondenzátorlemezek párhuzamos összekapcsolása növeli a felületet, ami növeli a kapacitást.

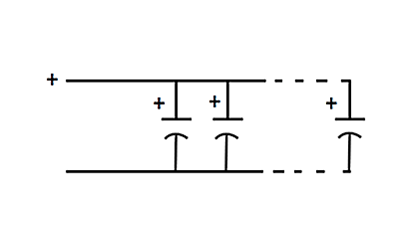
A maximális feszültség, amit egy ilyen elrendezés elbír, a legkisebb kondenzátor feszültsége, mivel a feszültségben az összes kupak közös.

Egy példának kell ezt tisztáznia. Tegyük fel, hogy van két kondenzátorod, az egyiknek a névleges értéke 25V 470uF, a másiké 35V 1000uF. A teljes kapacitás 470uf + 1000uF = 1470uF lenne. Azonban a maximális feszültség, amelyet erre a bankra (egy csomó egymáshoz kapcsolt kondenzátort kondenzátor-“banknak” nevezhetünk), csak 25V lenne. Ha ennél nagyobb értéket tennél erre a bankra, szikrákat szórnál, mivel túllépnéd a 25V-os kondenzátor maximális feszültségét.

Kondenzátorok sorba kapcsolása

A kondenzátorok párhuzamos kapcsolása különösen akkor hasznos, ha nagy kapacitást akarsz, és csak kis értékekkel rendelkezel. Ha ezeket a kisebb értékű kupakokat párhuzamosan összeilleszted, akkor végül megkapod a nagyobb értéket, és elvégzed a feladatot, feltéve, hogy figyelsz a feszültségre.

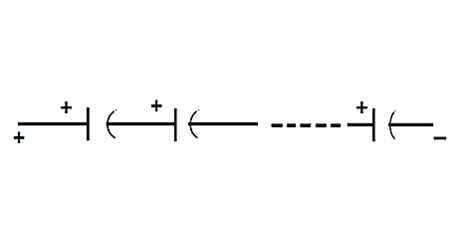
A kondenzátorok sorba kötése már egy kicsit bonyolultabb. A kapacitást a képlet adja meg:

1/Ctotal = 1/C1 + 1/C2 + … + 1/Cn

Ahol C1, C2…Cn az áramkörben használt egyes kondenzátorok kapacitása.

A bank által most kezelhető feszültség a névleges feszültségek összege.

Ha kapunk egy 10V 1uF névleges feszültségű és egy 50V 10uF névleges feszültségű kondenzátort, akkor a feszültség, amit a bank sorban kezelni tud, 10V + 50V = 60V. A kapacitás értéke 0,9091uF.

Kondenzátor feszültsége az idő függvényében

Mi van akkor, ha egy kondenzátort szeretnénk tölteni? Egyszerűen csatlakoztathatjuk egy feszültségforráshoz, mint az alábbi ábrán. Itt az történne, hogy abban a pillanatban, amikor a feszültségforrást csatlakoztatjuk, feltételezve, hogy a kondenzátor teljesen lemerült, a töltések rohamtempóban felhalmozódnak a lemezeken, ami egy nagyon nagy (elméletileg végtelen!) áramsugarat eredményez, amelyet csak a kondenzátor belső ellenállása korlátoz. Ez természetesen nem kívánatos, ha az áramforrásod történetesen valami olyan, mint egy akkumulátor. Egy ésszerű ötlet az lenne, ha a kondenzátorral és a feszültségforrással sorba kapcsolna egy ellenállást, hogy korlátozza az áramot, mint az ábrán, és voila! Van valami, amit a mérnökök RC áramkörnek neveznek, “R” az ellenállásért és “C” a kondenzátorért!

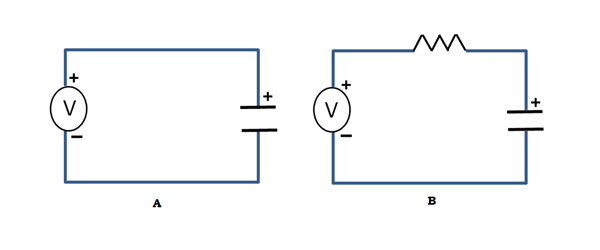
Ez az áramkör érdekes viselkedést mutat. Amikor a feszültséget az ellenállás ‘I’ jelű oldalára kapcsoljuk, a kondenzátoron lévő feszültség lassan emelkedik, mivel az áram korlátozott. A grafikon valahogy így néz ki:

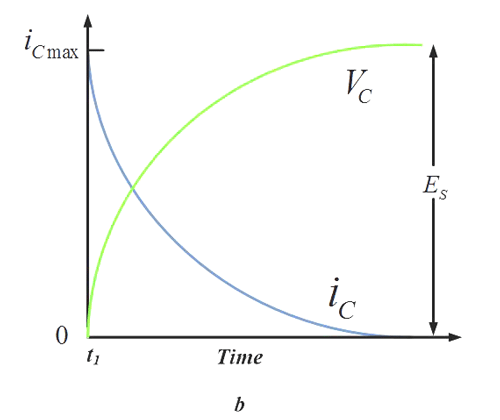
A matematikailag hajlamosabb nézőim felismerik a meredekség alakját – hasonlít az exponenciális függvényhez!

Emlékszel, hogy azt mondtam, hogy a sapkákat időbeli késleltetések létrehozására lehet használni? Ez az egyik módja annak, hogy ezt állandó áramforrás nélkül (amihez további áramkörökre van szükség). Mivel egy adott feszültség eléréséhez szükséges idő kiszámítható, ha ismerjük a kapacitást, a feszültséget és az ellenállást, létrehozhatunk időkésleltetési áramköröket.

Az ellenállás és a kapacitás szorzatát, RC-t, az áramkör időállandójának nevezzük. Ez a paraméter akkor válik hasznossá, ha valóban pontosan meg akarjuk határozni az adott feszültség eléréséhez szükséges időt, amint azt az alábbi grafikon ábra mutatja.

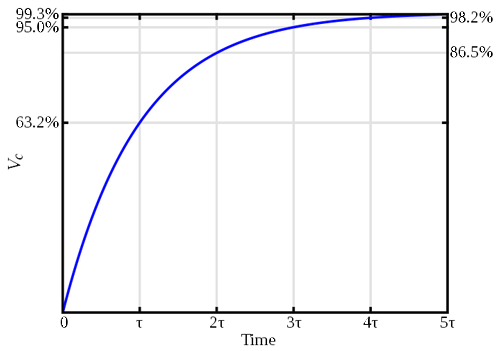
A grafikonból látható, hogy a kondenzátor egy időállandó alatt eléri az alkalmazott feszültség 63%-át, és így tovább.

Ezt az elvet használja az 555-ös időzítő minden évszakban, bár a tervezési egyenletek kissé eltérőek.

Az RC-áramkörök másik érdekes alkalmazása a jelszűrés, azaz a nem kívánt frekvenciájú elektromos jel eltávolítása az áramkörből. Az RC áramkörnek egy adott időre van szüksége ahhoz, hogy feltöltődjön és kisüljön egy forrásból. Ha egy periodikus hullámot alkalmazunk, amelynek időperiódusa nagyobb, mint az RC, akkor ugyanaz a jel nagyon kis torzítással jelenik meg a kimeneten. A frekvencia növelésével azonban a jel folyamatosan gyorsabban változtatja a polaritást, mint ahogy az áramkör tölteni és kisütni képes, és végül egy bizonyos pont után a jel eltűnik, és csak tiszta egyenáram marad! Ezt hívják jelcsillapításnak. Mint látható, egy RC áramkör úgy működik, mint egy szűrő, amely egy bizonyos frekvencián túl blokkolja az AC jeleket (még az egyenáramúakkal szuperponált, azaz egyenáramú eltolással rendelkező jeleket is). Ezt a fajta szűrőt aluláteresztő szűrőnek nevezzük, azaz alacsony frekvenciákat átenged, de magas frekvenciákat nem enged át.

Kondenzátorok váltakozó áramú áramkörökben

A kondenzátorok érdekes módon viselkednek, ha váltakozó áramú áramkörökbe helyezzük őket. A jel szempontjából frekvenciafüggő ellenállásokként gondolhatunk rájuk. Mint fentebb láttuk, az RC-áramkör minden váltakozó áramot blokkol a jelből, de mi történik, ha egy kondenzátort sorba kapcsolunk egy váltakozó áramú feszültségforrással? Pontosan az ellenkezője!

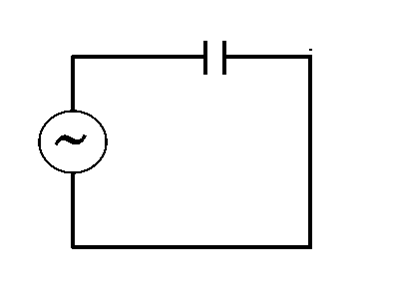
Mivel a kondenzátor csak két fémlemez, amelyeket egy szigetelő választ el egymástól, nem enged át rajta egyenáramot. Egy váltóáramú jel azonban állandóan változó feszültséggel rendelkezik, így az egyik lemez változó feszültséget lát, és a másik lemezen ellentétes töltést indukál, ahogy az ábrán látható:

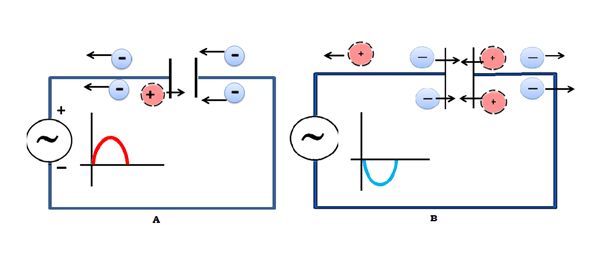
Ez összességében azt eredményezi, hogy viszonylag magas frekvenciákon áramot “enged át” a kondenzátoron. A kimenettel párhuzamosan egy ellenállás hozzáadásával egy magántompító szűrő jön létre, azaz egy olyan szűrő, amely csak a magas frekvenciákat engedi át, és minden egyenáramú jelet blokkol.

A kondenzátor “váltakozóáramú ellenállását” vagy impedanciáját a következő képlet adja meg:

XC = 1/(2*π*f*C)

Ahol XC a kapacitív reaktancia vagy impedancia, f a frekvencia és C a kapacitás. Ezt a képletet használhatja a kondenzátor virtuális “ellenállásának” kiszámításához egy váltakozó áramkörben.

Hol találhatók kondenzátorok a természetben

Oké, ennyi elég volt az elméletből. Nézzük meg a kondenzátorok sokféle felhasználási módját.

Az első hely, ahol várhatóan kondenzátorokkal találkozhatunk, mindenféle tápegységekben van szűrőként és leválasztásként. Töltéstartályként működnek – gyors áramot biztosítanak, amikor a terhelésnek szüksége van rá.

Itt van két oszcilloszkópos felvétel, amelyek azt mutatják, milyen hatása van annak, ha nincs és ha van egy kondenzátor a tápegység vezetékein keresztül. Mint látható, a kondenzátorok megléte drámaian csökkenti a tápegység sínjeinek “zaját”, így védve a kényes alkatrészeket a hirtelen feszültségcsúcsoktól.

Azokat “leválasztó” kondenzátoroknak is nevezik, mivel “leválasztják” az áramkör azon részeit a tápegységről, amelyeken át vannak szerelve. Előfordulhat, hogy egy áramköri lapon a tápvezetékek elég hosszúak, és nagy induktivitással és ellenállással rendelkeznek. Ez ahhoz vezethet, hogy a szokásosnál kevesebb áramot szolgáltatnak. Ha a tápvezeték végén van egy kondenzátor, az olyan, mintha egy kisebb ideiglenes “akkumulátor” lenne az eszközön keresztül, amely szükség esetén kitörő áramot biztosít, és feltöltődik, amikor az eszköz kevés energiát fogyaszt.

A tápegység csatlakozóinak “hullámzó” feszültségének eltávolításához szükséges kapacitás kiszámításához az I/C = dV/dt képletet használhatja.

Tegyük fel, hogy van egy olyan tápegységed, amelynek feszültsége 10ms-enként 11,5V és 12V között változik (hullámzás), ami az 50Hz-es frekvencia miatt gyakori a hálózati tápellátású eszközöknél, és a feszültség kiegyenlítése érdekében egy sapkát kell elhelyezned a csatlakozókon. Ha a terhelési áram ebben az esetben 1A, akkor a képletet így rendezhetjük át, hogy megtudjuk a kapacitást:

(I * dt)/dV

Hol I a terhelési áram, dt a zaj időperiódusa, és dV a hullámzó feszültség. Az értékeket behelyettesítve azt találjuk, hogy 20000uF kapacitásra van szükségünk. Most ez soknak tűnhet, de sokkal kevesebbel is megúszhatja. A kapott érték csak iránymutatásul szolgál.

A valós életben többféle típusú és értékű kondenzátorral találkozhat a tápnyomvonalakon, ez azért van, hogy a zajtartalmat sok frekvencián keresztül csökkentsük, és a lehető legsimább feszültséget kapjuk.

A kondenzátorok másik felhasználása bonyolult szűrőkben van, mint például ez:

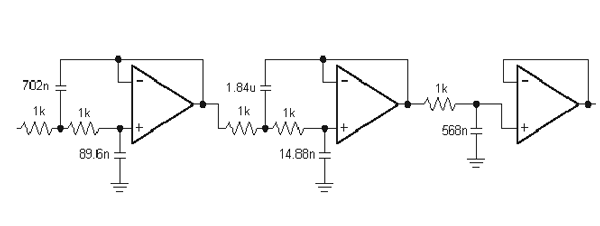
De egy egyszerűbb szűrő lenne az RC-szűrő, egy érdekes szűrő itt van leírva.

Mindenki ismeri az Arduino mikrokontroller táblát. Sokoldalú eszköz, de nem gondolkodott még soha azon, hogy az analóg kimenetek miért köpnek ki egy digitális PWM jelet? Ez azért van, mert úgy tervezték őket, hogy egy külső szűrőhálózattal használják őket, hogy a PWM feszültséget valóban analóg feszültséggé simítsák. Ezt olyan egyszerű alkatrészekkel lehet elvégezni, mint egy 1K ellenállás és egy 10uF kondenzátor. Próbálja ki!

Egy másik felhasználási mód, mint fentebb említettük, az időzítés. Egy egyszerű oszcillátor építhető egy NAND kapu (próbáljuk meg kitalálni, miért nem működnek az AND kapuk), egy ellenállás és egy kondenzátor segítségével.

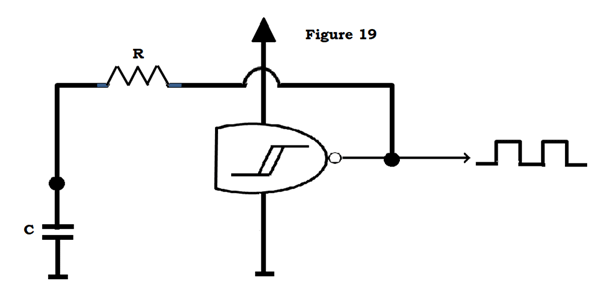
Feltéve, hogy kezdetben nincs feszültség a kondenzátoron, a NAND bemenetek (amelyek össze vannak kötve) közel 0V-ot látnak rajtuk, és bekapcsolják a kimenetet. A sapka most az ellenálláson keresztül töltődik fel. Amikor eléri a kapu “magas” küszöbértékét, a kimenet alacsonyra vált, és a kupak most kisül. Ez a ciklus folytatódik, hogy négyszöghullámú kimenetet hozzon létre, amelynek frekvenciája az R és C értékétől függ.

Végül, a kondenzátorok másik érdekes felhasználása az energiatárolás. Természetesen a kondenzátorok nem felelnek meg az akkumulátoroknak, de bizonyos alkalmazásokhoz, amelyeknek gyorsan kell az energia, a kupakok a legjobbak a feladatra.

Az olyan eszközöknek, mint a tekercspuskák (több található az interneten), nagy áramimpulzusra van szükségük a lövedék felgyorsításához, ezért ilyen célokra nagyfeszültségű kondenzátorokat használnak, gyakran olyan névleges értékekkel, mint a 450V 1500uF, amelyek jelentős mennyiségű energiát képesek tárolni.