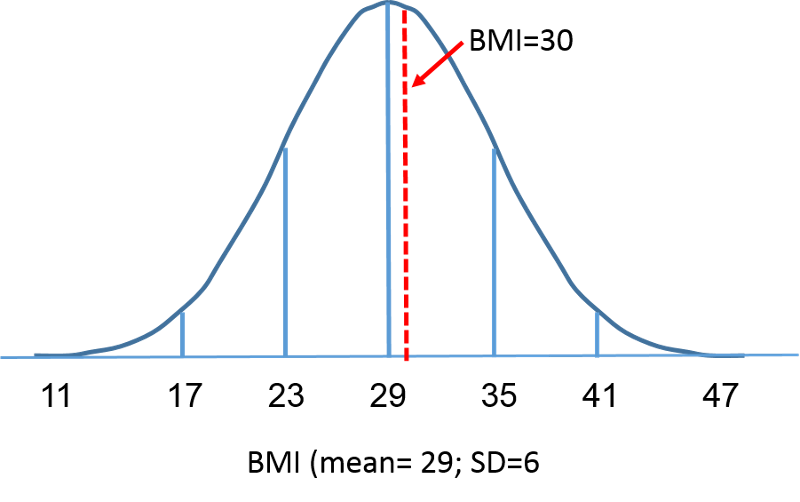
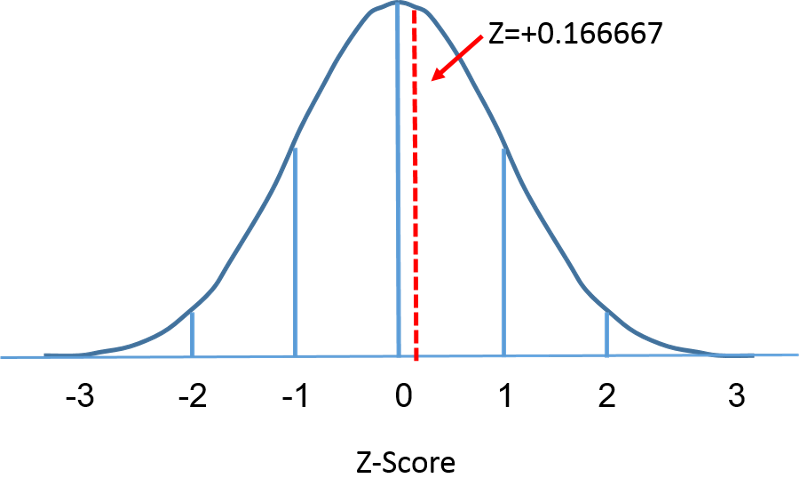
A standard normális eloszlás olyan normális eloszlás, amelynek átlaga nulla, szórása pedig 1. A standard normális eloszlás középpontja nulla, és azt, hogy egy adott mérés mennyire tér el az átlagtól, a szórás adja meg. A standard normális eloszlás esetén a megfigyelések 68%-a az átlagtól 1 szóráson belül van; 95%-a az átlagtól 2 szóráson belül van; és 99,9%-a az átlagtól 3 szóráson belül van. Eddig a pontig az “X”-et használtuk az érdekes változó jelölésére (pl. X=BMI, X=magasság, X=súly). A standard normális eloszlás használatakor azonban a “Z”-t fogjuk használni a változóra való utaláshoz a standard normális eloszlás kontextusában. A standardizálás után az előző oldalon tárgyalt BMI=30 alább látható, amely 0,16667 egységgel fekszik a jobb oldali standard normális eloszlás 0-as átlaga felett.
 ====
====
Mivel a standard görbe alatti terület = 1, elkezdhetjük pontosabban meghatározni az egyes megfigyelések valószínűségeit. Bármely adott Z-pontszámhoz kiszámíthatjuk a Z-pontszámtól balra lévő görbe alatti területet. Az alábbi keretben lévő táblázat a standard normális eloszlás valószínűségeit mutatja. Vizsgálja meg a táblázatot, és vegye figyelembe, hogy a 0,0 “Z” pontszám 0,50 vagy 50%-os valószínűséget, az 1 “Z” pontszám pedig 0,8413 vagy 84%-os valószínűséget jelent, ami egy szórással az átlag felett van. Ez azért van így, mert az átlag feletti és alatti egy standard eltérés a terület körülbelül 68%-át foglalja magában, így az átlag feletti egy standard eltérés a 34% felét jelenti. Tehát az átlag alatti 50% plusz az átlag feletti 34% adja a 84%-ot.
A Z standard normális eloszlás valószínűségei
![]()
Ez a táblázat úgy van megszervezve, hogy megadja a görbe alatti területet egy megadott értéktől balra vagy annál kisebbre vagy “Z-érték”. Ebben az esetben, mivel az átlag nulla, a szórás pedig 1, a Z-érték az átlagtól való szórásegységek száma, a terület pedig az adott Z-értéknél kisebb érték megfigyelésének valószínűsége. Figyeljük meg azt is, hogy a táblázat a Z két tizedesjegyig mutatja a valószínűségeket. A bal oldali oszlopban az egységek helye és az első tizedesjegy látható, a második tizedesjegy pedig a felső soron keresztül.
De térjünk vissza a kérdéshez, amely arra a valószínűségre vonatkozik, hogy a BMI kisebb, mint 30, azaz P(X<30). Erre a kérdésre a standard normális eloszlás segítségével tudunk válaszolni. Az alábbi ábrák a 60 éves férfiak BMI-eloszlását és a standard normális eloszlást mutatják egymás mellett.
A BMI eloszlása és a standard normális eloszlás
 ====
====
A görbe alatti terület mindkét esetben egy, de az X tengely skálázása eltérő. Figyeljük meg azonban, hogy a szaggatott vonaltól balra eső területek megegyeznek. A BMI eloszlása 11 és 47 között mozog, míg a standardizált normális eloszlás, Z, -3 és 3 között mozog. Ki akarjuk számítani a P(X < 30) értéket. Ehhez meghatározhatjuk az X = 30-nak megfelelő Z értéket, majd a fenti standard normális eloszlási táblázat segítségével megkereshetjük a valószínűséget vagy a görbe alatti területet. A következő képlet egy X értéket Z-értékké, más néven standardizált értékké alakít át:

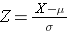
ahol μ az X változó átlaga és σ a szórás.
A P(X < 30) kiszámításához az X=30-at a megfelelő Z pontszámra alakítjuk át (ezt nevezzük standardizálásnak):

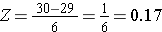
Ezért P(X < 30) = P(Z < 0,17). Ezután megnézhetjük a standard normális eloszlási táblázatból ennek a Z-pontszámnak a megfelelő valószínűségét, amely azt mutatja, hogy P(X < 30) = P(Z < 0,17) = 0,5675. Így annak a valószínűsége, hogy egy 60 éves férfi BMI-je 30-nál kisebb, 56,75%.
Másik példa
A BMI-re ugyanezt az eloszlást használva, mennyi annak a valószínűsége, hogy egy 60 éves férfi BMI-je 35-nél nagyobb? Más szóval, mekkora a P(X > 35)? Ismét standardizálunk:

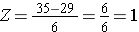
Most a standard normális eloszlás táblázatában megnézzük a P(Z>1) értéket, és Z=1,00 esetén azt találjuk, hogy P(Z<1,00) = 0,8413. Megjegyezzük azonban, hogy a táblázat mindig annak a valószínűségét adja meg, hogy Z kisebb a megadott értéknél, azaz P(Z<1)=0,8413.
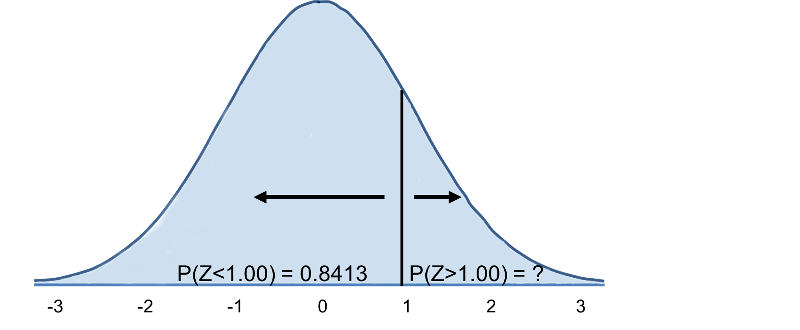
Ezért P(Z>1)=1-0,8413=0,1587. Értelmezés: A 60 éves férfiak csaknem 16%-ának 35 feletti a BMI-je.
Normális valószínűségszámító
![]()
![]()
Z-pontszámok R-rel
A normális valószínűségek táblázatban való keresése vagy az Excel használata helyett az R segítségével is kiszámíthatjuk a valószínűségeket. Például,
> pnorm(0)
Egy 0 értékű Z-pontszám (bármely eloszlás átlaga) 50%-a balra van. Mennyi annak a valószínűsége, hogy a fenti populációban egy 60 éves férfinak a BMI-je 29-nél (az átlag) kisebb? A Z-pontszám 0 lenne, és pnorm(0)=0,5 vagy 50%.
Mi a valószínűsége annak, hogy egy 60 éves férfinak 30-nál kisebb a BMI-je? A Z-pontszám 0,16667.
> pnorm(0,16667)
Így a valószínűség 56,6%.
Mi a valószínűsége annak, hogy egy 60 éves férfi BMI-je 35-nél nagyobb lesz?
35-29=6, ami egy standard eltéréssel az átlag felett van. Tehát kiszámíthatjuk a balra eső területet
> pnorm(1)
és az eredményt kivonjuk 1,0-ból
1-0,8413447= 0,1586553
Azt a valószínűséget, hogy egy 60 éves férfi BMI-je nagyobb legyen 35-nél, 15,8%-nak tekintjük.
Vagy az R segítségével egyetlen lépésben kiszámolhatjuk az egészet a következőképpen:
> 1-pnorm(1)
Valószínűség egy értéktartományra

Mi a valószínűsége annak, hogy egy 60 éves férfi BMI értéke 30 és 35 között van? Vegyük észre, hogy ez ugyanaz, mintha azt kérdeznénk, hogy a 60 éves férfiak mekkora hányadának van 30 és 35 közötti BMI-je. Pontosabban azt szeretnénk, hogy P(30 < X < 35)? Korábban kiszámítottuk a P(30<X) és a P(X<35) értékeket; hogyan lehet ezt a két eredményt felhasználni annak a valószínűségnek a kiszámításához, hogy a BMI 30 és 35 között lesz? Próbáld meg önállóan megfogalmazni és megválaszolni, mielőtt megnéznéd az alábbi magyarázatot.
Válasz