
A növények képesek spirálisan új sejteket növeszteni, mint például a magok mintája ebben a gyönyörű napraforgóban.
A spirál természetesen történik, mert minden új sejt egy fordulat után keletkezik.
“Új sejt, majd fordulat,
majd egy másik sejt, majd fordulat, …”
Hogyan forduljunk?
Szóval, ha növény lennél, mennyit fordulnál az új sejtek között?
Ha egyáltalán nem fordulsz, akkor egyenes vonal lesz.
![]()
De ez egy nagyon rossz tervezés ….valami kereket akarsz, ami hézagmentesen összetart.
Miért nem próbálod megkeresni a számodra legjobb értéket?
Kipróbálj különböző értékeket, például 0,75, 0,9, 3,1416, 0,62 stb.
Emlékezz arra, hogy az elejétől a végéig hézagmentes mintát próbálsz létrehozni:
(Egyébként nem számít az egész számrész, mint az 1. vagy az 5., mert ezek teljes fordulatszámok, amelyek ugyanabba az irányba mutatnak vissza.)
Mit kaptál?
Ha olyasmit kaptál, aminek a vége 0,618 (vagy 0,382, ami 1 – 0,618), akkor “Gratulálunk, a növényvilág sikeres tagja vagy!”
 |
Ez azért van, mert az aranymetszés (1.61803…) a legjobb megoldás, és a napraforgó a maga természetes módján rájött erre. Kipróbáld … így kell kinéznie. |
Miért?
Minden olyan szám, amely egyszerű tört (például: 0.75 az 3/4, és 0,95 az 19/20, stb.) egy idő után olyan mintázatot fog alkotni, amelyben a vonalak egymásra rakódnak, ami hézagokat képez.
De az aranymetszés (szimbóluma a görög Phi betű, balra látható) szakértője annak, hogy ne legyen semmilyen tört.
Ez egy irracionális szám (ami azt jelenti, hogy nem tudjuk egyszerű törtként leírni), de ennél is több … a lehető legtávolabb van attól, hogy bármilyen tört közelében legyen.
| Az, hogy irracionális, még nem elég | |
|---|---|
 |
Pi (3.141592654…), ami szintén irracionális. Egy tizedesjegye sajnos nagyon közel van az 1/7-hez (= 0,142857…), így 7 karral végződik. |
 |
e (2,71828…).) szintén irracionális, szintén nem működik, mert a tizedesjegye közel van az 5/7-hez (0,714285…), így ez is 7 karral végződik. |
Hogyan működik tehát az aranymetszés?
| Az aranymetszés egyik különleges tulajdonsága, hogy önmagában is meghatározható, így: | |
| (Számokban: 1,61803… = 1 + 1/1,61803….) | |
| Ez kibővíthető ezzel az örökké tartó törttel (amit “folytatódó törtnek” nevezünk): | |
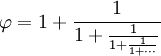 |
|
Ez tehát szépen becsúszik az egyszerű törtek közé.
Fibonacci-számok
Az aranymetszés és a Fibonacci-számok között különleges kapcsolat van (0, 1, 1, 1, 2, 3, 5, 8, 13, 21, … stb, minden szám az előtte lévő két szám összege).
Ha bármelyik két egymást követő (egymás utáni) Fibonacci-számot vesszük, arányuk nagyon közel áll az aranymetszéshez:
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
2
|
3
|
1.5 | |
|
3
|
5
|
1.666666666… | |
|
5
|
8
|
1.6 | |
|
8
|
13
|
1.625 | |
|
13
|
21
|
1.615384615… | |
|
…
|
…
|
… | |
|
144
|
233
|
1.618055556… | |
|
233
|
377
|
1.618025751… | |
|
…
|
…
|
… |

Így, ahogy természetesen hét kart kapunk, ha 0.142857 (1/7), hajlamosak vagyunk Fibonacci-számokat kapni, amikor az aranymetszést használjuk.
Próbáld meg megszámolni a spirálkarokat – a “balra forduló” spirálokat, majd a “jobbra forduló” spirálokat … milyen számokat kaptál?
Spirális levélnövekedés

Ez az érdekes viselkedés nem csak a napraforgómagokban található meg.
A levelek, ágak és szirmok is képesek spirálisan növekedni.
Miért? Azért, hogy az új levelek ne takarják el a napot az idősebb levelek elől, vagy azért, hogy a lehető legtöbb eső vagy harmat jusson le a gyökerekhez.
Tény, hogy amikor egy növénynek spirálja van, a forgás általában két egymást követő (egymás utáni) Fibonacci-számmal alkotott tört, például:
- A fél forgás 1/2 (1 és 2 Fibonacci-számok)
- A 3/5 is gyakori (mindkettő Fibonacci-szám), és
- 5/8 is (kitaláltad!)
mind egyre közelebb kerül az aranymetszéshez.
|
És ezért a Fibonacci-számok nagyon gyakoriak a növényekben. Itt egy százszorszép 21 szirommal |
 |
De ezt nem minden növénynél látjuk, hiszen a természetben sokféle módszer van a túlélésre.
Az aranyszög
Az eddigiekben “fordulatokról” (teljes elfordulásokról) beszéltünk.
A 0,61803… fordulat egyenértéke 222,4922… fok, vagyis körülbelül 222,5°.
A másik irányban ez körülbelül 137,5°, amit “aranyszögnek” nevezünk.
Amikor tehát legközelebb a kertben sétálsz, keresd az aranyszöget,
és számold a szirmokat és a leveleket, hogy megtaláld a Fibonacci-számokat,
és felfedezd, milyen okosak a növények … !
gyakorlat
Mi lenne, ha most rögtön kimennél a kertbe vagy a parkba, és elkezdenéd számolni a leveleket és a szirmokat, és mérni a forgásokat, hogy lásd, mit találsz.
Eredményeidet felírhatod erre az űrlapra:
| Növény neve vagy leírása: | |||
| Spirálisan nőnek a levelek? Y / N | |||
| Számolj meg egy levélcsoportot: | |||
| Hány levél (a) ? | |||
| Hány teljes fordulat (b) ? | |||
| Felületenkénti forgás (b/a) : | |||
| Forgási szög (360 × b/a) : | |||
| Vannak virágok? Y / N | |||
| Hány szirom van az 1. virágon: | |||
| Virág 2: | |||
| Virág 3: | |||
(De ne feledjük, a természetnek megvannak a maga szabályai, és nem kell követnie a matematikai mintákat,
de amikor igen, akkor félelmetes látni.)
* Megjegyzések az animációról
A napraforgómagok a középpontból kifelé nőnek, de az animáción egyszerűbbnek találtam, hogy először a fiatalabb magokat rajzoljam meg, és hozzáadjam az idősebbeket.
Az animációnak tovább kellene folytatódnia, hogy ugyanolyan legyen, mint a napraforgó – ez 55 spirált eredményezne az óramutató járásával megegyezően és 34 spirált az óra járásával ellentétesen (egymást követő Fibonacci-számok). Csak nem akartam, hogy túl sokáig tartson.
A spirálok nincsenek beprogramozva – természetes módon keletkeznek, amikor megpróbáljuk a magokat a lehető legközelebb helyezni egymáshoz, miközben a megfelelő forgásirányban tartjuk őket.

