Valintalajittelu – Algoritmi, lähdekoodi, aikakompleksisuus

Tämä artikkeli on osa sarjaa ”Lajittelualgoritmit: Ultimate Guide” ja…

• kuvaa, miten Selection Sort toimii,
• sisältää Selection Sortin Java-lähdekoodin,
• näyttää, miten sen aikakompleksisuus saadaan selville (ilman monimutkaista matematiikkaa)
• ja tarkastaa, vastaako Java-toteutuksen suorituskyky odotettua ajonaikaista käytöstä.

Koko artikkelisarjan lähdekoodi löytyy GitHub-arkistostani.

Esimerkki: Pelikorttien lajittelu

Pelikorttien lajittelu käteen on klassinen esimerkki Insertion Sortista.

Selection Sortia voidaan havainnollistaa myös pelikorteilla. En tunne ketään, joka poimii korttejaan tällä tavalla, mutta esimerkkinä se toimii ihan hyvin 😉

Aluksi asetat kaikki korttisi kuvapuoli ylöspäin pöydälle eteesi. Etsit pienimmän kortin ja otat sen kädestäsi vasemmalle. Sitten etsit seuraavaksi suuremman kortin ja laitat sen pienimmän kortin oikealle puolelle, ja niin edelleen, kunnes lopulta otat suurimman kortin aivan oikealle.

Ero Insertion Sort -lajitteluun

Insertion Sort -lajittelussa otimme seuraavaksi lajittelemattoman kortin ja laitoimme sen oikeaan paikkaan lajiteltujen korttien joukossa.

Selection Sort -lajittelussa toimitaan tavallaan toisin päin: Valitsemme lajittelemattomista korteista pienimmän kortin ja sitten – yksi toisensa jälkeen – lisäämme sen jo lajiteltuihin kortteihin.

Selection Sort Algorithm

Algoritmi voidaan selittää yksinkertaisimmin esimerkin avulla. Seuraavissa vaiheissa näytän, miten joukko lajitellaan Selection Sortilla:

Vaihe 1

Jakaamme joukon vasempaan, lajiteltuun osaan ja oikeaan, lajittelemattomaan osaan. Lajiteltu osa on alussa tyhjä:

Vaihe 2

Haemme pienintä elementtiä oikeasta, lajittelemattomasta osasta. Tätä varten muistamme ensin ensimmäisen elementin, joka on 6. Siirrymme seuraavaan kenttään, josta löydämme vielä pienemmän elementin 2. Käymme läpi loputkin osajoukosta etsien vielä pienempää elementtiä. Koska emme löydä sellaista, pysymme elementissä 2. Asetamme sen oikeaan paikkaan vaihtamalla sen ensimmäisenä olevaan elementtiin. Sitten siirretään matriisin osien rajaa yhden kentän verran oikealle:

Vaihe 3

Etsimme jälleen oikeasta, lajittelemattomasta osasta pienintä elementtiä. Tällä kertaa se on 3; vaihdamme sen toisena olevaan elementtiin:

Vaihe 4

Etsimme jälleen pienintä elementtiä oikeasta osasta. Se on 4, joka on jo oikeassa paikassa. Tässä vaiheessa ei siis tarvita vaihto-operaatiota, vaan siirretään vain jakson rajaa:

Vaihe 5

Pienimmäksi elementiksi löydetään 6. Vaihdamme sen oikean osan alussa olevaan elementtiin 9:

Vaihe 6

Kahdesta jäljelle jäävästä elementistä 7 on pienin. Vaihdetaan se 9:ään:

Algoritmi valmis

Viimeinen elementti on automaattisesti suurin ja siten oikeassa asemassa. Algoritmi on valmis, ja elementit on lajiteltu:

Valintalajittelu Javan lähdekoodi

Tässä osiossa on yksinkertainen Java-toteutus valintalajittelusta.

Ulkoinen silmukka iteroi lajiteltavien elementtien yli, ja se päättyy toiseksi viimeisen elementin jälkeen. Kun tämä elementti on lajiteltu, myös viimeinen elementti lajitellaan automaattisesti. Silmukkamuuttuja i osoittaa aina oikeanpuoleisen, lajittelemattoman osan ensimmäiseen elementtiin.

Kussakin silmukkasyklissä oikeanpuoleisen osan ensimmäiseksi elementiksi oletetaan aluksi pienin elementti min; sen sijainti tallennetaan minPos.

Sisäinen silmukka iteroi sitten oikean osan toisesta alkioelementistä sen loppuun ja määrittää min ja minPos uudelleen aina, kun löydetään vielä pienempi alkioelementti.

Sisäisen silmukan päätyttyä asemien i (oikean osan alku) ja minPos alkioelementit vaihdetaan toisiinsa (elleivät ne ole sama alkio).

public class SelectionSort { public static void sort(int elements) { int length = elements.length; for (int i = 0; i < length - 1; i++) { // Search the smallest element in the remaining array int minPos = i; int min = elements; for (int j = i + 1; j < length; j++) { if (elements < min) { minPos = j; min = elements; } } // Swap min with element at pos i if (minPos != i) { elements = elements; elements = min; } } }}

Näytetty koodi eroaa GitHub-arkistossa olevasta SelectionSort-luokasta siten, että se toteuttaa SortAlgorithm-rajapinnan, jotta se on helposti vaihdettavissa testikehyksen sisällä.

Valintalajittelun aikamäärän monimutkaisuus

Merkitsemme n:llä elementtien lukumäärää, esimerkissämme n = 6.

Kahden sisäkkäisen silmukan avulla saamme selville sen, että aikamäärän monimutkaisuus* on O(n²). Näin on, jos molemmat silmukat iteroivat arvoon, joka kasvaa lineaarisesti n:n kanssa.

Se on ilmeisesti totta ulomman silmukan kohdalla: se laskee n-1:een asti.

Entä sisempi silmukka?

Katsokaa seuraavaa kuvaa:

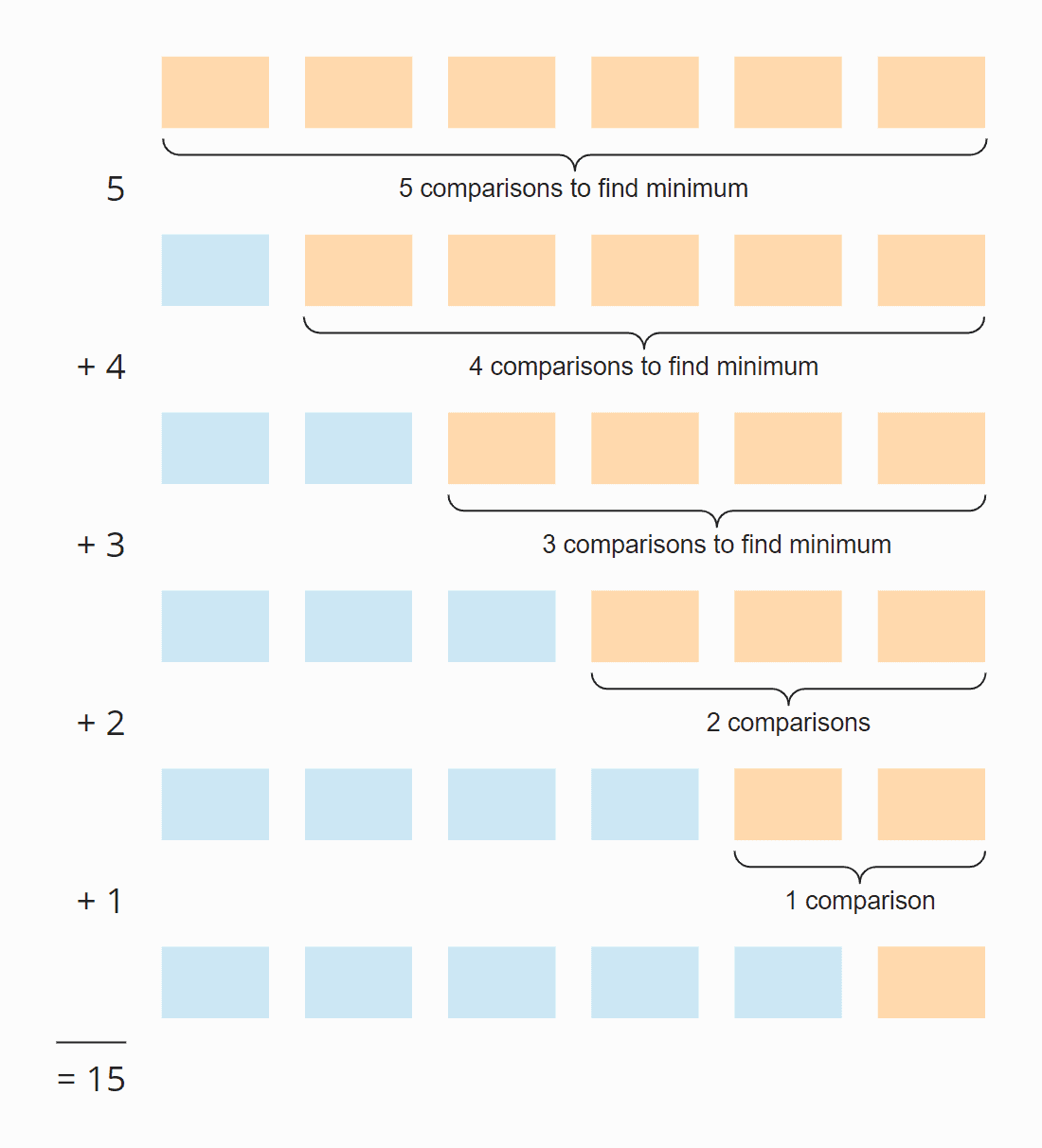
Joka askeleella vertailujen määrä on yksi vähemmän kuin lajittelemattomien alkioiden määrä. Yhteensä vertailuja on 15 – riippumatta siitä, onko joukko aluksi lajiteltu vai ei.

Tämä voidaan laskea myös seuraavasti:

Kuusi elementtiä kertaa viisi askelta; jaettuna kahdella, koska kaikkien askelten keskiarvona puolet elementeistä on vielä lajittelemattomia:

6 × 5 × ½ = 30 × ½ = 15

Jos korvataan 6 n:llä, saadaan

n × (n – 1) × ½

Kerronnassa saadaan:

½ n² – ½ n

Tässä termissä n:n suurin potenssi on n². Pienimmän alkion etsimisen aikakompleksisuus on siis O(n²) – sitä kutsutaan myös ”kvadraattiseksi ajaksi”.

Katsotaan nyt alkioiden vaihtamista. Jokaisessa vaiheessa (paitsi viimeisessä) vaihdetaan joko yksi alkio tai ei yhtään, riippuen siitä, onko pienin alkio jo oikeassa paikassa vai ei. Siten meillä on yhteensä korkeintaan n-1 vaihto-operaatiota, eli aikakompleksisuus on O(n) – jota kutsutaan myös ”lineaariseksi ajaksi”.

Kokonaiskompleksisuuden kannalta vain suurimmalla kompleksisuusluokalla on merkitystä, joten:

Valintalajittelun keskimääräisen, parhaan ja huonoimman tapauksen aikakompleksisuus on: O(n²)

* Termit ”aikakompleksisuus” ja ”O-notaatio” selitetään tässä artikkelissa esimerkkien ja kaavioiden avulla.

Javan Selection Sort -esimerkin suoritusaika

Teoriaa riittää! Olen kirjoittanut testiohjelman, joka mittaa Selection Sortin (ja kaikkien muiden tässä sarjassa käsiteltyjen lajittelualgoritmien) suoritusaikaa seuraavasti:

• Lajiteltavien elementtien määrä kaksinkertaistuu jokaisen iteraation jälkeen alun perin 1 024 elementistä 536 870 912 (= 229) elementtiin. Kaksi kertaa näin suurta joukkoa ei voida luoda Javassa.
• Jos testi kestää yli 20 sekuntia, joukkoa ei laajenneta enempää.
• Kaikki testit ajetaan lajittelemattomilla sekä nousevilla ja laskevilla esilajitelluilla elementeillä.
• Sallimme HotSpot-kääntäjän optimoida koodia kahdella lämmittelykierroksella. Tämän jälkeen testit toistetaan, kunnes prosessi keskeytetään.

Kunkin iteraation jälkeen ohjelma tulostaa kaikkien edellisten mittaustulosten mediaanin.

Tässä on Selection Sortin tulos 50 iteraation jälkeen (selkeyden vuoksi tämä on vain ote; täydellinen tulos löytyy täältä):

n	lajittelematon	nouseva	laskeva	laskeva
…	…	…	…
16.384	27,9 ms	26,8 ms	65,6 ms
32.768	108,0 ms	105,4 ms	265,4 ms
65.536	434,0 ms	424,3 ms	1.052,2 ms
131.072	1.729,8 ms	1.714,1 ms	4.209,9 ms
262.144	6.913,4 ms	6.880,2 ms	16.863,7 ms
524.288	27.649,8 ms	27.568,7 ms	67.537,8 ms

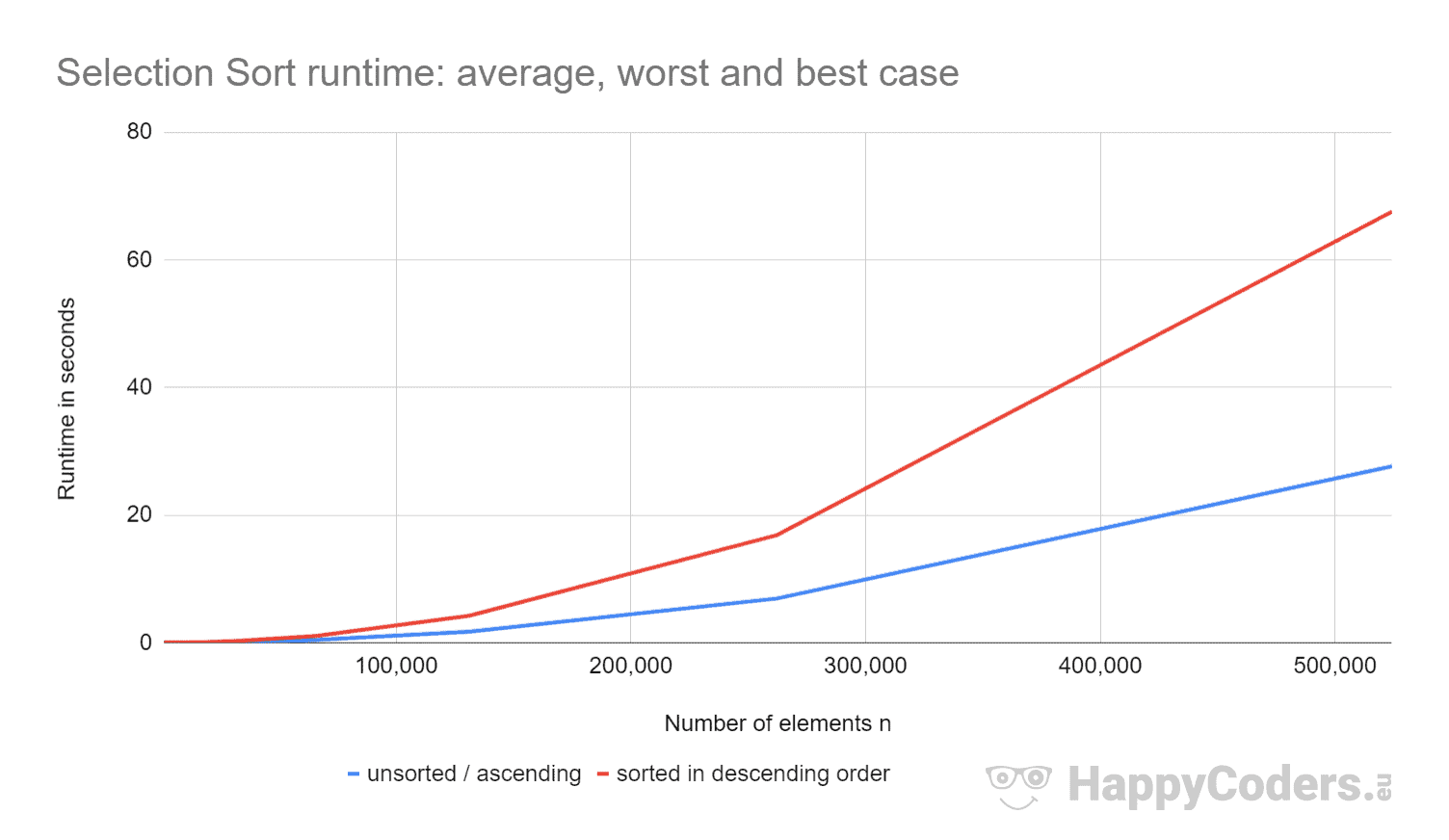
Tässä mittaukset vielä kerran kaaviona (jolloin olen näyttänyt ”lajittelemattomat” ja ”nousevat” yhtenä käyränä lähes identtisten arvojen vuoksi):

Hyvä huomata, että

• jos elementtien määrä kaksinkertaistuu, ajoaika noin nelinkertaistuu – riippumatta siitä, ovatko elementit etukäteen lajiteltuja vai eivät. Tämä vastaa odotettua aikakompleksisuutta O(n²).
• että nousevien lajiteltujen elementtien suoritusaika on hieman parempi kuin lajittelemattomien elementtien. Tämä johtuu siitä, että vaihto-operaatiot, joilla – kuten edellä analysoitiin – ei ole suurta merkitystä, eivät ole tässä tapauksessa tarpeellisia.
• että laskevien lajiteltujen alkioiden ajoaika on huomattavasti huonompi kuin lajittelemattomien alkioiden.

Miksi tämä johtuu?

Pahimman tapauksen ajoajan analyysi

Teoreettisesti pienimmän alkion etsimisen pitäisi kestää aina yhtä paljon aikaa lähtötilanteesta riippumatta. Ja vaihto-operaatioita pitäisi olla vain hieman enemmän alenevaan järjestykseen lajitelluilla elementeillä (alenevaan järjestykseen lajitelluilla elementeillä jokainen elementti pitäisi vaihtaa; lajittelemattomilla elementeillä melkein jokainen elementti pitäisi vaihtaa).

Käyttämällä CountOperations-ohjelmaa GitHub-tietovarastostani voimme nähdä eri operaatioiden määrän. Tässä ovat tulokset lajittelemattomille elementeille ja alenevaan järjestykseen lajitelluille elementeille, tiivistettynä yhteen taulukkoon:

.

n	Vertailu	Vaihdot lajittelemattomat	Vaihdot laskevassa järjestyksessä	minPos/min lajittelematon	minPos/min laskeva
…	…	…	…	…	…
512	130.816	504	256	2.866	66.047
1.024	523.776	1.017	512	6.439	263.167
2.048	2.096.128	2.042	1.024	14.727	1.050.623
4.096	8.386.560	4.084	2.048	30.758	4.198.399
8.192	33.550.336	8.181	4.096	69.378	16.785.407

Mittausarvoista voidaan nähdä:

• Alenevaan järjestykseen lajitelluilla alkioilla meillä on – odotetusti – yhtä paljon vertailuoperaatioita kuin lajittelemattomilla alkioilla – eli n × (n-1) / 2.
• Lajittelemattomilla elementeillä meillä on – kuten oletetaan – lähes yhtä monta vaihto-operaatiota kuin elementeillä: esimerkiksi 4096 lajittelemattomalla elementillä on 4084 vaihto-operaatiota. Nämä luvut vaihtelevat satunnaisesti testistä toiseen.
• Mutta alenevaan järjestykseen lajitelluilla elementeillä meillä on vain puolet vähemmän swap-operaatioita kuin elementtejä! Tämä johtuu siitä, että swapatessamme emme laita vain pienintä elementtiä oikeaan paikkaan, vaan myös vastaavaa swap-kumppania.

Kahdeksalla elementillä meillä on esimerkiksi neljä swap-operaatiota. Neljässä ensimmäisessä iteraatiossa meillä on kullakin yksi ja iteraatioissa viidestä kahdeksaan ei yhtään (siitä huolimatta algoritmi jatkaa suoritusta loppuun asti):

Mittauksista voimme lisäksi lukea:

• Syy siihen, miksi Selection Sort on niin paljon hitaampi, kun elementit on lajiteltu alenevaan järjestykseen, löytyy paikallisen muuttujan osoitusten määrästä (minPos ja min), kun etsitään pienintä elementtiä. Kun 8192 lajittelemattomalla elementillä näitä osoituksia on 69378, alenevaan järjestykseen lajitelluilla elementeillä tällaisia osoituksia on 16785407 eli 242 kertaa enemmän!

Miksi tämä valtava ero?

Analyysi pienimmän elementin etsimisen suoritusajasta

Alenevaan järjestykseen lajitelluilla elementeillä suuruusluokitus voidaan johtaa juuri yllä olevasta kuvasta. Pienimmän elementin etsintä rajoittuu oranssin ja oranssinsinisen laatikon kolmioon. Ylemmässä oranssissa osassa kunkin laatikon luvut pienenevät; oikeassa oranssin sinisessä osassa luvut taas kasvavat.

Kussakin oranssissa laatikossa ja oranssinsin sinisen laatikon ensimmäisessä osassa suoritetaan osoitusoperaatioita. Määritysoperaatioiden määrä minPos ja min kohdalla on siis kuvainnollisesti sanottuna noin ”neljäsosa neliöstä” – matemaattisesti ja täsmällisesti se on ¼ n² + n – 1.

Lajittelemattomien alkuaineiden kohdalla meidän täytyisi tunkeutua paljon syvemmälle asiaan. Se ei vain ylittäisi tämän artikkelin, vaan koko blogin laajuuden.

Sentähden rajoitan analyysini pieneen demo-ohjelmaan, joka mittaa, kuinka monta minPos/min-toimitusta on, kun etsitään pienintä elementtiä lajittelemattomasta joukosta. Tässä ovat keskiarvot 100 iteraation jälkeen (pieni ote; täydelliset tulokset löytyvät täältä):

n	keskimääräinen määrä minPos/min-toimituksia
1.024	7.08
4.096	8.61
16.385	8.94
65.536	11.81
262.144	12.22
1.048.576	14.26
4.194.304	14.71
16.777.216	16.44
67.108.864	17.92
268.435.456	20.27

Tässä kaaviossa logaritmisella x-akselilla:

Kaavio osoittaa erittäin kauniisti, että meillä on logaritminen kasvu, ts, jokaisella elementtien määrän kaksinkertaistumisella toimeksiantojen määrä kasvaa vain vakioarvon verran. Kuten sanoin, en aio mennä syvemmälle matemaattisiin taustoihin.

Tästä syystä näillä minPos/min-toimeksiannoilla ei ole juurikaan merkitystä lajittelemattomissa matriiseissa.

Valintalajittelun muut ominaisuudet

Seuraavissa osioissa käsittelen valintalajittelun tilakompleksisuutta, stabiilisuutta ja rinnakkaistettavuutta.

Valintalajittelun tilakompleksisuus

Valintalajittelun tilakompleksisuus on vakio, koska emme tarvitse lisämuistitilaa silmukkamuuttujien i ja j sekä apumuuttujien length, minPos ja min lisäksi.

Tämä tarkoittaa, että riippumatta siitä, kuinka monta elementtiä lajittelemme – kymmenen tai kymmenen miljoonaa – tarvitsemme aina vain näitä viittä lisämuuttujaa. Toteamme vakioajan olevan O(1).

Valintalajittelun stabiilius

Valintalajittelu vaikuttaa ensi silmäyksellä vakaalta: Jos lajittelematon osa sisältää useita elementtejä, joilla on sama avain, ensimmäiset pitäisi liittää lajiteltuun osaan ensin.

Mutta ulkonäkö pettää. Koska vaihtamalla kaksi elementtiä algoritmin toisessa alivaiheessa voi käydä niin, että lajittelemattoman osan tietyillä elementeillä ei ole enää alkuperäistä järjestystä. Tämä puolestaan johtaa siihen, että ne eivät enää esiinny alkuperäisessä järjestyksessä lajitellussa osassa.

Esimerkki voidaan rakentaa hyvin yksinkertaisesti. Oletetaan, että meillä on kaksi erilaista elementtiä, joilla on avain 2, ja yksi elementti, jolla on avain 1, jotka on järjestetty seuraavasti, ja lajitellaan ne Selection Sort -lajittelulla:

Ensimmäisessä vaiheessa ensimmäinen ja viimeinen elementti vaihdetaan. Näin elementti ”KAKSI” päätyy elementin ”kaksi” taakse – molempien elementtien järjestys on vaihdettu.

Toisessa vaiheessa algoritmi vertaa kahta takimmaista elementtiä. Molemmilla on sama avain, 2. Näin ollen yhtään elementtiä ei vaihdeta.

Kolmannessa vaiheessa jäljelle jää vain yksi elementti; tämä katsotaan automaattisesti lajitelluksi.

Kaksi elementtiä, joilla on avain 2, on siis vaihdettu alkuperäiseen järjestykseensä – algoritmi on epävakaa.

Stable Variant of Selection Sort

Valintalajittelusta voidaan tehdä stabiili siten, että pienintä alkua ei vaihdeta ensimmäiseen alkioon vaiheessa kaksi, vaan kaikki alkion ja pienimmän alkion välissä olevat alkion osat siirretään yhden paikan verran oikealle ja pienin alkio lisätään alkuun.

Vaikka aikakompleksisuus säilyy tämän muutoksen ansiosta samana, ylimääräiset siirtymiset johtavat huomattavaan suorituskyvyn heikkenemiseen ainakin silloin, kun lajitellaan joukkoa.

Linkitetyllä listalla lajiteltavan elementin leikkaaminen ja liittäminen voitaisiin tehdä ilman merkittävää suorituskyvyn heikkenemistä.

Valintalajittelun rinnakkaistettavuus

Emmekä voi rinnakkaistaa ulompaa silmukkaa, koska se vaihtaa matriisin sisältöä jokaisessa iteraatiossa.

Sisempi silmukka (pienimmän alkion etsiminen) voidaan rinnakkaistaa jakamalla array, etsimällä rinnakkain pienin alkio jokaisesta osamassasta ja yhdistämällä välitulokset.

Selection Sort vs. Insertion Sort

Kumpi algoritmi on nopeampi, Selection Sort vai Insertion Sort?

Vertaillaan mittaustuloksiani Java-toteutuksissani.

Jättän parhaan mahdollisen tapauksen pois. Insertion Sortilla parhaan tapauksen aikakompleksisuus on O(n) ja kesti alle millisekunnin 524 288 elementtiin asti. Parhaassa tapauksessa Insertion Sort on siis millä tahansa alkioiden määrällä kertaluokkaa nopeampi kuin Selection Sort.

n	Valintalajittelu lajittelematon	Sisällyslajittelu lajittelematon	Valintalajittelu laskeva	Sisällyslajittelu laskeva
…	…	…	…	…
16.384	27,9 ms	21,9 ms	65,6 ms	43,6 ms
32.768	108,0 ms	87,9 ms	265,4 ms	175,8 ms
65.536	434,0 ms	350,4 ms	1.052,2 ms	697,6 ms
131.072	1.729,8 ms	1.398,9 ms	4.209,9 ms	2.840,0 ms
262.144	6.913,4 ms	5.706,8 ms	16.863,7 ms	11.517,4 ms
524.288	27.649,8 ms	23.009,7 ms	67.537,8 ms	46.309,3 ms

Ja vielä kerran kaaviona:

Insertion Sort on siis nopeampi kuin Selection Sort paitsi parhaassa tapauksessa myös keskimääräisessä ja huonoimmassa tapauksessa.

Syy tähän on se, että Insertion Sort vaatii keskimäärin puolet vähemmän vertailuja. Muistutuksena mainittakoon, että Insertion Sortilla meillä on vertailuja ja siirtoja keskimäärin jopa puolet lajitelluista elementeistä; Selection Sortilla joudumme etsimään pienimmän elementin kaikista lajittelemattomista elementeistä jokaisessa vaiheessa.

Selection Sortilla on huomattavasti vähemmän kirjoitusoperaatioita, joten Selection Sort voi olla nopeampi silloin, kun kirjoitusoperaatiot ovat kalliita. Tämä ei päde matriiseihin tehtäviin peräkkäisiin kirjoituksiin, sillä ne tehdään useimmiten suorittimen välimuistiin.

Käytännössä Selection Sortia ei siis käytetä juuri koskaan.

Yhteenveto

Selection Sort on helposti implementoitava ja tyypillisessä toteutuksessaan epästabiili lajittelualgoritmi, jonka keskimääräisen, parhaan ja huonoimman tapauksen aikakompleksisuuden keskiarvo on O(n²).

Selection Sort on hitaampi kuin Insertion Sort, minkä vuoksi sitä käytetään harvoin käytännössä.

Tästä yleiskatsauksesta kaikkiin lajittelualgoritmeihin ja niiden ominaisuuksiin löydät lisää lajittelualgoritmeja artikkelisarjan ensimmäisestä osasta.

Jos pidit artikkelista, jaa sitä rohkeasti jollakin lopussa olevista jakopainikkeista. Haluatko saada ilmoituksen sähköpostitse, kun julkaisen uuden artikkelin? Tilaa sitten uutiskirjeeni seuraavalla lomakkeella.