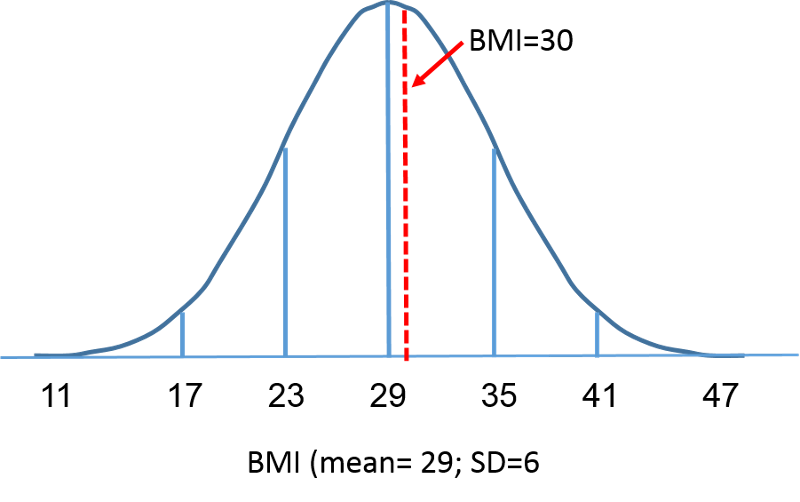
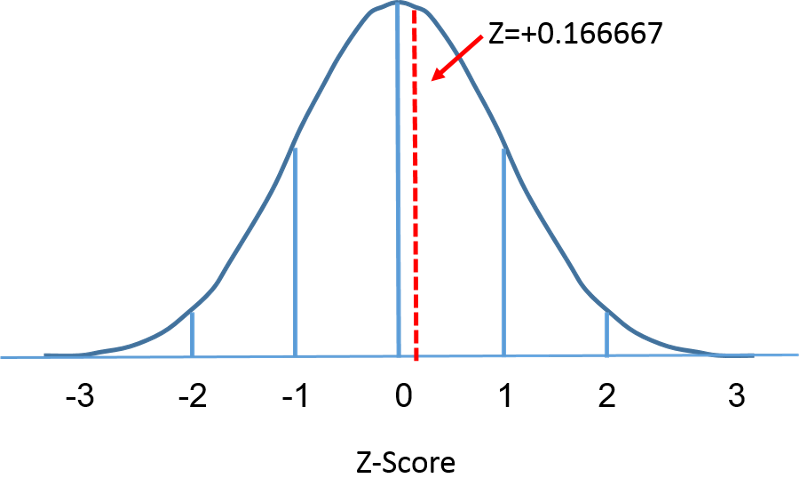
Normaalijakauma on normaalijakauma, jonka keskiarvo on nolla ja keskihajonta 1. Normaalijakauman keskipiste on nollassa, ja keskihajonnan avulla saadaan selville, kuinka paljon tietty mittaus poikkeaa keskiarvosta. Standardinormaalijakauman osalta 68 % havainnoista on yhden keskihajonnan sisällä, 95 % on kahden keskihajonnan sisällä ja 99,9 % on kolmen keskihajonnan sisällä. Tähän asti olemme käyttäneet ”X:ää” kuvaamaan kiinnostavaa muuttujaa (esim. X=BMI, X=pituus, X=paino). Kun käytämme vakionormaalijakaumaa, käytämme kuitenkin sanaa ”Z” viittaamaan muuttujaan vakionormaalijakauman yhteydessä. Normalisoinnin jälkeen edellisellä sivulla käsitelty BMI=30 näkyy alla, kun se makaa 0,16667 yksikköä oikealla olevan vakionormaalijakauman keskiarvon 0 yläpuolella.
 ====
====
Koska vakiokäyrän alapuolinen pinta-ala on = 1, voimme ryhtyä määrittelemään tarkemmin tietyn havainnon todennäköisyyksiä. Minkä tahansa Z-pistemäärän osalta voimme laskea kyseisen Z-pistemäärän vasemmalla puolella olevan käyrän alle jäävän pinta-alan. Alla olevassa kehyksessä olevassa taulukossa esitetään todennäköisyydet standardinormaalijakaumalle. Tutki taulukkoa ja huomaa, että Z-pistemäärän 0,0 todennäköisyys on 0,50 eli 50 % ja Z-pistemäärän 1 eli yhden keskihajonnan keskiarvon yläpuolella todennäköisyys on 0,8413 eli 84 %. Tämä johtuu siitä, että yksi keskihajonta keskiarvon ylä- ja alapuolella kattaa noin 68 % alueesta, joten yksi keskihajonta keskiarvon yläpuolella edustaa puolta tästä 34 %:sta. Eli 50 % keskiarvon alapuolella plus 34 % keskiarvon yläpuolella antaa meille 84 %.
Normaalijakauman Z todennäköisyydet
![]()
Tämä taulukko on järjestetty siten, että siinä ilmoitetaan käyrän alapuolella oleva pinta-ala, joka on vasemmanpuoleinen tai pienempi kuin tietty arvo eli ”Z-arvo”. Tässä tapauksessa, koska keskiarvo on nolla ja keskihajonta on 1, Z-arvo on keskihajonnan yksiköiden määrä keskiarvosta, ja pinta-ala on todennäköisyys havaita arvoa, joka on pienempi kuin kyseinen Z-arvo. Huomaa myös, että taulukossa näytetään todennäköisyydet Z:n kahden desimaalin tarkkuudella. Yksikköpaikka ja ensimmäinen desimaali näkyvät vasemmassa sarakkeessa, ja toinen desimaali näkyy ylärivin poikki.
Mutta palataanpa takaisin kysymykseen todennäköisyydestä, että BMI on alle 30, eli P(X<30). Voimme vastata tähän kysymykseen käyttämällä tavallista normaalijakaumaa. Alla olevissa kuvissa on esitetty 60-vuotiaiden miesten BMI:n jakaumat ja vakionormaalijakauma vierekkäin.
Kehon painoindeksin jakauma ja vakionormaalijakauma
 ====
====
Kummankin käyrän alle jäävä pinta-ala on yksi, mutta X-akselin skaalaus on erilainen. Huomaa kuitenkin, että katkoviivan vasemmalla puolella olevat alueet ovat samat. BMI-jakauma vaihtelee välillä 11-47, kun taas standardoitu normaalijakauma, Z, vaihtelee välillä -3-3. Haluamme laskea P(X < 30). Tätä varten voimme määrittää Z-arvon, joka vastaa arvoa X = 30, ja käyttää sitten edellä olevaa vakioidun normaalijakauman taulukkoa todennäköisyyden tai käyrän alle jäävän alueen löytämiseksi. Seuraava kaava muuntaa X-arvon Z-arvoksi, jota kutsutaan myös standardoiduksi arvoksi:

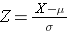
jossa μ on muuttujan X keskiarvo ja σ on muuttujan X keskihajonta.
Laskettaaksemme P(X < 30) muunnamme X=30 vastaavaksi Z-pistemääräksi (tätä kutsutaan standardoinniksi):

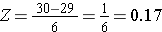
Siten P(X < 30) = P(Z < 0.17). Voimme sitten etsiä tätä Z-pistemäärää vastaavan todennäköisyyden tavallisesta normaalijakaumataulukosta, joka osoittaa, että P(X < 30) = P(Z < 0,17) = 0,5675. Näin ollen todennäköisyys sille, että 60-vuotiaalla miehellä on BMI alle 30, on 56,75 %.
Muutama esimerkki
Käyttäen samaa BMI:n jakaumaa, mikä on todennäköisyys sille, että 60-vuotiaalla miehellä on BMI yli 35? Toisin sanoen, mikä on P(X > 35)? Jälleen normalisoimme:

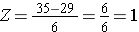
Mennään nyt normaalijakauman standarditaulukkoon etsimään P(Z>1) ja Z=1.00:lle löydämme, että P(Z<1.00) = 0.8413. Huomaa kuitenkin, että taulukko antaa aina todennäköisyyden, että Z on pienempi kuin annettu arvo, eli se antaa meille P(Z<1)=0,8413.
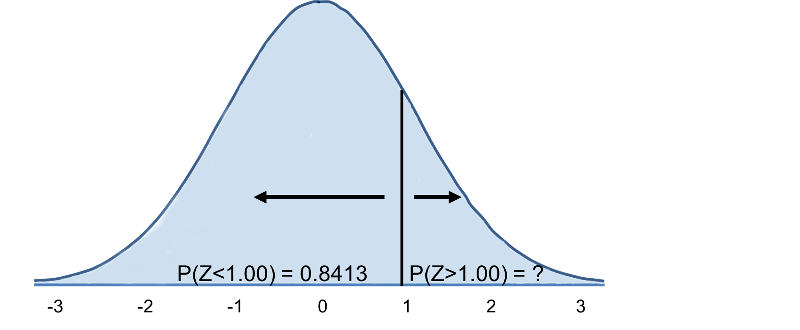
Siten P(Z>1)=1-0,8413=0,1587. Tulkinta: Lähes 16 %:lla 60-vuotiaista miehistä on BMI yli 35.
Normaalitodennäköisyyslaskuri
![]()
![]()
Z-pisteet R:llä
Vaihtoehtona normaalitodennäköisyyksien etsimiseen taulukosta tai Excelin käyttämiseen voimme käyttää R:ää todennäköisyyksien laskemiseen. Esimerkiksi
> pnorm(0)
Z-pistemäärällä 0 (minkä tahansa jakauman keskiarvo) on 50 % alueesta vasemmalla. Mikä on todennäköisyys sille, että yllä olevaan perusjoukkoon kuuluvan 60-vuotiaan miehen BMI on alle 29 (keskiarvo)? Z-pistemäärä olisi 0 ja pnorm(0)=0,5 eli 50 %.
Millä todennäköisyydellä 60-vuotiaalla miehellä on BMI alle 30? Z-pistemäärä oli 0,16667.
> pnorm(0,16667)
Todennäköisyys on siis 56,6 %.
Millä todennäköisyydellä 60-vuotiaalla miehellä on BMI yli 35?
35-29=6, joka on yhden keskihajonnan keskiarvon yläpuolella. Voimme siis laskea alueen vasemmalle
> pnorm(1)
ja sitten vähentää tuloksen arvosta 1,0.
1-0,8413447= 0,1586553
Siten todennäköisyys sille, että 60-vuotiaan miehen BMI on yli 35, on 15,8 %.
Vai voimmeko käyttää R:ää koko asian laskemiseen yhdessä vaiheessa seuraavasti:
> 1-pnorm(1)
Todennäköisyys arvoalueelle

Millä todennäköisyydellä 60-vuotiaalla miehellä on BMI välillä 30-35? Huomaa, että tämä on sama kuin kysyä, kuinka suurella osalla 60-vuotiaista miehistä BMI on välillä 30-35. Tarkemmin sanottuna haluamme P(30 < X < 35)? Laskimme aiemmin P(30<X) ja P(X<35); miten näitä kahta tulosta voidaan käyttää sen todennäköisyyden laskemiseen, että BMI on välillä 30 ja 35? Yritä muotoilla ja vastata itse ennen kuin katsot alla olevaa selitystä.
Vastaus