Mitkä ovat nuottien taajuudet?

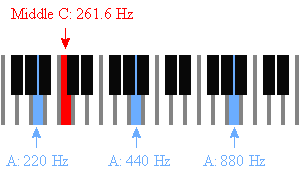
Alla olevasta taajuustaulukosta löydät A = 440 Hz, ja sitten

A# = 466,16 Hz,
B = 493,88 Hz,
C = 523,25 Hz, jne.

Myös keskimmäinen C: 261.63 Hz.

Nämä löydetään käyttämällä

taajuutta `= 440×2^(n”/”12)`

for `n = -21, -19, …, 27`

Missä tämä kaava on peräisin?

Tämä ongelma toi mieleeni Korkokomponentin, jonka tapasimme aiemmin Money Mathissa. Taajuuden on kaksinkertaistuttava joka `12` nuotin välein (koska jokaisessa oktaavissa on `7` valkoisia nuotteja ja `5` mustia nuotteja.)

Tässä on kuvaaja tästä suhteesta:

taajuus `= 440×2^(n”/”12)`

Tämä on eksponentiaalinen käyrästö, johon törmäsimme aiemmin Eksponentiaalisten funktioiden kuvaajissa.

Equal Tempered Tuning

Mielenkiintoinen ongelma on kohdannut soitinrakentajia satojen vuosien ajan. Saadaksemme ”täydellisen 5. sävelen” (vaikkapa A:n ja sen yläpuolella olevan E:n väli), meidän on soitettava sävel, jonka taajuus on `1,5` kertaa A:n taajuus.

Viululla (tai alttoviululla tai millä tahansa kitkattomalla jousisoittimella) tämä on mahdollista, ja voimme soittaa kauniin, täydellisen E:n, jonka taajuus on `440 × 1,5 = 660\”Hz”`. Huomatkaa kuitenkin (yllä olevasta taajuustaulukosta), että piano, joka soittaa saman sävelen, soittaa E `= 659.26\”Hz”` .

Noin 400 vuotta sitten koskettimet (tavallisesti cembalot ja urut) viritettiin tietylle näppäinryhmälle, jotta kaikki soittimet, erityisesti jouset, kuulostaisivat ”oikeilta” näissä näppäimissä. Cembalo kuulosti loistavalta näissä äänensävyissä, mutta melko kamalalta muissa, toisiinsa liittymättömissä äänensävyissä (vaikkapa B:ssä).

Bachin aikana oli itse asiassa käytössä useita erilaisia viritysjärjestelmiä, kuten meantone (joka pyrki saamaan duurin 3:t kuulostamaan hyvältä, mutta ei ollut yhtä huolissaan duurin 5:nnen äänenlaadusta, mikä johti siihen, että jotkin koskettimet eivät olleet käyttökelpoisia) ja Werckmeisterin viritys vuodelta 1691, joka mahdollisti säveltäjille musiikin luomisen missä tahansa koskettimessa (mikä johti siihen, että eri koskettimilla oli erilainen soinnillinen laatu).

1900-luvun alussa päätettiin virittää koskettimet niin, että nuotit olivat tasaisin välein (kuten edellä esitetyssä taulukossa esitetyt taajuudet). Tätä kutsutaan tasavireiseksi viritykseksi. Tällainen viritys tunnettiin jo Bachin aikana, mutta se hylättiin, koska sitä pidettiin liian ”mauttomana” (kaikilla koskettimilla on sama äänenlaatu) ja koska ei ollut olemassa taajuusmittauslaitteita, jotka olisivat mahdollistaneet tarkan virityksen.

Epäonnekseen tasatahtinen viritys tarkoittaa, että kaikkien jousisoittimien kohdalla on otettava huomioon soittimien väliset vähäiset virityserot, kun mukana ovat myös koskettimet. Tästä syystä jouset ovat yleensä tyytyväisimpiä soitettaessa vain muiden jousien kanssa.