Biografia
Johannes Kepler muistetaan nykyään lähinnä siitä, että hän löysi kolme hänen nimeään kantavaa planeettojen liikkeen lakia, jotka julkaistiin vuosina 1609 ja 1619). Hän teki myös merkittävää työtä optiikan alalla (1604, 1611), löysi kaksi uutta säännönmukaista moniulotteista moniulottuvuutta (1619), käsitteli ensimmäistä kertaa matemaattisesti yhtäläisten pallojen tiivistä pakkautumista (mikä johti selitykseen hunajakennon solujen muodosta, 1611), antoi ensimmäisen todistuksen logaritmien toiminnasta (1624) ja kehitti menetelmän kiertokappaleiden tilavuuksien selvittämiseksi, jonka voidaan (jälkikäteen ajateltuna!) katsoa myötävaikuttaneen myös laskutoimitusten kehittelyn kehitystyön edistämiseen (1615, 1616). Lisäksi hän laski tarkimmat tähän mennessä tunnetut tähtitieteelliset taulukot, joiden jatkuva tarkkuus auttoi paljon heliosentrisen tähtitieteen totuuden vakiinnuttamisessa (Rudolfin taulukot, Ulm, 1627).
Keplerin kirjeenvaihdosta on säilynyt suuri määrä. Monet hänen kirjeistään vastaavat lähes tieteellistä artikkelia (tieteellisiä lehtiä ei vielä ollut), ja kirjeenvaihtajat näyttävät säilyttäneen niitä, koska ne olivat kiinnostavia. Näin ollen tiedämme melko paljon Keplerin elämästä ja jopa hänen luonteestaan. Osittain tästä syystä Kepler on tehnyt jonkinlaisen uran enemmän tai vähemmän fiktiivisenä hahmona (ks. historiografinen huomautus jäljempänä).
Lapsuus
Kepler syntyi Weil der Stadtin pikkukaupungissa Schwabissa ja muutti vanhempiensa kanssa läheiseen Leonbergiin vuonna 1576. Hänen isänsä oli palkkasotilas ja äitinsä majatalon pitäjän tytär. Johannes oli heidän ensimmäinen lapsensa. Hänen isänsä lähti kotoa viimeisen kerran, kun Johannes oli viisivuotias, ja hänen uskotaan kuolleen sodassa Alankomaissa. Lapsena Kepler asui äitinsä kanssa isoisänsä majatalossa. Hän kertoo, että hänellä oli tapana auttaa tarjoilemalla majatalossa. Voi kuvitella, että asiakkaat olivat joskus hämmentyneitä lapsen epätavallisesta laskutaidosta.
Keplerin varhaiskasvatus tapahtui paikallisessa koulussa ja sen jälkeen läheisessä pappisseminaarissa, josta hän aikoi tulla pappisvihkimykseksi ja kirjoittautui Tübingenin yliopistoon, joka oli tuolloin (kuten nykyäänkin) luterilaisen ortodoksisuuden linnakkeena.
Keplerin mielipiteet
Kepler oli koko ikänsä syvästi uskonnollinen mies. Kaikissa hänen kirjoituksissaan on lukuisia viittauksia Jumalaan, ja hän näki työnsä täyttävän kristillisen velvollisuutensa ymmärtää Jumalan tekoja. Koska ihminen, kuten Kepler uskoi, oli luotu Jumalan kuvaksi, hän kykeni selvästi ymmärtämään Jumalan luomaa maailmankaikkeutta. Lisäksi Kepler oli vakuuttunut siitä, että Jumala oli luonut maailmankaikkeuden matemaattisen suunnitelman mukaisesti (uskomus, joka esiintyy Platonin teoksissa ja liittyy Pythagoraan). Koska tuohon aikaan yleisesti hyväksyttiin, että matematiikka tarjosi varman menetelmän, jolla voitiin päätyä maailmaa koskeviin totuuksiin (Eukleideen yleisiä käsitteitä ja postulaatteja pidettiin todellisuudessa totena), meillä oli tässä strategia maailmankaikkeuden ymmärtämiseksi. Koska jotkut kirjoittajat ovat nimittäneet Kepleriä irrationaaliseksi, on syytä huomata, että tämä varsin toiveikas epistemologia on todellakin hyvin kaukana mystikon vakaumuksesta, jonka mukaan asioita voidaan ymmärtää vain epätäsmällisellä tavalla, joka nojaa järjen ulottumattomissa oleviin oivalluksiin. Kepler kiittelee tosiaan toistuvasti Jumalaa siitä, että hän on antanut hänelle oivalluksia, mutta nämä oivallukset esitetään rationaalisina.
Yliopistokoulutus
Tihen aikaan oli tavallista, että kaikki yliopisto-opiskelijat osallistuivat ”matematiikan” kursseille. Periaatteessa tähän kuuluivat neljä matemaattista tiedettä: aritmetiikka, geometria, tähtitiede ja musiikki. Näyttää kuitenkin siltä, että se, mitä opetettiin, riippui kyseisestä yliopistosta. Tübingenissä Kepleriä opetti tähtitiedettä yksi sen ajan johtavista tähtitieteilijöistä, Michael Mästlin (1550-1631). Opetussuunnitelman mukainen tähtitiede oli tietenkin geosentrinen tähtitiede eli Ptolemaioksen järjestelmän nykyversio, jossa kaikki seitsemän planeettaa – Kuu, Merkurius, Venus, Aurinko, Mars, Jupiter ja Saturnus – liikkuivat maapallon ympäri, ja niiden sijainnit kiintotähtiin nähden laskettiin yhdistämällä kiertoliikkeet. Tämä järjestelmä oli enemmän tai vähemmän sopusoinnussa nykyisten (aristoteelisten) fysiikkakäsitysten kanssa, vaikka siinä olikin tiettyjä vaikeuksia, kuten se, voitiinko pitää ”yhtenäisenä” (ja siten hyväksyttävänä ilmeisen ikuisena) kiertoliikettä, joka ei ollut yhtenäinen oman keskipisteensä ympärillä vaan jonkin toisen pisteen ympärillä (jota kutsuttiin ”ekvantiksi”). Näyttää kuitenkin siltä, että kaiken kaikkiaan tähtitieteilijät (jotka pitivät itseään ”matemaatikkoina”) tyytyivät laskemaan planeettojen sijainteja ja jättivät luonnonfilosofien huoleksi sen, vastasivatko matemaattiset mallit fysikaalisia mekanismeja. Kepler ei omaksunut tätä asennetta. Hänen varhaisimmassa julkaistussa teoksessaan (1596) ehdotetaan, että tarkastellaan planeettojen todellisia ratoja, ei niiden rakentamiseen käytettyjä ympyröitä.
Tübingenissä Kepler opiskeli matematiikan lisäksi myös kreikkaa ja hepreaa (molempia tarvittiin pyhien kirjoitusten lukemiseen niiden alkuperäisillä kielillä). Opetus tapahtui latinaksi. Ensimmäisen vuoden lopussa Kepler sai kiitettäviä kaikesta muusta paitsi matematiikasta. Todennäköisesti Mästlin yritti kertoa hänelle, että hän pystyi parempaankin, sillä Kepler oli itse asiassa yksi niistä valituista oppilaista, joille hän päätti opettaa edistyneempää tähtitiedettä tutustuttamalla heidät Kopernikuksen uuteen, heliosentriseen kosmologiseen järjestelmään. Mästliniltä Kepler sai tietää, että Kiertokulkuja käsittelevän kirjan esipuhe, jossa selitetään, että kyseessä oli ”pelkkää matematiikkaa”, ei ollut Kopernikuksen kirjoittama. Kepler näyttää hyväksyneen lähes välittömästi, että kopernikaaninen järjestelmä oli fysikaalisesti totta; hänen syitään sen hyväksymiseen käsitellään hänen ensimmäisen kosmologisen mallinsa yhteydessä (ks. jäljempänä).
Näyttää siltä, että jo Keplerin opiskeluaikana oli viitteitä siitä, että hänen uskonnolliset vakaumuksensa eivät olleet täysin sopusoinnussa Tübingenissä vallitsevan ja Confessio Augustana Ⓣ -teoksessa muotoillun ortodoksisen luterilaisuuden kanssa. Keplerin ongelmat tämän protestanttisen ortodoksisuuden kanssa koskivat aineen ja ”hengen” (ei-materiaalisen olennon) oletettua suhdetta eukaristiaopissa. Tämä liittyy Keplerin tähtitieteeseen sikäli, että hänellä oli ilmeisesti jokseenkin samanlaisia älyllisiä vaikeuksia selittää, miten Auringosta peräisin oleva ”voima” voisi vaikuttaa planeettoihin. Kirjoituksissaan Keplerillä on tapana esittää mielipiteitään, mikä on historioitsijoiden kannalta erittäin kätevää. Todellisessa elämässä vaikuttaa todennäköiseltä, että samanlainen taipumus avoimuuteen sai Tübingenin viranomaiset epäilemään perustellusti Keplerin uskonnollista oikeaoppisuutta. Nämä saattavat selittää, miksi Mästlin suostutteli Keplerin luopumaan pappisvihkimyssuunnitelmista ja ryhtymään sen sijaan matematiikan opettajaksi Graziin. Uskonnollinen suvaitsemattomuus kärjistyi seuraavina vuosina. Kepler erotettiin kirkosta vuonna 1612. Tämä aiheutti hänelle paljon tuskaa, mutta huolimatta hänen (siihen mennessä) suhteellisen korkeasta yhteiskunnallisesta asemastaan keisarillisena matemaatikkona hän ei koskaan onnistunut saamaan kieltoa kumottua.
Keplerin ensimmäinen kosmologinen malli (1596)
Kopernikaanisessa järjestelmässä oli tavanomaisen geosentrisen tähtitieteen seitsemän planeetan sijasta vain kuusi planeettaa, ja Kuusta oli tullut astronomialle aiemmin tuntematon kappale, jota Kepler kutsui myöhemmin ”satelliitiksi” (nimitys, jonka hän keksi vuonna 1610 kuvaamaan kuita, jotka Galilei oli havainnut kiertävän Jupiteria, ja joka tarkoitti kirjaimellisesti ”saattajaa”). Miksi kuusi planeettaa?
Lisäksi geosentrisessä tähtitieteessä ei ollut mitään keinoa käyttää havaintoja planeettojen suhteellisten kokojen selvittämiseksi, vaan niiden oletettiin yksinkertaisesti olevan kosketuksissa toisiinsa. Tämä ei näyttänyt vaativan selitystä, koska se sopi hyvin luonnonfilosofien uskomukseen, jonka mukaan koko järjestelmä oli kääntynyt uloimman pallon liikkeestä, joka oli yksi (tai ehkä kaksi) ”kiinteiden” tähtien pallon (niiden, joiden kuvio muodosti tähdistöt) takana, Saturnuksen pallon takana. Kopernikaanisessa järjestelmässä se tosiasia, että kunkin planeetan liikkeen vuotuinen komponentti heijasti Maan vuotuista liikettä, mahdollisti sen, että havaintojen avulla voitiin laskea kunkin planeetan radan koko, ja kävi ilmi, että planeettojen välillä oli valtavia välejä. Miksi juuri nämä välit?
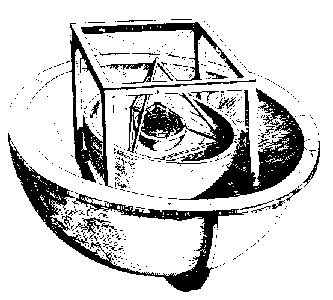
Keplerin vastaus näihin kysymyksiin, joka on kuvattu teoksessa Mysterium cosmographicum Ⓣ, Tübingen, 1596, näyttää 1900-luvun lukijasta oudolta (ks. kuva oikealla). Hän ehdotti, että jos piirretään pallo koskettamaan Saturnuksen radan sisäpuolta ja kuutio merkitään palloon, niin kuutioon merkitty pallo olisi Jupiterin rataa kiertävä pallo. Jos Jupiterin radan kuvaavaan palloon piirretään säännöllinen tetraedri, tetraedrin sisäkehä on Marsin radan kuvaava pallo, ja niin edelleen sisäänpäin, jolloin Marsin ja Maan väliin jää säännöllinen dodekaedri, Maan ja Venuksen väliin säännöllinen ikosaedri ja Venuksen ja Merkuriuksen väliin säännöllinen oktaedri. Tämä selittää planeettojen lukumäärän täydellisesti: kuperia säännöllisiä kiinteitä kappaleita on vain viisi (kuten todistetaan Eukleideen alkuaineiden kirjassa 13). Se sopii myös vakuuttavasti yhteen Kopernikuksen päättelemien ratojen koon kanssa, sillä suurin virhe on alle 10 prosenttia (mikä on kosmologiselta mallilta vielä nykyäänkin hämmästyttävän hyvä). Kepler ei ilmaissut itseään prosentuaalisten virheiden muodossa, ja hänen mallinsa on itse asiassa ensimmäinen matemaattinen kosmologinen malli, mutta on helppo ymmärtää, miksi hän uskoi, että havainnolliset todisteet tukevat hänen teoriaansa.
Kepler näki kosmologisen teoriansa tarjoavan todisteita kopernikaaniselle teorialle. Ennen oman teoriansa esittelyä hän esitti perusteluja, joilla hän halusi osoittaa itse kopernikaanisen teorian uskottavuuden. Kepler väittää, että sen edut geosentriseen teoriaan nähden ovat sen suuremmassa selitysvoimassa. Kopernikaaninen teoria voi esimerkiksi selittää, miksi Venus ja Merkurius eivät koskaan näy kovin kaukana Auringosta (ne sijaitsevat Maan ja Auringon välissä), kun taas geosentrisessä teoriassa tälle seikalle ei ole selitystä. Kepler luettelee yhdeksän tällaista kysymystä Mysterium cosmographicum Ⓣ -teoksen ensimmäisessä luvussa.
Kepler teki tämän teoksen opettaessaan Grazissa, mutta kirjan näki painosta läpi Tübingenissä Mästlin. Yhdenmukaisuus havainnoista johdettujen arvojen kanssa ei ollut tarkka, ja Kepler toivoi, että paremmat havainnot parantaisivat yhdenmukaisuutta, joten hän lähetti jäljennöksen Mysterium cosmographicumista yhdelle aikansa johtavista havaintotähtitieteilijöistä, Tycho Brahelle (1546 – 1601). Tycho, joka työskenteli tuolloin Prahassa (tuolloin Pyhän saksalais-roomalaisen keisarikunnan pääkaupungissa), oli itse asiassa jo kirjoittanut Mästlinille etsiessään matemaattista avustajaa. Kepler sai työn.
”Sota Marsin kanssa”
Tychon prioriteetit eivät luonnollisestikaan olleet samat kuin Keplerin, ja Kepler joutui pian työskentelemään Marsin radan vaikeasti ratkaistavan ongelman parissa. Hän jatkoi sen parissa työskentelyä sen jälkeen, kun Tycho kuoli (vuonna 1601) ja Kepler tuli hänen seuraajakseen keisarillisena matemaatikkona. Perinteisesti kiertoradat koostuivat ympyröistä, ja ympyröiden suhteellisten säteiden ja paikkojen määrittämiseen tarvittiin melko vähän havaintoarvoja. Tycho oli tehnyt valtavan määrän havaintoja, ja Kepler päätti hyödyntää niitä parhaalla mahdollisella tavalla. Hänellä oli käytössään niin paljon havaintoja, että kun hän oli laatinut mahdollisen radan, hän pystyi tarkistamaan sen suhteessa muihin havaintoihin, kunnes oli päästy tyydyttävään sopimukseen. Kepler päätteli, että Marsin rata oli ellipsi, jonka yhdessä polttopisteessä oli Aurinko (tulos, jota laajennettuna kaikkiin planeettoihin kutsutaan nykyään ”Keplerin ensimmäiseksi laiksi”), ja että planeetan ja Auringon yhdistävä viiva pyyhkäisi yhtä suuria alueita samassa ajassa, kun planeetta kuvasi rataansa (”Keplerin toinen laki”), eli pinta-alaa käytetään ajan mittana. Kun tämä työ oli julkaistu Astronomia nova -lehdessä, … Ⓣ, Heidelberg, 1609, Kepler löysi muiden planeettojen kiertoradat ja totesi näin, että nämä kaksi lakia pätevät myös niihin. Molemmat lait suhteuttavat planeetan liikkeen Aurinkoon; Keplerin kopernikaanismi oli ratkaisevassa asemassa hänen päättelyssään ja johtopäätöksissään.
Varsinainen Marsia koskeva laskentaprosessi oli suunnattoman työläs – aritmeettisia laskutoimituksia on säilynyt lähes tuhat folioarkkia – ja Kepler itse kutsuu tätä työtä ”sodakseni Marsin kanssa”, mutta tuloksena saatiin kiertorata, joka vastaa nykyaikaisia mittaustuloksia niin tarkkaan, että vertailussa on otettava huomioon kiertoradan sekulaariset muutokset, jotka ovat tapahtuneet sitten Keplerin ajan.
Havaintovirhe
Keplerin menetelmälle, jolla hän tarkisti mahdollisia ratoja havaintoja vastaan, oli ratkaisevan tärkeää, että hänellä oli käsitys siitä, mikä olisi hyväksyttävä riittäväksi vastaavuudeksi. Tästä seuraa havaintovirheen käsitteen ensimmäinen nimenomainen käyttö. Kepler saattoi olla tämän käsitteen velkaa ainakin osittain Tycholle, joka teki yksityiskohtaisia tarkistuksia instrumenttiensa suorituskyvystä (ks. Brahen elämäkerta).
Optiikka ja vuoden 1604 uusi tähti
Työ Marsista oli pääosin valmis vuoteen 1605 mennessä, mutta kirjan julkaiseminen viivästyi. Sillä välin vastauksena huoliin Kuun erilaisesta näennäisestä halkaisijasta suoraan ja camera obscuran avulla havainnoituna Kepler teki jonkin verran työtä optiikan parissa ja keksi ensimmäisen oikean matemaattisen teorian camera obscurasta ja ensimmäisen oikean selityksen ihmissilmän toiminnasta, jossa verkkokalvolle muodostuu ylösalaisin oleva kuva. Nämä tulokset julkaistiin teoksessa Ad Vitellionem paralipomena, quibus astronomiae pars optica traditur Ⓣ, Frankfurt, 1604. Hän kirjoitti myös vuoden 1604 uudesta tähdestä, jota nykyään kutsutaan tavallisesti ”Keplerin supernovaksi”, ja hylkäsi lukuisia selityksiä ja huomautti eräässä kohdassa, että tämä tähti saattoi tietysti olla vain erikoinen luomus, ”mutta ennen kuin tulemme siihen, meidän on mielestäni kokeiltava kaikkea muuta” De stella nova Ⓣ, Praha, 1606, luku 22, KGW 1, s. 257, rivi 23.
Sen jälkeen, kun Galilei oli käyttänyt kaukoputkea Jupiterin kuiden löytämiseen, joka julkaistiin Sidereal Messenger -teoksessa (Venetsia, 1610), johon Kepler oli kirjoittanut innostuneen vastauksen (1610), Kepler kirjoitti tutkimuksen linssien ominaisuuksista (ensimmäinen tällainen optiikkaa käsittelevä teos), jossa hän esitteli uudenlaisen kaukoputkimalliston, jossa käytettiin kahta kuperaa linssiä (Dioptrice, Praha, 1611). Tämä rakenne, jossa lopullinen kuva on käänteinen, oli niin menestyksekäs, että sitä ei nykyään yleensä kutsuta kepleriläiseksi kaukoputkeksi vaan yksinkertaisesti tähtitieteelliseksi kaukoputkeksi.
Lähdössä Prahasta Linziin
Keplerin vuodet Prahassa olivat verrattain rauhallisia ja tieteellisesti erittäin tuottavia. Itse asiassa, vaikka asiat menivät huonosti, hän ei näytä koskaan antaneen ulkoisten olosuhteiden estää häntä jatkamasta työtään. Asiat alkoivat mennä hyvin huonosti vuoden 1611 lopulla. Ensinnäkin hänen seitsemänvuotias poikansa kuoli. Kepler kirjoitti ystävälleen, että tätä kuolemaa oli erityisen vaikea kestää, koska lapsi muistutti häntä niin paljon itsestään tuon ikäisenä. Sitten Keplerin vaimo kuoli. Sitten keisari Rudolf, jonka terveys heikkeni, joutui luopumaan vallasta veljensä Matiaksen hyväksi, joka oli Rudolfin tavoin katolilainen, mutta joka (toisin kuin Rudolf) ei uskonut protestanttien suvaitsemiseen. Keplerin oli lähdettävä Prahasta. Ennen lähtöään hän siirrätti vaimonsa ruumiin pojan hautaan ja kirjoitti heille latinankielisen epitafin. Hän muutti jäljelle jääneine lapsineen Linziin (nykyään Itävallassa).
Avioliitto ja viinitynnyrit
Kepler näyttää menneen naimisiin ensimmäisen vaimonsa Barbaran kanssa rakkaudesta (vaikka avioliitto järjestettiin välittäjän kautta). Toinen avioliitto vuonna 1613 oli käytännön pakko; hän tarvitsi jonkun huolehtimaan lapsista. Keplerin uusi vaimo Susanna sai pikakurssin Keplerin luonteesta: syntyneen kirjan omistuskirjeessä kerrotaan, että Kepler huomasi hääjuhlissa, että viinitynnyreiden tilavuudet arvioitiin tikun avulla, joka pujotettiin vinosti tynnyrissä olevan reiän läpi, ja hän alkoi ihmetellä, miten se voi toimia. Tuloksena oli tutkimus kiertokappaleiden tilavuuksista Nova stereometria doliorum … Ⓣ, Linz, 1615, jossa Kepler käytti Arkhimedeen työhön tukeutuen ratkaisua ”jakamattomiin”. Tätä menetelmää kehitti myöhemmin Bonaventura Cavalieri (n. 1598 – 1647), ja se on osa infinitesimaalilaskennan esi-isää.
Maailman harmonia
Keplerin päätehtävä keisarillisena matemaatikkona oli kirjoittaa tähtitieteellisiä taulukoita, jotka perustuivat Tychon havaintoihin, mutta todellisuudessa hän halusi kirjoittaa teoksen Maailman harmonia, jota hän suunnitteli vuodesta 1599 lähtien kehitelläkseen teoksensa Kosmoksen mysteeri. Tässä toisessa kosmologiaa käsittelevässä teoksessa (Harmonices mundi libri V Ⓣ, Linz, 1619) esitellään aiempaa teosta kehittyneempi matemaattinen malli, vaikka moniulotteisuus on edelleen tallella. The Harmony of the World sisältää myös niin sanotun Keplerin kolmannen lain, jonka mukaan minkä tahansa kahden planeetan jaksojen neliöiden suhde on sama kuin niiden kiertoratojen keskisäteiden kuutioiden suhde. Kepler oli ensimmäisestä lähtien etsinyt sääntöä, joka liittäisi kiertoratojen koot jaksoihin, mutta tätä lakia kohti ei edetty hitaasti, kuten kahta muuta lakia kohti. Vaikka kolmannella lailla on tärkeä osa Maailman harmonia -teoksen painetun version joissakin loppuosissa, se löydettiin vasta, kun teos oli jo painossa. Kepler teki viime hetken tarkistuksia. Hän itse kertoo tarinan lopullisesta onnistumisesta:
…ja jos haluatte tarkan ajankohdan, niin se ideoitiin henkisesti 8. maaliskuuta tänä vuonna tuhat kuusisataakahdeksantoista, mutta esitettiin laskelmille epäonnisella tavalla ja hylättiin sen vuoksi vääränä, ja lopulta se palasi toukokuun 15. päivänä ja omaksuen uuden linjan hyökkäyksen, ryntäsi mieleni pimeyteen. Seitsemäntoista vuotta kestäneen työhöni Brahen havaintojen parissa tekemäni työn ja tämän tutkimuksen yhteenliittymä antoi niin vahvan tuen, että aluksi uskoin näkeväni unta ja olettaneeni johtopäätökseni perusolettamusteni joukkoon. Mutta on ehdottoman varmaa ja täsmällistä, että ”minkä tahansa kahden planeetan jaksoaikojen välinen suhde on täsmälleen niiden keskietäisyyksien seeskviaalinen suhde …”
(Harmonice mundi 5. kirja, 3. luku, suomennos Aiton, Duncan ja Field, s. 411).”
Noituusoikeudenkäynti
Keplerin työskennellessä Maailman harmonian parissa hänen äitiään syytettiin noituudesta. Hän turvautui Tübingenin oikeustieteellisen tiedekunnan apuun. Katharina Kepler vapautettiin lopulta, ainakin osittain teknisten vastaväitteiden vuoksi, jotka johtuivat siitä, että viranomaiset eivät noudattaneet oikeita oikeudellisia menettelyjä kidutuksen käytössä. Säilyneet asiakirjat ovat kylmääviä. Kepler jatkoi kuitenkin työtään. Matkalla Württembergiin puolustaakseen äitiään hän luki vaunuissa Vincenzo Galilein (n. 1520 – 1591, Galileon isä) musiikkiteoriaa käsittelevää teosta, johon on lukuisia viittauksia teoksessa The Harmony of the World.
Astronomical Tables
Taulukoiden laskeminen, tähtitieteilijän normaali työtehtävä, sisälsi aina raskasta aritmetiikkaa. Niinpä Kepler ilahtui, kun hän vuonna 1616 törmäsi Napierin logaritmeja käsittelevään (vuonna 1614 julkaistuun) teokseen. Mästlin sanoi hänelle kuitenkin heti, että vakavasti otettavan matemaatikon oli sopimatonta iloita pelkästä laskutoimituksen apuvälineestä ja että logaritmeihin ei ollut viisasta luottaa, koska kukaan ei ymmärtänyt, miten ne toimivat. (Samanlaisia kommentteja esitettiin tietokoneista 1960-luvun alussa.) Keplerin vastaus jälkimmäiseen vastalauseeseen oli julkaista logaritmien toiminnasta todiste, joka perustui moitteettomasti luotettavaan lähteeseen: Eukleideen elementtien kirjaan 5. Kepler laski kahdeksannumeroiset logaritmitaulukot, jotka julkaistiin Rudolphine Tables -teoksessa (Ulm, 1628). Tähtitieteellisissä taulukoissa käytettiin Tychon havaintojen lisäksi myös Keplerin kahta ensimmäistä lakia. Kaikki tähtitieteelliset taulukot, joissa käytettiin uusia havaintoja, olivat tarkkoja ensimmäisten vuosien ajan julkaisemisen jälkeen. Rudolfin taulukoissa oli huomionarvoista se, että ne osoittautuivat tarkoiksi vuosikymmenien ajan. Ja kun vuosia kertyi yhä enemmän, taulukoiden jatkuvaa tarkkuutta pidettiin luonnollisesti argumenttina Keplerin lakien oikeellisuuden ja siten heliosentrisen tähtitieteen oikeellisuuden puolesta. Se, että Kepler täytti tylsän virallisen tehtävänsä keisarillisena matemaatikkona, johti hänen hartaimman toiveensa täyttymiseen, nimittäin siihen, että hän auttoi kopernikaanismin vakiinnuttamisessa.
Wallenstein
Kun Rudolfin taulukot julkaistiin, Kepler ei itse asiassa enää työskennellyt keisarille (hän oli lähtenyt Linzistä vuonna 1626), vaan Albrecht von Wallensteinille (1583 – 1632), joka oli yksi harvoista menestyneistä sotilasjohtajista kolmikymmenvuotisessa sodassa (1618 – 1648).
Wallenstein odotti keisari Rudolfin tavoin, että Kepler antaisi hänelle astrologiaan perustuvia neuvoja. Keplerin oli luonnollisesti toteltava, mutta huomauttaa toistuvasti, ettei hän usko tarkkojen ennusteiden tekemiseen. Useimpien aikalaisten tavoin Kepler hyväksyi astrologian periaatteen, jonka mukaan taivaankappaleet voivat vaikuttaa siihen, mitä maapallolla tapahtuu (selkeimpinä esimerkkeinä Aurinko aiheuttaa vuodenajat ja Kuu vuoroveden), mutta kopernikaanisena hän ei uskonut tähtikuvioiden fyysiseen todellisuuteen. Hänen astrologiansa perustui ainoastaan taivaankappaleiden asemien välisiin kulmiin (”astrologiset aspektit”). Hän ilmaisee täydellisen halveksuntansa perinteisen astrologian monimutkaisia järjestelmiä kohtaan.
Kuolema
Kepler kuoli Regensburgissa lyhyen sairauden jälkeen. Hän yöpyi kaupungissa matkalla noutamaan rahaa, joka oli hänelle velkaa Rudolfin taulukoihin liittyen. Hänet haudattiin paikalliseen kirkkoon, mutta se tuhoutui kolmikymmenvuotisen sodan aikana, eikä haudasta ole jäljellä mitään.
Historiografinen huomautus
Keplerin tieteellisen toiminnan oletetuista ei-rationaalisista elementeistä on toisinaan puhuttu paljon. Uskovaiset astrologit väittävät usein, että hänen työnsä tarjoaa tieteellisesti varteenotettavan esiasteen heidän omalle työlleen. Edesmennyt Arthur Koestler teki vaikutusvaltaisessa teoksessaan Sleepwalkers (Unissakävelijät) Keplerin taistelusta Marsin kanssa argumentin modernin tieteen luontaisen irrationaalisuuden puolesta. Näillä kahdella vakaumuksella on ollut monia hiljaisia seuraajia. Molemmat perustuvat kuitenkin Keplerin työn hyvin osittaiseen lukemiseen. Erityisesti Koestlerilla ei näytä olleen riittävää matemaattista asiantuntemusta Keplerin menettelytapojen ymmärtämiseen. Lähempi tarkastelu osoittaa, että Koestler yksinkertaisesti erehtyi arviossaan.
Todella tärkeä ei-rationaalinen elementti Keplerin työssä on hänen kristinuskonsa. Keplerin laaja ja menestyksekäs matematiikan käyttö saa hänen työnsä näyttämään ”modernilta”, mutta itse asiassa kyseessä on kristitty luonnonfilosofi, jolle maailmankaikkeuden luonteen ymmärtämiseen kuului myös sen Luojan luonteen ymmärtäminen.