Kaltevuuden ja leikkauspisteen muodossa oleva yhtälö kirjoitetaan seuraavasti:
$$y=mx+b$$$
Jossa m on suoran kaltevuus ja b on y-kohta. Voit käyttää tätä yhtälöä yhtälön kirjoittamiseen, jos tiedät kaltevuuden ja y-pisteen.
Esimerkki
Etsitään suoran yhtälö
Valitaan kaksi pistettä, jotka ovat suoralla
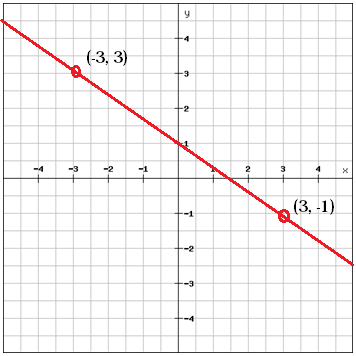
Lasketaan näiden kahden pisteen välinen kaltevuus
$$m=\\frac{y_{2}\, -y_{1}}}{x_{2}\, -x_{1}}=\frac{\left (-1 \right )-3}{3-\left ( -3 \right )}=\frac{-4}{6}=\frac{-2}{3}$$
Voidaan löytää b-arvo, y-suuntaviivan, tarkastelemalla kuvaajaa
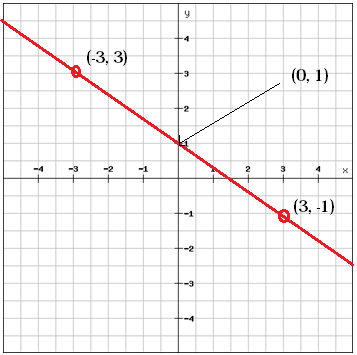
b = 1
Meillä on arvo m:lle ja arvo b:lle. Näin saamme lineaarisen funktion
$$y=-\frac{2}{3}x+1$$
Monissa tapauksissa b:n arvo ei ole yhtä helposti luettavissa. Näissä tapauksissa, tai jos olet epävarma siitä, ylittääkö suora todella y-akselin tässä nimenomaisessa pisteessä, voit laskea b:n ratkaisemalla yhtälön b:n suhteen ja korvaamalla x:n ja y:n jollakin kahdesta pisteestäsi.
Voidaan käyttää yllä olevaa esimerkkiä havainnollistamaan tätä. Meillä on kaksi pistettä (-3, 3) ja (3, -1). Näistä kahdesta pisteestä laskimme kaltevuuden
$$m=-\frac{2}{3}$$$
Tästä saamme yhtälön
$$y=-\frac{2}{3}x+b$$
Tästä voimme ratkaista yhtälön b:n suhteen
$$$b=y+\frac{2}{3}x$$$
Ja jos laitamme ensimmäisestä pisteestämme saadut arvot (-3, 3) saamme
$$b=3+\frac{2}{3}\cdot \left ( -3 \right )=3+\left ( -2 \right )=1$$$
Jos laitamme tämän b:n arvon yhtälöön, saamme
$$y=-\frac{2}{3}x+1$$$
joka on sama yhtälö, jonka saimme, kun luimme kuvaajasta y-välin.
Yhteenvetona siitä, miten lineaarinen yhtälö kirjoitetaan käyttäen kaltevuus-intercept-muotoa, voit
- Tunnistaa kaltevuuden, m. Tämä voidaan tehdä laskemalla kaltevuus kahden tunnetun suoran pisteen välillä kaltevuuskaavalla.
- Löydät y-interceptin. Tämä voidaan tehdä korvaamalla kaltevuus ja suoran pisteen (x, y) koordinaatit kaltevuuden ja leikkauspisteen kaavalla ja ratkaisemalla sitten b.
Kun olet saanut sekä m:n että b:n, voit vain laittaa ne yhtälöön omalle paikalleen.
Videon oppitunti
Erittäkää kuvaajan yhtälö
yhtälön yhtälö.