Rovnice ve tvaru s úsečkou se zapisuje jako
$$y=mx+b$$
Kde m je sklon přímky a b je úsečka y. Tuto rovnici můžete použít k zápisu rovnice, pokud znáte sklon a y-intercept.
Příklad
Najděte rovnici přímky
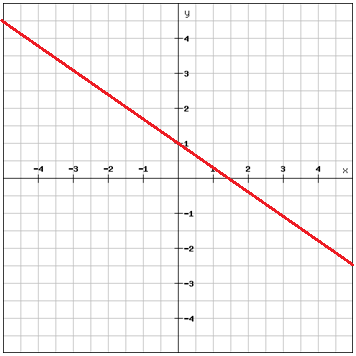
Vyberte dva body, které leží na přímce
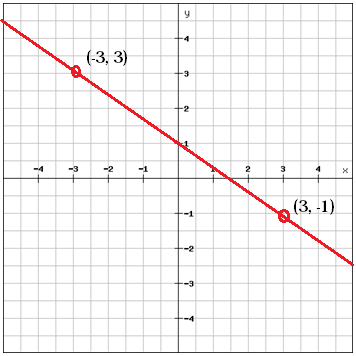
Vypočítejte sklon mezi těmito dvěma body
$$m=\frac{y_{2}\, -y_{1}}{x_{2}\, -x_{1}}=\frac{\levá (-1 \pravá )-3}{3-\levá ( -3 \pravá )}=\frac{-4}{6}=\frac{-2}{3}$$
Můžeme zjistit hodnotu b, y-intercepci, pohledem na graf
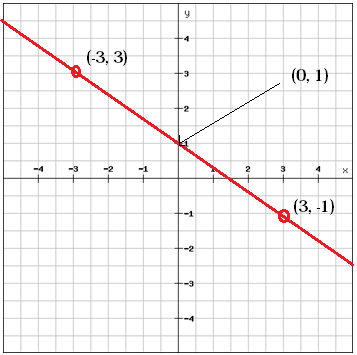
b = 1
Máme hodnotu m a hodnotu b. Tím získáme lineární funkci
$$y=-\frac{2}{3}x+1$$
V mnoha případech není hodnota b tak snadno čitelná. V těchto případech, nebo pokud si nejste jisti, zda přímka skutečně protíná osu y v tomto konkrétním bodě, můžete vypočítat b tak, že vyřešíte rovnici pro b a poté nahradíte x a y jedním z vašich dvou bodů.
Pro ilustraci můžeme použít výše uvedený příklad. Máme dva body (-3, 3) a (3, -1). Z těchto dvou bodů jsme vypočítali sklon
$$m=-\frac{2}{3}$$
Tím jsme získali rovnici
$$y=-\frac{2}{3}x+b$$
Z toho můžeme vyřešit rovnici pro b
$b=y+\frac{2}{3}x$$
A když dosadíme hodnoty z našeho prvního bodu (-3, 3) dostaneme
$$b=3+\frac{2}{3}\cdot \left ( -3 \right )=3+\left ( -2 \right )=1$$
Pokud dosadíme tuto hodnotu b do rovnice, dostaneme
$$y=-\frac{2}{3}x+1$$
což je stejná rovnice, jakou jsme dostali, když jsme z grafu odečetli y-intercept.
Pro shrnutí, jak zapsat lineární rovnici pomocí tvaru sklon-intercept, je třeba
- určit sklon, m. To lze provést výpočtem sklonu mezi dvěma známými body přímky pomocí vzorce pro sklon.
- Najít y-intercept. To lze provést dosazením sklonu a souřadnic bodu (x, y) na přímce do vzorce pro sklon a průsečík a následným řešením pro b.
Jakmile získáte m i b, stačí je dosadit do rovnice na příslušné místo.
Video lekce
Najděte rovnici ke grafu
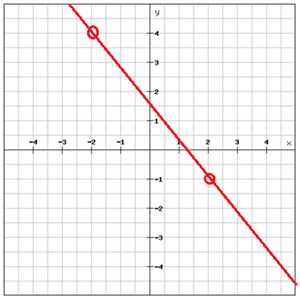
.