Selekční třídění – algoritmus, zdrojový kód, časová složitost

Tento článek je součástí seriálu „Třídicí algoritmy:

• popisuje, jak Selection Sort funguje,
• obsahuje zdrojový kód jazyka Java pro Selection Sort,
• ukazuje, jak odvodit jeho časovou složitost (bez složité matematiky)
• a ověřuje, zda výkon implementace v jazyce Java odpovídá očekávanému chování za běhu.

Zdrojový kód celé série článků najdete v mém repozitáři GitHub.

Příklad:

Třídění hracích karet

Třídění hracích karet do ruky je klasickým příkladem pro Insertion Sort.

Selekční třídění lze také ilustrovat pomocí hracích karet. Neznám nikoho, kdo by si tímto způsobem vybíral karty, ale jako příklad to funguje docela dobře 😉

Nejprve položíte všechny karty lícem nahoru na stůl před sebe. Vyhledáte nejmenší kartu a vezmete si ji do levé části ruky. Pak vyhledáš další větší kartu a položíš ji napravo od nejmenší karty, a tak dále, až nakonec vezmeš největší kartu úplně vpravo.

Rozdíl oproti Třídění vkládáním

Při Třídění vkládáním jsme vzali další nevytříděnou kartu a vložili ji na správné místo mezi vytříděné karty.

Třídění výběrem funguje tak trochu obráceně:

Algoritmus výběrového třídění

Algoritmus lze nejjednodušeji vysvětlit na příkladu. V následujících krocích ukážu, jak seřadit pole pomocí Selection Sort:

Krok 1

Pole rozdělíme na levou, seřazenou část a pravou, neseřazenou část. Seřazená část je na začátku prázdná:

Krok 2

V pravé, neseřazené části hledáme nejmenší prvek. K tomu si nejprve zapamatujeme první prvek, kterým je 6. Přejdeme na další pole, kde najdeme ještě menší prvek 2. Projdeme zbytek pole a hledáme ještě menší prvek. Protože žádný nenajdeme, zůstaneme u prvku 2. Umístíme ho na správnou pozici tak, že ho prohodíme s prvkem na prvním místě. Pak posuneme hranici mezi částmi pole o jedno pole doprava:

Krok 3

Znovu hledáme v pravé, nesetříděné části nejmenší prvek. Tentokrát je to trojka; prohodíme ji s prvkem na druhé pozici:

Krok 4

Znovu hledáme nejmenší prvek v pravé části. Je to 4, který je již na správné pozici. V tomto kroku tedy není třeba provádět operaci prohození a pouze posuneme hranici úseku:

Krok 5

Jako nejmenší prvek nalezneme šestku. Prohodíme jej s prvkem na začátku pravé části, tedy s 9:

Krok 6

Ze zbývajících dvou prvků je nejmenší prvek 7. Prohodíme ho s 9:

Algoritmus dokončen

Poslední prvek je automaticky největší, a proto na správném místě. Algoritmus je dokončen a prvky jsou seřazeny:

Zdrojový kód Selection Sort v jazyce Java

V této části najdete jednoduchou implementaci Selection Sort v jazyce Java.

Vnější smyčka iteruje nad prvky, které mají být seřazeny, a končí za předposledním prvkem. Jakmile je tento prvek setříděn, je automaticky setříděn i poslední prvek. Proměnná smyčky i vždy ukazuje na první prvek pravé, netříděné části.

V každém cyklu smyčky se za první prvek pravé části zpočátku považuje nejmenší prvek min; jeho pozice je uložena v minPos.

Vnitřní cyklus pak iteruje od druhého prvku pravé části k jejímu konci a přerozděluje min a minPos vždy, když je nalezen ještě menší prvek.

Po dokončení vnitřního cyklu jsou prvky na pozicích i (začátek pravé části) a minPos prohozeny (pokud se nejedná o stejný prvek).

public class SelectionSort { public static void sort(int elements) { int length = elements.length; for (int i = 0; i < length - 1; i++) { // Search the smallest element in the remaining array int minPos = i; int min = elements; for (int j = i + 1; j < length; j++) { if (elements < min) { minPos = j; min = elements; } } // Swap min with element at pos i if (minPos != i) { elements = elements; elements = min; } } }}

Zobrazený kód se od třídy SelectionSort v repozitáři GitHub liší tím, že implementuje rozhraní SortAlgorithm, aby byl snadno zaměnitelný v rámci testovacího frameworku.

Časová složitost třídění výběru

Značíme n počet prvků, v našem příkladu n = 6.

Dvě vnořené smyčky naznačují, že máme co do činění s časovou složitostí* O(n²). Bude tomu tak v případě, že obě smyčky iterují k hodnotě, která lineárně roste s n.

To je zřejmě případ vnější smyčky: počítá se až do n-1.

A co vnitřní smyčka?

Podívejte se na následující obrázek:

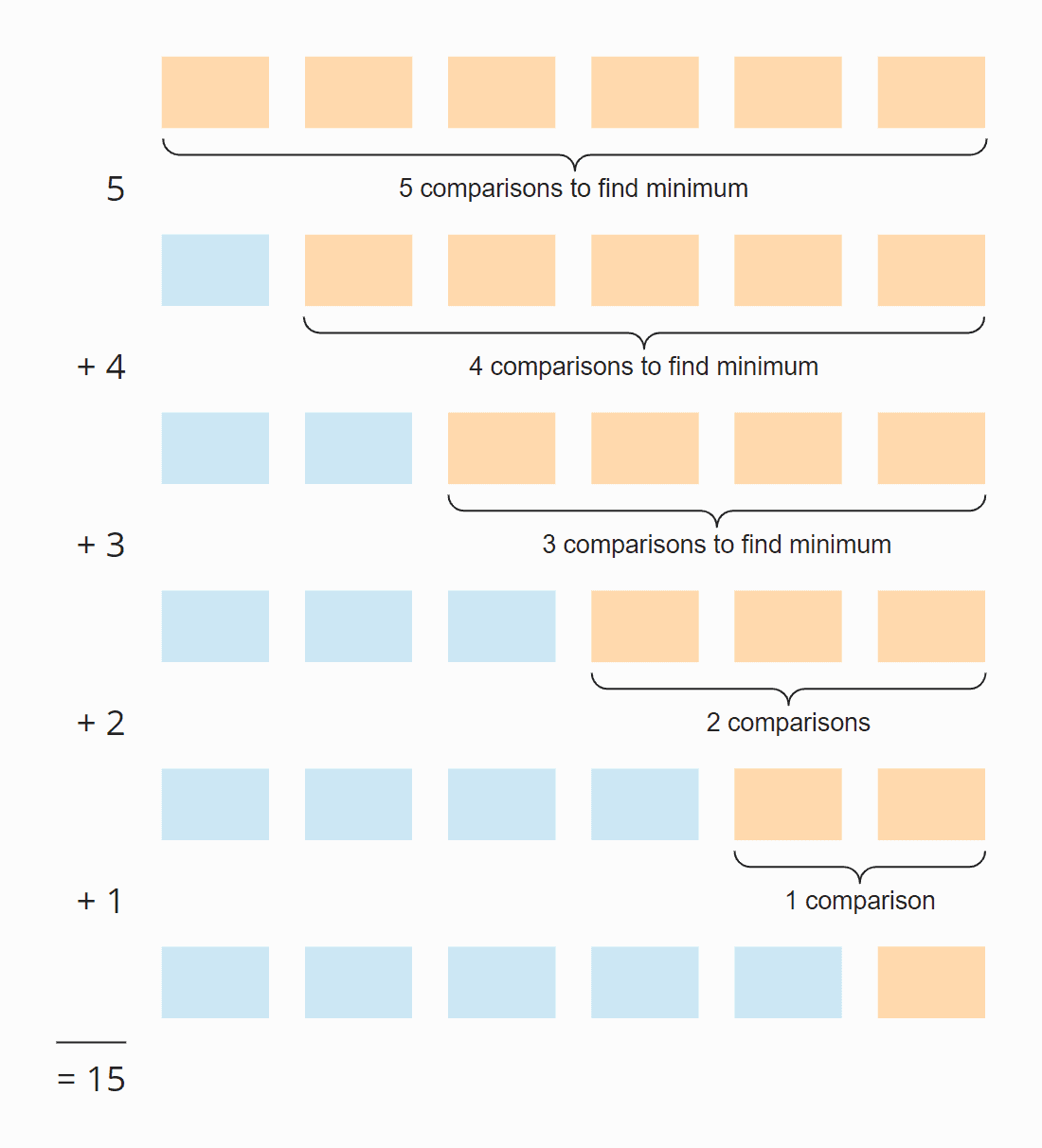
V každém kroku je počet porovnání o jedna menší než počet nesetříděných prvků. Celkem je tedy provedeno 15 porovnání – bez ohledu na to, zda je pole na počátku setříděno, nebo ne.

To lze také vypočítat takto:

Šest prvků krát pět kroků; děleno dvěma, protože v průměru za všechny kroky je polovina prvků stále ještě neutříděná:

6 × 5 × ½ = 30 × ½ = 15

Nahradíme-li 6 za n, dostaneme

n × (n – 1) × ½

Po vynásobení je to:

½ n² – ½ n

Nejvyšší mocnina n v tomto členu je n². Časová složitost hledání nejmenšího prvku je tedy O(n²) – říká se jí také „kvadratický čas“.

Podívejme se nyní na prohození prvků. V každém kroku (kromě posledního) se prohodí buď jeden prvek, nebo žádný, podle toho, zda je nejmenší prvek již na správné pozici, nebo ne. V součtu tedy máme maximálně n-1 operací prohození, tj. časovou složitost O(n) – říká se jí také „lineární čas“.

Pro celkovou složitost je důležitá pouze nejvyšší třída složitosti, proto:

Průměrná, nejlepší a nejhorší časová složitost Selection Sort je: O(n²)

* Pojmy „časová složitost“ a „O-notace“ jsou v tomto článku vysvětleny na příkladech a schématech.

Čas běhu příkladu Selection Sort v Javě

Teorie už bylo dost! Napsal jsem testovací program, který měří dobu běhu Selekčního třídění (a všech ostatních třídicích algoritmů, o nichž pojednává tento seriál) takto:

• Počet prvků, které je třeba seřadit, se po každé iteraci zdvojnásobí z původních 1 024 prvků na 536 870 912 (= 229) prvků. Pole o dvojnásobné velikosti nelze v Javě vytvořit.
• Pokud test trvá déle než 20 sekund, pole se dále nerozšiřuje.
• Všechny testy jsou prováděny s nesetříděnými i vzestupně a sestupně předtříděnými prvky.
• Povolujeme překladači HotSpot optimalizovat kód pomocí dvou zahřívacích kol. Poté se testy opakují, dokud není proces přerušen.

Po každé iteraci program vypíše medián všech předchozích výsledků měření.

Tady je výsledek pro Selekční třídění po 50 iteracích (pro přehlednost je to jen výňatek, kompletní výsledek najdete zde):

n	nesetříděné	vzestupné	sestupné
….	…	…	…
16,384	27,9 ms	26,8 ms	65,6 ms
32.768	108,0 ms	105,4 ms	265,4 ms
65.536	434,0 ms	424,3 ms	1.052,2 ms
131.072	1.729,8 ms	1.714,1 ms	4.209,9 ms
262.144	6.913,4 ms	6.880,2 ms	16.863,7 ms
524.288	27.649,8 ms	27.568,7 ms	67.537,8 ms

Tady měření ještě jednou jako graf (přičemž „neseřazené“ a „vzestupné“ jsem zobrazil jako jednu křivku kvůli téměř shodným hodnotám):

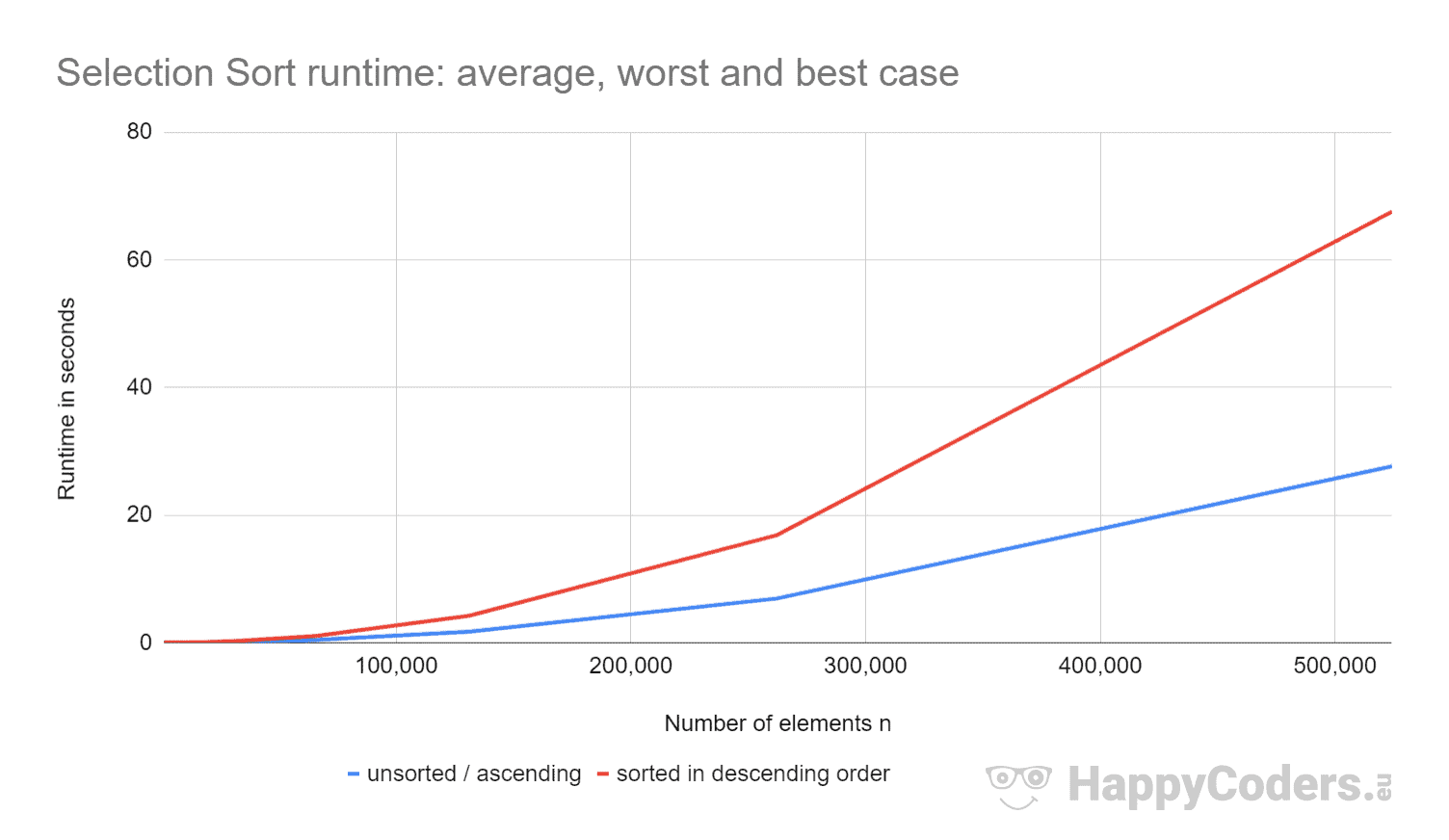
Je dobře vidět, že

• při zdvojnásobení počtu prvků se doba běhu přibližně zečtyřnásobí – bez ohledu na to, zda jsou prvky předem setříděné nebo ne. To odpovídá očekávané časové složitosti O(n²).
• že doba běhu pro vzestupně seřazené prvky je o něco lepší než pro nesetříděné prvky. Je to proto, že operace prohození, které – jak bylo analyzováno výše – nemají velký význam, zde nejsou nutné.
• že doba běhu pro sestupně seřazené prvky je výrazně horší než pro nesetříděné prvky.

Proč tomu tak je?

Analýza doby běhu v nejhorším případě

Teoreticky by hledání nejmenšího prvku mělo trvat vždy stejně dlouho bez ohledu na výchozí situaci. A operací výměny by mělo být jen o něco více pro prvky seřazené sestupně (u prvků seřazených sestupně by se musel vyměnit každý prvek; u neseřazených prvků by se musel vyměnit téměř každý prvek).

Pomocí programu CountOperations z mého repozitáře GitHub můžeme zjistit počet různých operací. Zde jsou výsledky pro nesetříděné prvky a prvky seřazené sestupně, shrnuté v jedné tabulce:

n	Srovnání	Směny nesetříděné	Směny sestupně	Směny seřazené	minPos/min nesetříděné	minPos/min sestupné
…	…	…	…	…	…
512	130.816	504	256	2.866	66.047
1.024	523.776	1.017	512	6.439	263.167
2.048	2.096.128	2.042	1.024	14.727	1.050.623
4.096	8.386.560	4.084	2.048	30.758	4.198.399
8.192	33.550.336	8.181	4.096	69.378	16.785.407

Z naměřených hodnot lze vyčíst:

• Při sestupně seřazených prvcích máme – podle očekávání – tolik porovnávacích operací jako při neseřazených prvcích – tedy n × (n-1) / 2. V případě, že je prvek seřazen sestupně, je počet porovnávacích operací stejný.
• S neuspořádanými prvky máme – podle předpokladu – téměř tolik operací prohození jako s prvky: například s 4 096 neuspořádanými prvky je 4 084 operací prohození. Tato čísla se náhodně mění test od testu.
• S prvky seřazenými sestupně však máme jen o polovinu méně výměnných operací než prvků! Je to proto, že při prohození dáváme na správné místo nejen nejmenší prvek, ale také příslušného prohozeného partnera.

Příklad při osmi prvcích máme čtyři prohozené operace. V prvních čtyřech iteracích máme po jedné a v iteracích pět až osm žádnou (přesto algoritmus běží dál až do konce):

Dále můžeme z měření vyčíst:

• Důvod, proč je Selection Sort o tolik pomalejší s prvky seřazenými sestupně, lze najít v počtu přiřazení lokálních proměnných (minPos a min) při hledání nejmenšího prvku. Zatímco u 8 192 nesetříděných prvků máme 69 378 těchto přiřazení, u prvků setříděných sestupně je takových přiřazení 16 785 407 – to je 242krát více!“

Proč tento obrovský rozdíl?“

Analýza doby běhu hledání nejmenšího prvku

Pro prvky setříděné sestupně lze řádovou velikost odvodit z obrázku právě uvedeného výše. Hledání nejmenšího prvku je omezeno na trojúhelník oranžových a oranžovomodrých políček. V horní oranžové části se čísla v jednotlivých rámečcích zmenšují; v pravé oranžovomodré části se čísla opět zvětšují.

V každém oranžovém políčku a v prvním z oranžovomodrých políček probíhají přiřazovací operace. Počet přiřazovacích operací pro minPos a min je tedy, obrazně řečeno, asi „čtvrtina čtverce“ – matematicky a přesně je to ¼ n² + n – 1.

Pro nesetříděné prvky bychom museli do věci proniknout mnohem hlouběji. To by přesahovalo nejen rámec tohoto článku, ale i celého blogu.

Omezím se proto na malý demonstrační program, který změří, kolik je přiřazení minPos/min při hledání nejmenšího prvku v nesetříděném poli. Zde jsou průměrné hodnoty po 100 iteracích (malý výtah; kompletní výsledky najdete zde):

n	průměrný počet minPos/min přiřazení
1.024	7.08
4.096	8.61
16.385	8.94
65.536	11.81
262.144	12.22
1.048.576	14.26
4.194.304	14.71
16.777.216	16.44
67.108.864	17.92
268.435.456	20.27

Zde jako graf s logaritmickou osou x:

Kartogram velmi pěkně ukazuje, že máme logaritmický růst, tj, že s každým zdvojnásobením počtu prvků se počet přiřazení zvyšuje pouze o konstantní hodnotu. Jak jsem řekl, nebudu se hlouběji zabývat matematickým pozadím.

To je důvod, proč tato přiřazení minPos/min nemají v netříděných polích velký význam.

Další vlastnosti selekčního třídění

V následujících částech se budu zabývat prostorovou složitostí, stabilitou a paralelizovatelností selekčního třídění.

Prostorová složitost Selection Sort

Prostorová složitost Selection Sort je konstantní, protože kromě smyčkových proměnných i a j a pomocných proměnných length, minPos a min nepotřebujeme žádný další paměťový prostor.

To znamená, že bez ohledu na to, kolik prvků třídíme – deset nebo deset milionů – potřebujeme vždy jen těchto pět dalších proměnných. Konstantní čas zaznamenáváme jako O(1).

Stabilita výběrového třídění

Výběrové třídění se na první pohled zdá být stabilní:

Ale zdání klame. Protože prohozením dvou prvků ve druhém dílčím kroku algoritmu se může stát, že některé prvky v neutříděné části již nebudou mít původní pořadí. To zase vede k tomu, že v setříděné části se již neobjevují v původním pořadí.

Příklad lze zkonstruovat velmi jednoduše. Předpokládejme, že máme dva různé prvky s klíčem 2 a jeden s klíčem 1, uspořádané následujícím způsobem, a pak je seřadíme pomocí Selection Sort:

V prvním kroku se prohodí první a poslední prvek. Prvek „DVA“ tak skončí za prvkem „dva“ – pořadí obou prvků se prohodí.

V druhém kroku algoritmus porovná oba zadní prvky. Oba mají stejný klíč, 2. Žádný prvek tedy není prohozen.

Ve třetím kroku zůstává pouze jeden prvek; ten je automaticky považován za setříděný.

Dva prvky s klíčem 2 tedy byly prohozeny na své původní pořadí – algoritmus je nestabilní.

Stabilní varianta výběrového třídění

Výběrové třídění lze učinit stabilním tak, že ve druhém kroku nepřehodíme nejmenší prvek s prvním, ale posuneme všechny prvky mezi prvním a nejmenším prvkem o jednu pozici doprava a nejmenší prvek vložíme na začátek.

Přestože časová složitost zůstane díky této změně stejná, dodatečné posuny povedou k výraznému snížení výkonu, alespoň pokud třídíme pole.

Při použití spojového seznamu bychom mohli vyjmutí a vložení prvku, který má být setříděn, provést bez výrazné ztráty výkonu.

Paralelizovatelnost výběrového třídění

Vnější smyčku nemůžeme paralelizovat, protože v každé iteraci mění obsah pole.

Vnitřní smyčku (hledání nejmenšího prvku) lze paralelizovat rozdělením pole, paralelním hledáním nejmenšího prvku v každém dílčím poli a sloučením mezivýsledků.

Selekční třídění vs. vkládací třídění

Který algoritmus je rychlejší, Selekční třídění, nebo vkládací třídění?

Srovnejme měření z mých implementací v Javě.

Vynechám nejlepší případ. U Insertion Sort je časová složitost v nejlepším případě O(n) a trvala méně než milisekundu až pro 524 288 prvků. V nejlepším případě je tedy Insertion Sort pro libovolný počet prvků řádově rychlejší než Selection Sort.

n	Selekční třídění nesetříděné	Vložené třídění nesetříděné	Selekční třídění sestupné	Vložené třídění sestupné
…	….	…	…	…
16.384	27,9 ms	21,9 ms	65,6 ms	43,6 ms
32.768	108,0 ms	87,9 ms	265,4 ms	175,8 ms
65,536	434,0 ms	350,4 ms	1.052,2 ms	697,6 ms
131.072	1.729,8 ms	1.398,9 ms	4.209,9 ms	2.840,0 ms
262.144	6.913,4 ms	5.706,8 ms	16.863,7 ms	11.517,4 ms
524.288	27.649,8 ms	23.009,7 ms	67.537,8 ms	46.309,3 ms

A ještě jednou jako graf:

Insertion Sort je tedy rychlejší než Selection Sort nejen v nejlepším, ale i v průměrném a nejhorším případě.

Důvodem je to, že Insertion Sort vyžaduje v průměru o polovinu méně porovnání. Pro připomenutí, u Insertion Sort máme porovnání a posuny v průměru až poloviny setříděných prvků; u Selection Sort musíme v každém kroku hledat nejmenší prvek ve všech nesetříděných prvcích.

Selection Sort má výrazně méně operací zápisu, takže Selection Sort může být rychlejší, když jsou operace zápisu drahé. To neplatí pro sekvenční zápisy do polí, protože ty se většinou provádějí v mezipaměti procesoru.

V praxi se proto Selection Sort téměř nepoužívá.

Shrnutí

Selection Sort je snadno implementovatelný a ve své typické implementaci nestabilní třídicí algoritmus s průměrnou, nejlepší i nejhorší časovou složitostí O(n²).

Selection Sort je pomalejší než Insertion Sort, proto se v praxi používá jen zřídka.

Další třídicí algoritmy najdete v tomto přehledu všech třídicích algoritmů a jejich vlastností v prvním díle série článků.

Pokud se vám článek líbil, neváhejte jej sdílet pomocí některého z tlačítek pro sdílení na konci. Chcete být informováni e-mailem, když vydám nový článek? Pak se pomocí následujícího formuláře přihlaste k odběru mého newsletteru.

.