Příroda, zlatý řez a Fibonacciho čísla …

Rostliny mohou pěstovat nové buňky ve spirálách, jako je například vzor semen v této krásné slunečnici.

Ke spirále dochází přirozeně, protože každá nová buňka vzniká po otočení.

„Nová buňka, pak otočení,
poté další buňka, pak otočení, …“

Jak daleko se otočit?

Takže, kdybyste byli rostlinou, jak moc byste se otáčeli mezi novými buňkami?“

Pokud se neotáčíte vůbec, dostanete rovnou čáru.

To je ale velmi špatný návrh .. chcete něco kulatého, co bude držet pohromadě bez mezer.

Proč nezkusíte najít pro sebe nejlepší hodnotu?

Zkoušejte různé hodnoty, například 0,75, 0,9, 3,1416, 0,62 atd.

Pamatujte, že se snažíte vytvořit obrazec bez mezer od začátku do konce:

(Mimochodem, nezáleží na celé části čísla, jako je 1. nebo 5., protože jsou to plné otáčky, které nás směřují zpět stejným směrem.)

Co jsi dostal?“

Pokud jsi dostal něco, co končí jako 0,618 (nebo 0,382, což je 1 – 0,618), pak „Gratuluji, jsi úspěšným členem rostlinné říše!“

To proto, že zlatý řez (1. Zlatý řez) je v tomto případě stejný.61803…) je nejlepším řešením a slunečnice na to přišla svým vlastním přirozeným způsobem. Zkuste to … mělo by to vypadat takto.

Proč?“

Každé číslo, které je jednoduchým zlomkem (příklad: 0….75 je 3/4 a 0,95 je 19/20 atd.) bude po chvíli vytvářet vzor čar, které se budou skládat na sebe, čímž vzniknou mezery.

Ale zlatý řez (jeho symbolem je řecké písmeno Phi, na obrázku vlevo) je expert na to, že není žádným zlomkem.

Je to iracionální číslo (to znamená, že ho nemůžeme zapsat jako prostý zlomek), ale co víc … je tak daleko, jak se jen můžeme dostat k tomu, aby bylo blízko jakémukoli zlomku.

Jak tedy funguje zlatý řez?

Jednou ze zvláštních vlastností zlatého řezu je to, že jej lze definovat sám o sobě, například takto:
	(V číslech: 1,61803… = 1 + 1/1,61803….)
To lze rozvést na tento zlomek, který pokračuje donekonečna (říká se mu „pokračující zlomek“):

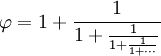Takto elegantně vklouzne mezi jednoduché zlomky.

Fibonacciho čísla

Mezi zlatým řezem a Fibonacciho čísly existuje zvláštní vztah (0, 1, 1, 2, 3, 5, 8, 13, 21, … atd. každé číslo je součtem dvou čísel před ním).

Pokud vezmeme libovolná dvě po sobě (za sebou) jdoucí Fibonacciho čísla, jejich poměr je velmi blízký zlatému řezu:

A	B		B / A
2	3		1.5
3	5		1.666666666…
5	8		1.6
8	13		1.625
13	21		1.615384615…
…	…		…
144	233		1.618055556…
233	377		1.618025751….
…	…		…

Takže stejně jako při použití 0 dostaneme přirozeně sedm ramen.142857 (1/7), máme tendenci dostávat Fibonacciho čísla, když použijeme zlatý řez.

Zkuste spočítat spirální ramena – spirály „točící se doleva“ a pak spirály „točící se doprava“ … jaká čísla jste dostali?

Spirálovitý růst listů

Toto zajímavé chování se nevyskytuje jen u slunečnicových semen.

Spirálovitě mohou růst i listy, větve a okvětní lístky.

Proč? Aby nové listy nebránily slunci před staršími listy nebo aby maximální množství deště nebo rosy směřovalo dolů ke kořenům.

Ve skutečnosti, když má rostlina spirály, bývá rotace zlomkem tvořeným dvěma po sobě (za sebou) jdoucími Fibonacciho čísly, například:

• Poloviční rotace je 1/2 (1 a 2 jsou Fibonacciho čísla)
• 3/5 je také běžná (obě Fibonacciho čísla) a
• 5/8 také (uhodli jste!)

vše se stále více blíží zlatému řezu.

A proto jsou Fibonacciho čísla v rostlinách velmi častá. 1, 2, 3, 5, 8, 13, 21, … atd. se vyskytují na úžasném množství míst. Tady je sedmikráska s 21 okvětními lístky (ale počítejte s tím, že jich bude o pár víc nebo míň, protože některé mohly odpadnout nebo teprve vyrůst)

Ale ne u všech rostlin se s tím setkáváme, protože příroda má mnoho různých způsobů přežití.

Zlatý úhel

Dosud jsme mluvili o „otočkách“ (plných otáčkách).

Evivalent 0,61803… otáček je 222,4922… stupňů, tedy asi 222,5°.

V opačném směru je to asi 137,5°, kterým se říká „zlatý úhel“.

Až se tedy příště budete procházet po zahradě, hledejte zlatý úhel,
a počítejte okvětní lístky a listy, abyste našli Fibonacciho čísla,
a zjistili, jak jsou rostliny chytré… !

Cvičení

Proč nejdete hned teď do zahrady nebo do parku a nezačnete počítat listy a okvětní lístky a měřit otáčky, abyste zjistili, co jste našli.

Své výsledky můžete zapsat do tohoto formuláře:

Jméno nebo popis rostliny:
Rostou listy ve spirálách? ANO / NE
Spočítejte skupinu listů:
	Kolik listů (a) ?
	Kolik plných otáček (b) ?
	Otočení na list (b/a) :
	Úhel otočení (360 × b/a) :
Existují květy? ANO / NE
	Kolik okvětních lístků má květ 1:
	Květ 2:
	Květ 3:		:

(Ale nezapomeňte, že příroda má svá vlastní pravidla a nemusí se řídit matematickými vzorci,
ale když se jimi řídí, je úžasné to vidět.)

.