Biografie
Johannes Kepler je dnes připomínán především díky objevu tří zákonů pohybu planet, které nesou jeho jméno a byly publikovány v letech 1609 a 1619.) Dále vykonal významné práce v optice (1604, 1611), objevil dva nové pravidelné mnohostěny (1619), podal první matematické pojednání o těsném uspořádání stejných koulí (což vedlo k vysvětlení tvaru buněk včelí plástve, 1611), podal první důkaz fungování logaritmů (1624) a vymyslel metodu zjišťování objemů rotačních těles, kterou lze (s odstupem času!) považovat za příspěvek k rozvoji kalkulu (1615, 1616). Kromě toho vypočítal dosud nejpřesnější známé astronomické tabulky, jejichž trvalá přesnost významně přispěla k potvrzení pravdivosti heliocentrické astronomie (Rudolfínské tabulky, Ulm, 1627).
Zachovalo se velké množství Keplerovy korespondence. Mnohé z jeho dopisů se téměř rovnají vědeckému článku (tehdy ještě neexistovaly vědecké časopisy) a zdá se, že korespondenti je uchovávali, protože byly zajímavé. V důsledku toho toho víme poměrně hodně o Keplerově životě a vlastně i o jeho charakteru. Částečně i díky tomu udělal Kepler jakousi kariéru víceméně fiktivní postavy (viz historiografická poznámka níže).
Dětství
Kepler se narodil v městečku Weil der Stadt ve Švábsku a v roce 1576 se s rodiči přestěhoval do nedalekého Leonbergu. Jeho otec byl námezdní voják a matka dcera hostinského. Johannes byl jejich prvním dítětem. Jeho otec opustil domov naposledy, když bylo Johannesovi pět let, a předpokládá se, že zahynul ve válce v Nizozemí. Jako dítě žil Kepler s matkou v dědečkově hostinci. Vypráví, že si vypomáhal službou v hostinci. Lze si představit, že zákazníci byli někdy zmateni neobvyklou schopností dítěte počítat.
Keplerovo rané vzdělání probíhalo v místní škole a poté v nedalekém semináři, z něhož se s úmyslem být vysvěcen nechal zapsat na univerzitu v Tübingenu, tehdy (stejně jako dnes) baště luteránské ortodoxie.
Keplerovy názory
Po celý život byl Kepler hluboce věřící člověk. Všechny jeho spisy obsahují četné zmínky o Bohu a svou práci považoval za naplnění křesťanské povinnosti porozumět Božím dílům. Jelikož byl člověk, jak Kepler věřil, stvořen k obrazu Božímu, byl zjevně schopen porozumět vesmíru, který stvořil. Kepler byl navíc přesvědčen, že Bůh stvořil vesmír podle matematického plánu (toto přesvědčení se objevuje v Platónových dílech a je spojováno s Pythagorem). Jelikož se v té době všeobecně uznávalo, že matematika poskytuje bezpečnou metodu, jak dospět k pravdám o světě (Euklidovy běžné pojmy a postuláty byly považovány za skutečně pravdivé), máme zde strategii pro pochopení vesmíru. Protože někteří autoři dávají Keplerovi přívlastek iracionální, je třeba poznamenat, že tato poměrně nadějná epistemologie je skutečně velmi vzdálená mystickému přesvědčení, že věcem lze porozumět pouze nepřesným způsobem, který se opírá o poznatky nepodléhající rozumu. Kepler skutečně opakovaně děkuje Bohu za to, že mu daroval vhledy, ale tyto vhledy jsou prezentovány jako racionální.
Univerzitní vzdělání
V této době bylo obvyklé, že všichni studenti na univerzitě navštěvovali kurzy „matematiky“. V zásadě to zahrnovalo čtyři matematické vědy: aritmetiku, geometrii, astronomii a hudbu. Zdá se však, že to, co se vyučovalo, záviselo na konkrétní univerzitě. V Tübingenu Keplera učil astronomii jeden z předních astronomů té doby Michael Mästlin (1550-1631). V učebních osnovách se samozřejmě vyučovala geocentrická astronomie, tj. současná verze Ptolemaiovské soustavy, v níž se všech sedm planet – Měsíc, Merkur, Venuše, Slunce, Mars, Jupiter a Saturn – pohybovalo kolem Země a jejich polohy vůči stálicím se vypočítávaly kombinací kruhových pohybů. Tento systém víceméně odpovídal současným (aristotelským) představám o fyzice, i když se vyskytly určité potíže, například zda lze považovat za „rovnoměrný“ (a tedy přijatelný jako zjevně věčný) kruhový pohyb, který není rovnoměrný kolem vlastního středu, ale kolem jiného bodu (nazývaného „ekvant“). Zdá se však, že astronomové (kteří sami sebe považovali za „matematiky“) se vcelku spokojili s výpočty poloh planet a nechali na přírodních filozofech, aby se starali o to, zda matematické modely odpovídají fyzikálním mechanismům. Kepler tento postoj nezastával. Jeho nejstarší publikovaná práce (1596) navrhuje uvažovat o skutečných drahách planet, nikoli o kružnicích používaných k jejich konstrukci.
V Tübingenu Kepler studoval nejen matematiku, ale také řečtinu a hebrejštinu (obojí nezbytné pro čtení Písma v původních jazycích). Výuka probíhala v latině. Na konci prvního ročníku měl Kepler ze všeho kromě matematiky jedničky. Pravděpodobně se mu Mästlin snažil naznačit, že má na víc, protože Kepler byl ve skutečnosti jedním z vybraných žáků, které si vybral pro výuku pokročilejší astronomie tím, že je seznámil s novým, heliocentrickým kosmologickým systémem Koperníka. Právě od Mästlina se Kepler dozvěděl, že předmluva ke knize O revolucích, vysvětlující, že se jedná „pouze o matematiku“, není od Koperníka. Zdá se, že Kepler téměř okamžitě přijal, že Koperníkova soustava je fyzikálně pravdivá; o důvodech, proč ji přijal, bude pojednáno v souvislosti s jeho prvním kosmologickým modelem (viz níže).
Zdá se, že již za Keplerových studentských let existovaly náznaky, že jeho náboženské přesvědčení nebylo zcela v souladu s ortodoxním luteránstvím, které bylo aktuální v Tübingen a formulované v Confessio Augustana Ⓣ. Keplerovy problémy s touto protestantskou ortodoxií se týkaly údajného vztahu mezi hmotou a „duchem“ (nehmotnou entitou) v učení o eucharistii. To souvisí s Keplerovou astronomií do té míry, že zřejmě narazil na poněkud podobné intelektuální potíže při vysvětlování toho, jak může „síla“ ze Slunce působit na planety. Kepler ve svých spisech rád klade své názory na hranu – což se historikům velmi hodí. Ve skutečném životě se zdá být pravděpodobné, že podobný sklon k otevřenosti vedl úřady v Tübingen k oprávněným pochybnostem o jeho náboženské ortodoxnosti. Ty mohou vysvětlovat, proč Mästlin přesvědčil Keplera, aby se vzdal plánů na svěcení a místo toho přijal místo učitele matematiky ve Štýrském Hradci. V následujících letech se náboženská nesnášenlivost vyostřila. V roce 1612 byl Kepler exkomunikován. To mu způsobilo mnoho bolesti, ale navzdory svému (do té doby) poměrně vysokému společenskému postavení císařského matematika se mu nikdy nepodařilo dosáhnout zrušení zákazu.
Keplerův první kosmologický model (1596)
Místo sedmi planet ve standardní geocentrické astronomii jich Koperníkova soustava měla pouze šest, přičemž Měsíc se stal tělesem astronomii dosud neznámého druhu, které Kepler později nazval „satelitem“ (tento název vymyslel v roce 1610 pro měsíce, o nichž Galileo zjistil, že obíhají kolem Jupitera, což doslova znamená „doprovod“). Proč šest planet?
V geocentrické astronomii navíc neexistoval způsob, jak pomocí pozorování zjistit relativní velikosti planetárních těles; jednoduše se předpokládalo, že se dotýkají. Zdálo se, že to nevyžaduje žádné vysvětlení, protože to dobře zapadalo do přesvědčení přírodních filosofů, že celá soustava je natočena od pohybu nejvzdálenější sféry, jedné (nebo možná dvou) za sférou „stálých“ hvězd (těch, jejichž vzor tvoří souhvězdí), za sférou Saturnu. V Koperníkově soustavě umožňovala skutečnost, že roční složka pohybu každé planety byla odrazem ročního pohybu Země, využít pozorování k výpočtu velikosti dráhy každé planety a ukázalo se, že mezi planetami jsou obrovské mezery. Proč právě tyto mezery?“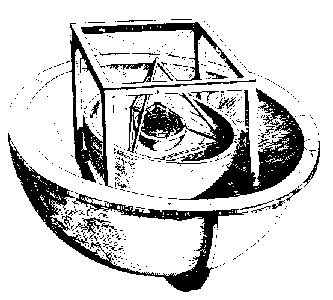
Keplerova odpověď na tyto otázky, popsaná v jeho Mysterium cosmographicum Ⓣ, Tübingen, 1596, vypadá pro čtenáře dvacátého století bizarně (viz obrázek vpravo). Navrhl, že kdyby byla nakreslena koule, která by se dotýkala vnitřní strany dráhy Saturnu, a do této koule by byla vepsána krychle, pak by koule vepsaná do této krychle byla koulí obepínající dráhu Jupiteru. Kdyby se pak do koule vepsané do dráhy Jupiteru nakreslil pravidelný čtyřstěn, byla by inspirací čtyřstěnu koule obíhající dráhu Marsu, a tak dále směrem dovnitř, čímž by se mezi Mars a Zemi vepsal pravidelný dodekaedr, mezi Zemi a Venuši pravidelný ikosaedr a mezi Venuši a Merkur pravidelný oktaedr. To dokonale vysvětluje počet planet: existuje pouze pět konvexních pravidelných těles (jak je dokázáno v Euklidových Elementech , kniha 13). Rovněž přesvědčivě odpovídá velikostem drah, jak je odvodil Koperník, přičemž největší chyba je menší než 10 % (což je na kosmologický model i v dnešní době velkolepě dobré). Kepler se nevyjadřoval v procentech chyb a jeho model je ve skutečnosti prvním matematickým kosmologickým modelem, ale je snadné pochopit, proč věřil, že pozorovací důkazy podporují jeho teorii.
Kepler považoval svou kosmologickou teorii za důkaz pro Koperníkovu teorii. Před předložením své vlastní teorie uvedl argumenty, které měly prokázat věrohodnost samotné Koperníkovy teorie. Kepler tvrdil, že její výhody oproti geocentrické teorii spočívají v její větší vysvětlující síle. Koperníkova teorie například dokáže vysvětlit, proč Venuše a Merkur nejsou nikdy vidět příliš daleko od Slunce (leží mezi Zemí a Sluncem), zatímco v geocentrické teorii pro tuto skutečnost neexistuje žádné vysvětlení. Kepler uvádí devět takových otázek v první kapitole Mysterium cosmographicum Ⓣ.
Kepler tuto práci provedl v době, kdy vyučoval ve Štýrském Hradci, ale knihu spatřil tiskem v Tübingen Mästlin. Shoda s hodnotami odvozenými z pozorování nebyla přesná a Kepler doufal, že lepší pozorování tuto shodu zlepší, a proto poslal výtisk Mysterium cosmographicum jednomu z nejvýznamnějších pozorovacích astronomů té doby, Tycho Brahemu (1546-1601). Tycho, který tehdy působil v Praze (tehdejším hlavním městě Svaté říše římské), ve skutečnosti již dříve napsal Mästlinovi, že hledá matematického asistenta. Kepler tuto práci dostal.
„Válka s Marsem“
Přirozeně, že Tychonovy priority nebyly stejné jako Keplerovy a Kepler se brzy ocitl v práci na neřešitelném problému oběžné dráhy Marsu . V práci na něm pokračoval i poté, co Tycho zemřel (v roce 1601) a Kepler ho vystřídal ve funkci císařského matematika. Oběžné dráhy se tradičně skládaly z kružnic a k určení relativních poloměrů a poloh kružnic bylo zapotřebí poměrně málo pozorovacích hodnot. Tycho provedl obrovské množství pozorování a Kepler se rozhodl je co nejlépe využít. V podstatě měl k dispozici tolik pozorování, že jakmile sestrojil možnou dráhu, mohl ji porovnávat s dalšími pozorováními, dokud nebylo dosaženo uspokojivé shody. Kepler dospěl k závěru, že dráha Marsu je elipsa se Sluncem v jednom z ohnisek (výsledek, který se po rozšíření na všechny planety dnes nazývá „první Keplerův zákon“) a že přímka spojující planetu se Sluncem vymetá ve stejných časech stejné plochy, jak planeta opisuje svou dráhu („druhý Keplerův zákon“), tj. plocha se používá jako míra času. Poté, co byla tato práce publikována v časopise Astronomia nova, … Ⓣ, Heidelberg, 1609, Kepler našel dráhy i pro ostatní planety, čímž zjistil, že oba zákony platí i pro ně. Oba zákony se vztahují k pohybu planety vůči Slunci; Keplerův kopernikanismus byl pro jeho úvahy a dedukce klíčový.
Samotný proces výpočtu pro Mars byl nesmírně pracný – dochovalo se téměř tisíc listů aritmetiky – a Kepler sám tuto práci označuje za „mou válku s Marsem“, ale výsledkem byla dráha, která se shoduje s moderními výsledky tak přesně, že při srovnání je třeba zohlednit sekulární změny dráhy od Keplerovy doby.
Observační chyba
Pro Keplerovu metodu porovnávání možných oběžných drah s pozorováními bylo klíčové, aby měl představu o tom, co by mělo být přijato jako přiměřená shoda. Z toho vyplývá první explicitní použití pojmu pozorovací chyba. Za tento pojem Kepler možná alespoň částečně vděčil Tychonovi, který podrobně kontroloval výkon svých přístrojů (viz Braheho životopis).
Optika a nová hvězda z roku 1604
Práce o Marsu byla v podstatě dokončena v roce 1605, ale došlo ke zpoždění při vydávání knihy. Mezitím Kepler v reakci na obavy z rozdílného zdánlivého průměru Měsíce při přímém pozorování a při pozorování pomocí camery obscury pracoval na optice a přišel s první správnou matematickou teorií camery obscury a prvním správným vysvětlením fungování lidského oka s obráceným obrazem vytvořeným na sítnici. Tyto výsledky byly publikovány ve spise Ad Vitellionem paralipomena, quibus astronomiae pars optica traditur Ⓣ, Frankfurt, 1604. Psal také o nové hvězdě z roku 1604, dnes obvykle nazývané „Keplerova supernova“, přičemž odmítl četná vysvětlení a na jednom místě poznamenal, že tato hvězda by samozřejmě mohla být jen zvláštním výtvorem, „ale než k tomu dojdeme, myslím, že bychom měli vyzkoušet všechno ostatní.“ De stella nova Ⓣ, Praha, 1606, kapitola 22, KGW 1, s. 257, řádek 23.
Po Galileově využití dalekohledu při objevu Jupiterových měsíců, publikovaném v jeho Hvězdném poselstvu (Benátky, 1610), na které Kepler napsal nadšenou odpověď (1610), napsal Kepler studii o vlastnostech čoček (první takové dílo o optice), v níž představil novou konstrukci dalekohledu, využívajícího dvě konvexní čočky (Dioptrice, Praha, 1611). Tato konstrukce, v níž je výsledný obraz převrácený, byla tak úspěšná, že se jí dnes obvykle neříká Keplerův dalekohled, ale prostě astronomický dalekohled.
Odchod z Prahy do Lince
Keplerova léta v Praze byla relativně klidná a vědecky mimořádně produktivní. Dokonce se zdá, že i když se mu nedařilo, nikdy nedovolil, aby mu vnější okolnosti zabránily pokračovat v práci. Velmi špatně se začalo dařit koncem roku 1611. Nejprve mu zemřel sedmiletý syn. Kepler napsal svému příteli, že tuto smrt nesl obzvlášť těžce, protože dítě mu v tomto věku velmi připomínalo jeho samotného. Poté zemřela Keplerova manželka. Tehdy byl císař Rudolf, jehož zdraví se zhoršovalo, nucen abdikovat ve prospěch svého bratra Matyáše, který byl stejně jako Rudolf katolík, ale (na rozdíl od Rudolfa) nevěřil v toleranci vůči protestantům. Kepler musel opustit Prahu. Před odjezdem nechal přenést tělo své ženy do hrobu syna a napsal pro ně latinský epitaf. Se zbývajícími dětmi se přestěhoval do Lince (dnes v Rakousku).
Sňatek a sudy s vínem
Kepler se zřejmě oženil se svou první ženou Barborou z lásky (i když sňatek byl sjednán přes zprostředkovatele). Druhý sňatek v roce 1613 byl otázkou praktické nutnosti; potřeboval někoho, kdo by se postaral o děti. Keplerova nová žena Susanna prošla rychlokurzem Keplerovy povahy: v dedikačním dopise k výsledné knize vysvětluje, že si při svatebních oslavách všiml, že objemy sudů s vínem se odhadují pomocí tyče zasunuté šikmo skrz otvor v sudu, a začal se zajímat, jak to může fungovat. Výsledkem byla studie o objemech rotačních těles Nova stereometria doliorum … Ⓣ, Linz, 1615, v níž Kepler, vycházeje z Archimédova díla, použil rozlišení na „nedělitelné“. Tuto metodu později rozvinul Bonaventura Cavalieri (asi 1598-1647) a patří k předkům infinitezimálního počtu.
Harmonie světa
Keplerovým hlavním úkolem jako císařského matematika bylo napsat astronomické tabulky na základě Tychonových pozorování, ale ve skutečnosti chtěl napsat Harmonii světa, plánovanou od roku 1599 jako rozvinutí jeho Tajemství kosmu. Toto druhé dílo o kosmologii (Harmonices mundi libri V Ⓣ, Linz, 1619) představuje propracovanější matematický model než předchozí, i když mnohostěny v něm zůstaly. Matematika v tomto díle zahrnuje první systematické pojednání o tesselacích, důkaz, že existuje pouze třináct konvexních rovnoměrných mnohostěnů (Archimédova tělesa), a první popis dvou nekonvexních pravidelných mnohostěnů (vše ve 2. knize). Harmonie světa obsahuje také to, co je dnes známo jako „třetí Keplerův zákon“, že pro libovolné dvě planety bude poměr čtverců jejich period stejný jako poměr krychlí středních poloměrů jejich oběžných drah. Kepler od počátku hledal pravidlo, které by vztahovalo velikosti oběžných drah k periodám, ale k tomuto zákonu nevedla žádná pomalá řada kroků, jako tomu bylo u dvou předchozích. Ačkoli třetí zákon hraje důležitou roli v některých závěrečných částech tištěné verze Harmonie světa, ve skutečnosti byl objeven až v době, kdy bylo dílo v tisku. Kepler provedl úpravy na poslední chvíli. Sám vypráví příběh o konečném úspěchu:
…a chcete-li přesný časový okamžik, byla myšlenkově koncipována 8. března tohoto roku tisíc šest set osmnáct, ale nešťastným způsobem podrobena výpočtu, a proto zamítnuta jako falešná, a nakonec se vrátila 15. května a přijala novou linii útoku, burcovala temnoty mé mysli. Kombinace mé sedmnáctileté práce na Braheho pozorování a této studie, které se spolu spikly, byla tak silnou oporou, že jsem zprvu věřil, že se mi to jen zdá, a svůj závěr jsem předpokládal mezi základními premisami. Je však naprosto jisté a přesné, že „poměr mezi periodickými časy jakýchkoli dvou planet je přesně roven sesquialterate proportion of their mean distances …“
(Harmonice mundi kniha 5, kapitola 3, trans. Aiton, Duncan a Field, s. 411).
Čarodějnický proces
Když Kepler pracoval na své Harmonii světa, byla jeho matka obviněna z čarodějnictví. Požádal o pomoc právnickou fakultu v Tübingenu. Katharina Keplerová byla nakonec propuštěna, přinejmenším částečně v důsledku technických námitek vyplývajících z toho, že úřady nedodržely správné právní postupy při použití mučení. Z dochovaných dokumentů mrazí. Keplerová však pokračovala v práci. V kočáře na cestě do Württemberska na obhajobu své matky četl dílo Vincenza Galileiho (asi 1520 – 1591, Galileův otec) o hudební teorii, na které jsou v Harmonii světa četné odkazy.
Astronomické tabulky
Výpočet tabulek, běžná činnost astronoma, vždy zahrnoval těžkou aritmetiku. Kepler byl proto potěšen, když v roce 1616 narazil na Napierovu práci o logaritmech (vydanou v roce 1614). Mästlin mu však okamžitě sdělil, že jednak není vhodné, aby se seriózní matematik radoval z pouhé pomůcky k výpočtu, a jednak že není moudré logaritmům důvěřovat, protože nikdo nechápe, jak fungují. (Podobné poznámky zazněly počátkem šedesátých let o počítačích.) Keplerovou odpovědí na druhou námitku bylo zveřejnění důkazu, jak logaritmy fungují, založeného na bezvadně seriózním zdroji: Euklidových prvků, kniha 5. Kepler vypočítal tabulky osmimístných logaritmů, které byly publikovány spolu s Rudolfínskými tabulkami (Ulm, 1628). Astronomické tabulky využívaly nejen Tychova pozorování, ale také první dva Keplerovy zákony. Všechny astronomické tabulky, které využívaly nová pozorování, byly prvních několik let po zveřejnění přesné. Pozoruhodné na Rudolfínských tabulkách bylo, že se ukázaly být přesné po celá desetiletí. A jak léta přibývala, byla trvalá přesnost tabulek přirozeně považována za argument pro správnost Keplerových zákonů, a tedy i pro správnost heliocentrické astronomie. Keplerovo plnění nudného úředního úkolu císařského matematika vedlo ke splnění jeho nejtajnějšího přání – pomoci zavést kopernikanismus.
Wallenstein
V době vydání Rudolfových tabulek už Kepler ve skutečnosti nepracoval pro císaře (z Lince odešel v roce 1626), ale pro Albrechta z Valdštejna (1583-1632), jednoho z mála úspěšných vojevůdců ve třicetileté válce (1618-1648).
Wallenstein, stejně jako císař Rudolf, očekával, že mu Kepler poskytne rady založené na astrologii. Kepler ho samozřejmě musel poslechnout, ale opakovaně zdůrazňoval, že nevěří v možnost přesných předpovědí. Stejně jako většina lidí té doby i Kepler uznával princip astrologie, že nebeská tělesa mohou ovlivňovat dění na Zemi (nejzřetelnějším příkladem je Slunce způsobující roční období a Měsíc příliv a odliv), ale jako kopernikán nevěřil ve fyzikální realitu souhvězdí. Jeho astrologie byla založena pouze na úhlech mezi polohami nebeských těles („astrologické aspekty“). Vyjadřuje naprosté pohrdání komplikovanými systémy konvenční astrologie.
Smrt
Kepler zemřel v Regensburgu po krátké nemoci. Ve městě se zdržoval na cestě za penězi, které mu náležely v souvislosti s Rudolfínskými tabulkami. Byl pohřben v místním kostele, ten však byl v průběhu třicetileté války zničen a z hrobky nezbylo nic.
Historiografická poznámka
V Keplerově vědecké činnosti se někdy hodně poukazuje na údajně neracionální prvky. Věřící astrologové často tvrdí, že jeho dílo poskytuje vědecky úctyhodný předstupeň jejich vlastnímu dílu. Zesnulý Arthur Koestler ve svém vlivném díle Náměsíčníci učinil z Keplerova boje s Marsem argument pro inherentní iracionalitu moderní vědy. Tichých následovníků těchto dvou přesvědčení bylo mnoho. Obě však vycházejí z velmi dílčího čtení Keplerova díla. Zejména Koestler zřejmě neměl dostatečné matematické znalosti, aby Keplerovým postupům porozuměl. Bližší studium ukazuje, že Koestler se ve svém hodnocení jednoduše mýlil.
Skutečně důležitým neracionálním prvkem v Keplerově díle je jeho křesťanství. Keplerovo rozsáhlé a úspěšné používání matematiky činí jeho dílo „moderním“, ale ve skutečnosti máme co do činění s křesťanským přírodním filosofem, pro něhož pochopení podstaty vesmíru zahrnovalo i pochopení podstaty jeho Stvořitele.