V níže uvedené tabulce frekvencí najdete A = 440 Hz, dále
A# = 466,16 Hz,
B = 493,88 Hz,
C = 523,25 Hz atd.
Také můžete najít střední C: 261. V tabulce frekvencí je uvedeno, že A = 440 Hz.63 Hz.
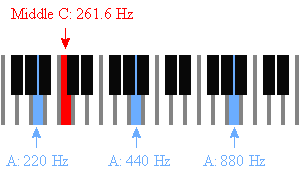
Tabulka hudebních frekvencí
Note
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
Frequency
130.82
138.59
146.83
155.56
164.81
174.61
185
196
207.65
220
233.08
246.94
Nota
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
Frekvence
261.63
277.18
293.66
311.13
329.63
349.23
369.99
392
415.3
440
466.16
493.88
Nota
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
Frekvence
523.25
554.37
587.33
622.25
659.26
698.46
739.99
783.99
830.61
880
932.33
987.77
Nota
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
C
Frekvence
1046.5
1108.73
1174.66
1244.51
1318.51
1396.91
1479.98
1567.98
1661.22
1760
1864.66
1975.53
2093.00
Ty se zjistí pomocí
frekvence `= 440×2^(n“/“12)`
pro `n = -21, -19, …., 27`
Kde se tento vzorec vzal?
Tato úloha mi připomněla Složené úročení, se kterým jsme se setkali dříve v Matematice peněz. Frekvence se musí zdvojnásobit každých `12` tónů (protože v každé oktávě je `7` bílých tónů a `5` černých tónů.)
Tady je graf tohoto vztahu:
frekvence `= 440×2^(n“/“12)`
Jedná se o exponenciální křivku, se kterou jsme se již dříve setkali v Grafech exponenciálních funkcí.
Rovnoměrné temperované ladění
Zajímavý problém, se kterým se výrobci hudebních nástrojů potýkají již stovky let. Abychom získali „dokonalou pětku“ (interval mezi A a výše uvedeným E), musíme zahrát tón, který má `1,5` násobek frekvence A.
Na houslích (nebo na viole či jiném bezpražcovém strunném nástroji) je to možné a můžeme zahrát krásné, dokonalé E s frekvencí `440 × 1,5 = 660\“Hz“`. Všimněte si však (podle výše uvedené tabulky frekvencí), že klavír hrající stejný tón zahraje E `= 659,26\“Hz“` .
Přibližně před 400 lety byly klávesové nástroje (obvykle cembala a varhany) naladěny pro určitou skupinu kláves, takže všechny nástroje, zejména smyčcové, zněly v těchto klávesách „správně“. Cembalo znělo v těchto tóninách skvěle, ale v jiných nesouvisejících tóninách (například v béčku) dost hrozně.
V Bachově době se ve skutečnosti používalo několik různých systémů ladění, včetně meantone (jehož cílem bylo, aby dobře zněly durové tercie, ale nestaral se tolik o kvalitu durových kvint, což mělo za následek, že některé tóniny nebyly použitelné) a Werckmeisterova ladění z roku 1691, které skladatelům umožňovalo vytvářet hudbu v libovolné tónině (což mělo za následek, že různé tóniny měly různou zvukovou kvalitu).
Na počátku 20. století bylo rozhodnuto naladit klávesy tak, aby byly noty rovnoměrně rozloženy (jako frekvence uvedené ve výše uvedené tabulce). Tomuto ladění se říká rovnoměrné temperované ladění. Takové ladění bylo známo již v Bachově době, ale bylo zavrženo, protože bylo považováno za příliš „nevýrazné“ (všechny klávesy mají stejnou kvalitu tónu) a neexistovaly nástroje pro měření frekvence, které by umožnily přesné ladění.
Naneštěstí rovnoměrné temperované ladění znamená, že všechny smyčcové nástroje musí počítat s mírnými rozdíly v ladění mezi jednotlivými nástroji, pokud se jedná i o klávesové nástroje. Struny jsou z tohoto důvodu obvykle nejšťastnější, když hrají pouze s jinými strunami.
nahoru
Vyhledávání IntMath
Online řešitel trigonometrie
Tento řešitel trigonometrie dokáže řešit širokou škálu matematických úloh.
Přejít na: Řešitel trigonometrie online
.