I tabellen över frekvenser nedan hittar du A = 440 Hz, och sedan
A# = 466,16 Hz,
B = 493,88 Hz,
C = 523,25 Hz, osv.
Det finns även ett mellanslag C: 261.63 Hz.
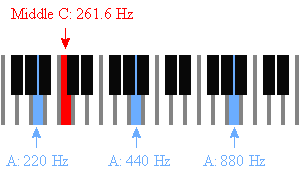
Tabell över musikaliska frekvenser
Note
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
Frequency
130.82
138.59
146.83
155.56
164.81
174.61
185
196
207.65
220
233.08
246.94
Note
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
Frekvens
261.63
277.18
293.66
311.13
329.63
349.23
369.99
392
415.3
440
466.16
493.88
Note
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
Frekvens
523.25
554.37
587.33
622.25
659.26
698.46
739.99
783.99
830.61
880
932.33
987.77
Note
C
C#
D
D#
E
F
F#
G
G#
A
A#
A#
B
C
Frekvens
1046.5
1108.73
1174.66
1244.51
1318.51
1396.91
1479.98
1567.98
1661.22
1760
1864.66
1975.53
2093.00
Dessa hittas med hjälp av
frekvens `= 440×2^(n”/”12)`
för `n = -21, -19, …., 27`
Varifrån kommer denna formel?
Detta problem påminde mig om den sammansatta räntan som vi träffade tidigare i penningmatematik. Frekvensen måste fördubblas var 12:e ton (eftersom det finns 7 vita toner och 5 svarta toner i varje oktav).
Här är en graf för detta förhållande:
Frekvens `= 440×2^(n”/”12)`
Det här är en exponentiell kurva som vi tidigare har lärt oss om i Grafer för exponentiella funktioner.
Jämntempererad stämning
Ett intressant problem har musikinstrumenttillverkare ställts inför i hundratals år. För att få en ”perfekt 5:e” (t.ex. intervallet mellan A och E ovanför) måste vi spela en ton som har `1,5` gånger frekvensen av A.
På en fiol (eller viola eller något annat fretless stränginstrument) är detta möjligt, och vi kan spela ett vackert, perfekt E på `440 × 1,5 = 660\ ”Hz”`. Men notera (från frekvenstabellen ovan) att ett piano som spelar samma ton kommer att spela E `= 659,26\ ”Hz”` .
För omkring 400 år sedan stämdes klaviaturer (vanligen cembalos och orglar) för en viss grupp tangenter, så att alla instrument, särskilt strängar, lät ”rätt” i dessa tangenter. Cembalon lät bra i dessa tonarter, men ganska hemskt i andra tonarter som inte hade något samband med dem (till exempel B-dur).
Det fanns faktiskt flera olika stämningssystem som användes under Bachs tid, bland annat meantone (som syftade till att få stora 3:or att låta bra, men som inte brydde sig lika mycket om kvaliteten på stora 5:or, med följden att vissa tonarter inte kunde användas) och Werckmeisters stämning från 1691, som gjorde det möjligt för kompositörer att skapa musik i vilken tonart som helst (med följden att de olika tonarterna hade olika klangkvalitet).
I början av 1900-talet bestämde man sig för att stämma tangentbord så att tonerna var jämnt fördelade (som de frekvenser som anges i tabellen ovan). Detta kallas jämntempererad stämning. En sådan stämning var känd på Bachs tid, men förkastades eftersom den ansågs alltför ”intetsägande” (alla tangenter har samma tonkvalitet) och det inte fanns några frekvensmätningsverktyg som skulle ha möjliggjort exakta stämningar.
Olyckligtvis innebär den jämntempererade stämningen att alla stränginstrument måste ta hänsyn till de små skillnaderna i stämningar mellan instrumenten när även klaviaturer är inblandade. Strängar är vanligtvis lyckligast när de bara spelar med andra strängar av denna anledning.
top
Sök IntMath
Online trigonometri-lösare
Den här trigonometri-lösaren kan lösa ett brett spektrum av matematiska problem.
Gå till: Trigonometrilösare online