En ekvation i form av lutning och intercept skrivs som
$$$y=mx+b$$
Varvid m är linjens lutning och b är y-interceptet. Du kan använda denna ekvation för att skriva en ekvation om du känner till lutningen och y-interceptet.
Exempel
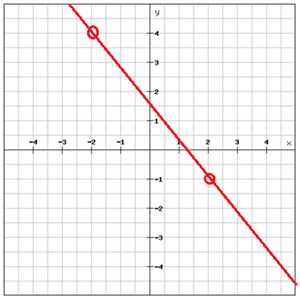
Finn ekvationen för linjen
Välj två punkter som ligger på linjen
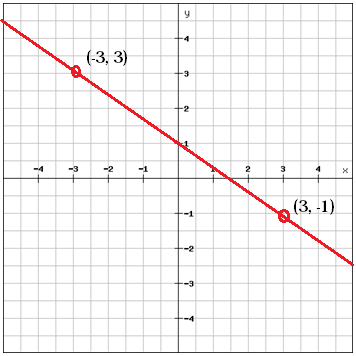
Beräkna lutningen mellan de två punkterna
$$$m=\frac{y_{2}\, -y_{1}}{x_{2}\, -x_{1}}}=\frac{\left (-1 \right )-3}{3-\left ( -3 \right )}=\frac{-4}{6}=\frac{-2}{3}$$$
Vi kan hitta b-värdet, y-interceptet, genom att titta på grafen
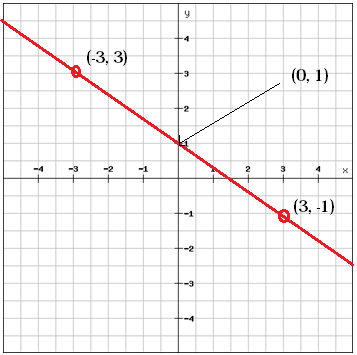
b = 1
Vi har fått ett värde för m och ett värde för b. Detta ger oss den linjära funktionen
$$$y=-\frac{2}{3}x+1$$$
I många fall är värdet på b inte lika lätt att utläsa. I dessa fall, eller om du är osäker på om linjen faktiskt korsar y-axeln i just denna punkt kan du beräkna b genom att lösa ekvationen för b och sedan ersätta x och y med en av dina två punkter.
Vi kan använda exemplet ovan för att illustrera detta. Vi har de två punkterna (-3, 3) och (3, -1). Från dessa två punkter beräknade vi lutningen
$$$m=-\frac{2}{3}$$$
Detta ger oss ekvationen
$$y=-\frac{2}{3}x+b$$$
Från detta kan vi lösa ekvationen för b
$$b=y+\frac{2}{3}x$$
Och om vi sätter in värdena från vår första punkt (-3, 3) får vi
$$b=3+\frac{2}{3}\cdot \left ( -3 \right )=3+\left ( -2 \right )=1$$$
Om vi sätter in detta värde för b i ekvationen får vi
$$y=-\frac{2}{3}x+1$$$
vilket är samma ekvation som vi fick när vi läste y-interceptet från grafen.
För att sammanfatta hur man skriver en linjär ekvation med hjälp av lutningsinterceptionsformen ska man
- Identifiera lutningen, m. Detta kan göras genom att beräkna lutningen mellan två kända punkter på linjen med hjälp av lutningsformeln.
- Hitta y-interceptet. Detta kan göras genom att ersätta lutningen och koordinaterna för en punkt (x, y) på linjen i lutningsinterceptformeln och sedan lösa b.
När du har fått fram både m och b kan du bara sätta in dem i ekvationen på sina respektive positioner.
Videolektion
Finn ekvationen till grafen