Selection Sort – Algoritm, källkod, tidskomplexitet

Denna artikel är en del av serien ”Sorteringsalgoritmer: Den…

• beskriver hur Selection Sort fungerar,
• inkluderar Java-källkoden för Selection Sort,
• visar hur man kan härleda dess tidskomplexitet (utan komplicerad matematik)
• och kontrollerar om prestandan hos Java-implementationen stämmer överens med det förväntade körtidsbeteendet.

Källkoden för hela artikelserien finns i mitt GitHub-förråd.

Exempel: Sortering av spelkort

Sortering av spelkort i handen är det klassiska exemplet på Insertion Sort.

Selection Sort kan också illustreras med spelkort. Jag känner ingen som plockar sina kort på detta sätt, men som exempel fungerar det ganska bra 😉

Först lägger du alla dina kort med framsidan uppåt på bordet framför dig. Du letar efter det minsta kortet och tar det till vänster om din hand. Sedan letar du efter nästa större kort och lägger det till höger om det minsta kortet, och så vidare tills du slutligen tar det största kortet längst till höger.

Skillnad mot insättningssortering

Med insättningssortering tog vi nästa osorterade kort och satte in det på rätt plats i de sorterade korten.

Selekteringssortering fungerar ungefär tvärtom: Vi väljer det minsta kortet från de osorterade korten och lägger sedan – ett efter ett – till det i de redan sorterade korten.

Algoritm för urvalssortering

Algoritmen kan förklaras enklast med ett exempel. I följande steg visar jag hur man sorterar matrisen med Selection Sort:

Steg 1

Vi delar upp matrisen i en vänster, sorterad del och en höger, osorterad del. Den sorterade delen är tom i början:

Steg 2

Vi söker efter det minsta elementet i den högra, osorterade delen. För att göra detta kommer vi först ihåg det första elementet, som är 6. Vi går till nästa fält, där vi hittar ett ännu mindre element i 2. Vi går över resten av matrisen och letar efter ett ännu mindre element. Eftersom vi inte kan hitta något håller vi oss till 2. Vi placerar det på rätt plats genom att byta ut det med elementet på första plats. Sedan flyttar vi gränsen mellan arraydelarna ett fält till höger:

Steg 3

Vi söker återigen i den högra, osorterade delen efter det minsta elementet. Den här gången är det 3:an; vi byter ut den mot elementet i andra positionen:

Steg 4

Vi söker återigen efter det minsta elementet i den högra delen. Det är 4, som redan befinner sig på rätt plats. Så det behövs ingen bytesoperation i detta steg, och vi flyttar bara sektionsgränsen:

Steg 5

Som det minsta elementet hittar vi 6. Vi byter ut det mot elementet i början av den högra delen, 9:

Steg 6

Av de återstående två elementen är 7 det minsta. Vi byter ut den mot 9:

Algoritmen avslutad

Det sista elementet är automatiskt det största och därför i rätt position. Algoritmen är avslutad och elementen är sorterade:

Selektionssortering Java-källkod

I det här avsnittet hittar du en enkel Java-implementering av Selektionssortering.

Den yttre slingan itererar över de element som ska sorteras, och den avslutas efter det näst sista elementet. När detta element sorteras sorteras det sista elementet automatiskt också. Loopvariabeln i pekar alltid på det första elementet i den högra, osorterade delen.

I varje loopcykel antas det första elementet i den högra delen inledningsvis vara det minsta elementet min; dess position lagras i minPos.

Den inre slingan itererar sedan från det andra elementet i den högra delen till dess slut och omfördelar min och minPos varje gång ett ännu mindre element hittas.

När den inre slingan är avslutad byts elementen på positionerna i (början av den högra delen) och minPos ut (om de inte är samma element).

public class SelectionSort { public static void sort(int elements) { int length = elements.length; for (int i = 0; i < length - 1; i++) { // Search the smallest element in the remaining array int minPos = i; int min = elements; for (int j = i + 1; j < length; j++) { if (elements < min) { minPos = j; min = elements; } } // Swap min with element at pos i if (minPos != i) { elements = elements; elements = min; } } }}

Koden som visas skiljer sig från SelectionSort-klassen i GitHub-förrådet genom att den implementerar gränssnittet SortAlgorithm för att vara lätt utbytbar inom testramverket.

Selektionssorteringens tidskomplexitet

Vi betecknar med n antalet element, i vårt exempel är n = 6.

De två inbäddade slingorna är en indikation på att vi har att göra med en tidskomplexitet* på O(n²). Detta kommer att vara fallet om båda slingorna itererar till ett värde som ökar linjärt med n.

Det är uppenbarligen fallet med den yttre slingan: den räknar upp till n-1.

Hur är det med den inre slingan?

Se på följande illustration:

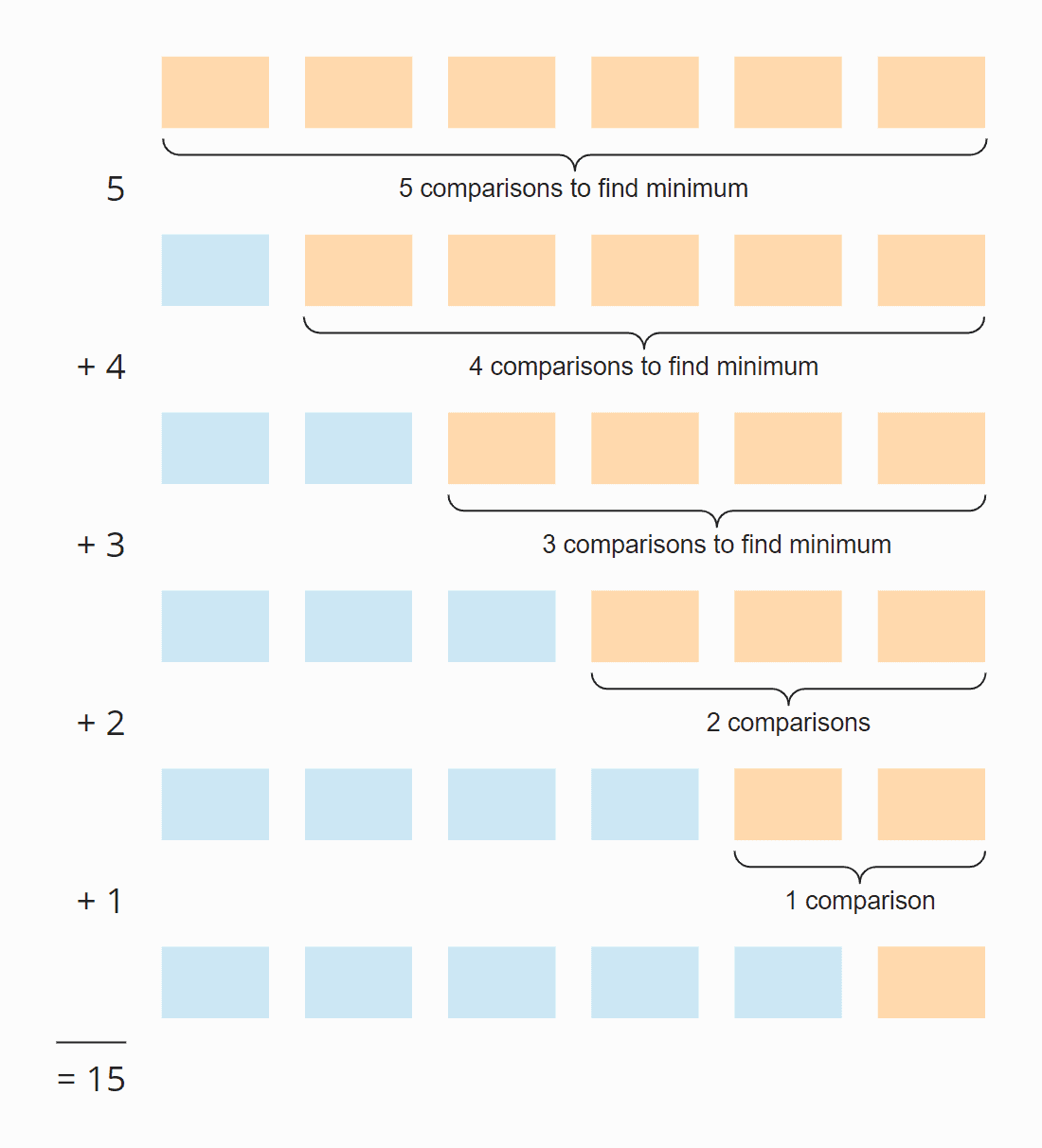
I varje steg är antalet jämförelser ett mindre än antalet osorterade element. Sammanlagt görs 15 jämförelser – oavsett om matrisen initialt är sorterad eller inte.

Detta kan också beräknas på följande sätt:

Sex element gånger fem steg; delat med två, eftersom i genomsnitt över alla steg är hälften av elementen fortfarande osorterade:

6 × 5 × ½ = 30 × ½ = 15

Om vi ersätter 6 med n får vi

n × (n – 1) × ½

När det multipliceras blir det:

½ n² – ½ n

Den högsta potensen av n i denna term är n². Tidskomplexiteten för att söka det minsta elementet är därför O(n²) – även kallad ”kvadratisk tid”.

Låt oss nu titta på bytet av elementen. I varje steg (utom det sista) byts antingen ett element eller inget, beroende på om det minsta elementet redan befinner sig på rätt plats eller inte. Vi har alltså sammanlagt högst n-1 bytesoperationer, dvs. en tidskomplexitet på O(n) – även kallad ”linjär tid”.

För den totala komplexiteten spelar endast den högsta komplexitetsklassen någon roll, därför:

Den genomsnittliga, bästa och sämsta tidskomplexiteten för Selection Sort är: O(n²)

* Termerna ”tidskomplexitet” och ”O-notation” förklaras i den här artikeln med hjälp av exempel och diagram.

Runtime of the Java Selection Sort Example

Genom teori! Jag har skrivit ett testprogram som mäter körtiden för Selection Sort (och alla andra sorteringsalgoritmer som behandlas i den här serien) enligt följande:

• Antalet element som ska sorteras fördubblas efter varje iteration från ursprungligen 1 024 element upp till 536 870 912 (= 229) element. En matris som är dubbelt så stor kan inte skapas i Java.
• Om ett test tar längre tid än 20 sekunder utökas inte matrisen ytterligare.
• Alla tester körs med osorterade samt stigande och fallande försorterade element.
• Vi låter HotSpot-kompilatorn optimera koden med två uppvärmningsrundor. Därefter upprepas testerna tills processen avbryts.

Efter varje iteration skriver programmet ut medianen av alla tidigare mätresultat.

Här är resultatet för Selection Sort efter 50 iterationer (för tydlighetens skull är detta bara ett utdrag; det fullständiga resultatet finns här):

n	unsorterat	uppstigande	nedåtgående	nedåtgående
…	…	…	…
16.384	27,9 ms	26,8 ms	65,6 ms
32.768	108,0 ms	105,4 ms	265,4 ms
65.536	434,0 ms	424,3 ms	1.052,2 ms
131.072	1.729,8 ms	1.714,1 ms	4.209,9 ms
262.144	6.913,4 ms	6.880,2 ms	16.863,7 ms
524.288	27.649,8 ms	27.568,7 ms	67.537,8 ms

Här är mätningarna återigen som ett diagram (där jag har visat ”osorterad” och ”stigande” som en kurva på grund av de nästan identiska värdena):

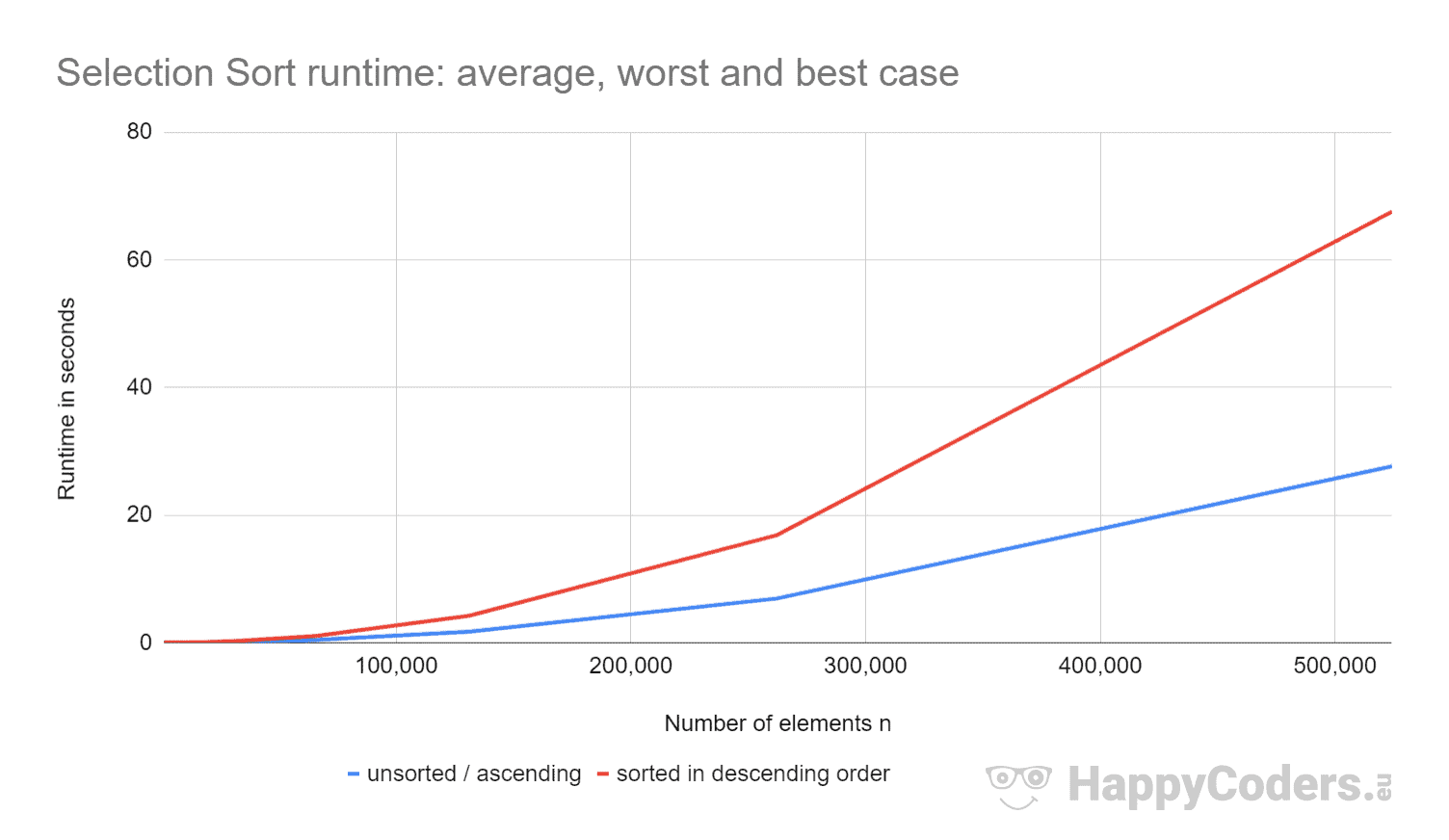
Det är bra att se att

• om antalet element fördubblas så fyrdubblas körtiden ungefär – oavsett om elementen tidigare är sorterade eller inte. Detta motsvarar den förväntade tidskomplexiteten O(n²).
• att körtiden för stigande sorterade element är något bättre än för osorterade element. Detta beror på att bytesoperationerna, som – enligt analysen ovan – har liten betydelse, inte är nödvändiga här.
• att körtiden för fallande sorterade element är betydligt sämre än för osorterade element.

Varför är det så?

Analys av den sämsta körtiden

Teoretiskt sett bör sökningen efter det minsta elementet alltid ta lika lång tid, oavsett utgångsläget. Och bytesoperationerna borde bara vara något mer för element som är sorterade i fallande ordning (för element som är sorterade i fallande ordning måste varje element bytas; för osorterade element måste nästan varje element bytas).

Med hjälp av programmet CountOperations från mitt GitHub repository kan vi se antalet olika operationer. Här är resultaten för osorterade element och element sorterade i fallande ordning, sammanfattade i en tabell:

n	Varianter	Swaps unsorterade	Swaps nedåtgående	minPos/min osorterad	minPos/min nedåtgående
…	…	…	…	…	…
512	130.816	504	256	2.866	66.047
1.024	523.776	1.017	512	6.439	263.167
2.048	2.096.128	2.042	1.024	14.727	1.050.623
4.096	8.386.560	4.084	2.048	30.758	4.198.399
8.192	33.550.336	8.181	4.096	69.378	16.785.407

Från de uppmätta värdena kan man se:

• Med element som är sorterade i fallande ordning har vi – som förväntat – lika många jämförelser som med osorterade element – det vill säga n × (n-1) / 2.
• Med osorterade element har vi – som förväntat – nästan lika många bytesoperationer som element: till exempel, med 4 096 osorterade element finns det 4 084 bytesoperationer. Dessa siffror ändras slumpmässigt från test till test.
• Med element som är sorterade i fallande ordning har vi dock bara hälften så många bytesoperationer som element! Detta beror på att vi när vi byter inte bara placerar det minsta elementet på rätt plats, utan även respektive bytespartner.

Med åtta element har vi till exempel fyra bytesoperationer. I de fyra första iterationerna har vi en vardera och i iterationerna fem till åtta ingen (trots detta fortsätter algoritmen att köras till slutet):

Fortfarande kan vi utläsa av mätningarna:

• Anledningen till att Selection Sort är så mycket långsammare med element som är sorterade i fallande ordning kan hittas i antalet tilldelningar av lokala variabler (minPos och min) när man söker efter det minsta elementet. Medan vi med 8 192 osorterade element har 69 378 av dessa tilldelningar, finns det med element sorterade i fallande ordning 16 785 407 sådana tilldelningar – det är 242 gånger så många!

Varför denna enorma skillnad?

Analys av körtiden för sökning efter det minsta elementet

För element som sorteras i fallande ordning kan storleksordningen härledas från illustrationen just ovan. Sökningen efter det minsta elementet är begränsad till triangeln av de orangefärgade och orangeblå rutorna. I den övre orangea delen blir siffrorna i varje ruta mindre, i den högra orangeblåa delen ökar siffrorna igen.

Tilldelningsoperationer äger rum i varje orange ruta och i den första av de orangeblå rutorna. Antalet tilldelningsoperationer för minPos och min är alltså bildligt talat ungefär ”en fjärdedel av kvadraten” – matematiskt och exakt är det ¼ n² + n – 1.

För osorterade element skulle vi behöva tränga mycket djupare in i saken. Det skulle inte bara gå utanför ramen för den här artikeln, utan för hela bloggen.

Därmed begränsar jag min analys till ett litet demoprogram som mäter hur många minPos/min-uppdrag det finns när man söker efter det minsta elementet i en osorterad array. Här är medelvärdena efter 100 iterationer (ett litet utdrag; de fullständiga resultaten finns här):

n	genomsnittligt antal minPos/min-uppdrag
1.024	7.08
4.096	8.61
16.385	8.94
65.536	11.81
262.144	12.22
1.048.576	14.26
4.194.304	14.71
16.777.216	16.44
67.108.864	17.92
268.435.456	20.27

Här kommer ett diagram med logaritmisk x-axel:

Diagrammet visar mycket snyggt att vi har logaritmisk tillväxt, dvs, med varje fördubbling av antalet element ökar antalet uppdrag endast med ett konstant värde. Som sagt kommer jag inte att gå djupare in på matematiska bakgrunder.

Detta är anledningen till att dessa minPos/min-uppdrag har liten betydelse i osorterade matriser.

Andra egenskaper hos Selection Sort

I de följande avsnitten kommer jag att diskutera Selection Sorts utrymmeskomplexitet, stabilitet och parallelliseringsförmåga.

Rymdkomplexitet för Selection Sort

Selection Sorts rymdkomplexitet är konstant eftersom vi inte behöver något ytterligare minnesutrymme bortsett från loopvariablerna i och j och hjälpvariablerna length, minPos och min.

Det vill säga, oavsett hur många element vi sorterar – tio eller tio miljoner – behöver vi bara dessa fem ytterligare variabler. Vi noterar konstant tid som O(1).

Stabilitet för Selection Sort

Selection Sort verkar stabil vid första anblicken: Om den osorterade delen innehåller flera element med samma nyckel ska det första av dem läggas till den sorterade delen först.

Men skenet är bedrägligt. Genom att byta ut två element i algoritmens andra delsteg kan det hända att vissa element i den osorterade delen inte längre har den ursprungliga ordningen. Detta leder i sin tur till att de inte längre förekommer i den ursprungliga ordningen i den sorterade delen.

Ett exempel kan konstrueras mycket enkelt. Anta att vi har två olika element med nyckel 2 och ett med nyckel 1, ordnade enligt följande, och sedan sorterar dem med Selection Sort:

I det första steget byts det första och sista elementet ut. Således hamnar elementet ”TWO” bakom elementet ”two” – ordningen på de båda elementen är ombytta.

I det andra steget jämför algoritmen de två bakre elementen. Båda har samma nyckel, 2. Inget element byts alltså ut.

I det tredje steget återstår endast ett element; detta anses automatiskt vara sorterat.

De två elementen med nyckeln 2 har alltså bytts ut till sin ursprungliga ordning – algoritmen är instabil.

Stabil variant av Selection Sort

Selection Sort kan göras stabil genom att inte byta ut det minsta elementet mot det första i steg två, utan genom att flytta alla element mellan det första och det minsta elementet en position åt höger och sätta in det minsta elementet i början.

Även om tidskomplexiteten förblir densamma på grund av den här ändringen kommer de extra förskjutningarna att leda till en betydande prestandaförlust, åtminstone när vi sorterar en array.

Med en länkad lista kan man klippa och klistra in det element som ska sorteras utan någon betydande prestandaförlust.

Paralleliserbarhet för selektionssortering

Vi kan inte parallellisera den yttre slingan eftersom den ändrar innehållet i arrayen i varje iteration.

Den inre slingan (sökning efter det minsta elementet) kan parallelliseras genom att dela upp arrayen, söka efter det minsta elementet i varje delarray parallellt och slå samman mellanresultaten.

Selection Sort vs. Insertion Sort

Vilken algoritm är snabbare, Selection Sort eller Insertion Sort?

Låt oss jämföra mätningarna från mina Java-implementationer.

Jag lämnar det bästa fallet. Med Insertion Sort är tidskomplexiteten i bästa fall O(n) och tog mindre än en millisekund för upp till 524 288 element. Så i bästa fall är Insertion Sort, för alla antal element, flera storleksordningar snabbare än Selection Sort.

n	Selection Sort unsorterad	Insättningssortering unsorterad	Selection Sort nedåtgående	Insättningssortering nedåtgående
…	…	…	…	…
16.384	27,9 ms	21,9 ms	65,6 ms	43,6 ms
32.768	108,0 ms	87,9 ms	265,4 ms	175,8 ms
65.536	434,0 ms	350,4 ms	1.052,2 ms	697,6 ms
131.072	1.729,8 ms	1.398,9 ms	4.209,9 ms	2.840,0 ms
262.144	6.913,4 ms	5.706,8 ms	16.863,7 ms	11.517,4 ms
524.288	27.649,8 ms	23.009,7 ms	67.537,8 ms	46.309,3 ms

Och återigen som diagram:

Insertion Sort är därför inte bara snabbare än Selection Sort i bästa fall utan även i genomsnittligt och sämsta fall.

Anledningen till detta är att Insertion Sort i genomsnitt kräver hälften så många jämförelser. Som en påminnelse kan nämnas att med Insertion Sort har vi jämförelser och förskjutningar som i genomsnitt omfattar upp till hälften av de sorterade elementen; med Selection Sort måste vi söka efter det minsta elementet i alla osorterade element i varje steg.

Selection Sort har betydligt färre skrivoperationer, så Selection Sort kan vara snabbare när skrivoperationer är dyra. Detta är inte fallet med sekventiella skrivningar till matriser, eftersom dessa oftast sker i CPU-cachen.

I praktiken används Selection Sort därför nästan aldrig.

Sammanfattning

Selection Sort är en lätt att implementera, och i sin typiska implementering instabil, sorteringsalgoritm med en genomsnittlig, bästa och sämsta tidskomplexitet på O(n²).

Selection Sort är långsammare än Insertion Sort, varför den sällan används i praktiken.

Du hittar fler sorteringsalgoritmer i denna översikt över alla sorteringsalgoritmer och deras egenskaper i den första delen av artikelserien.

Om du gillade artikeln, dela den gärna med hjälp av en av delningsknapparna i slutet. Vill du bli informerad via e-post när jag publicerar en ny artikel? Använd då följande formulär för att prenumerera på mitt nyhetsbrev.