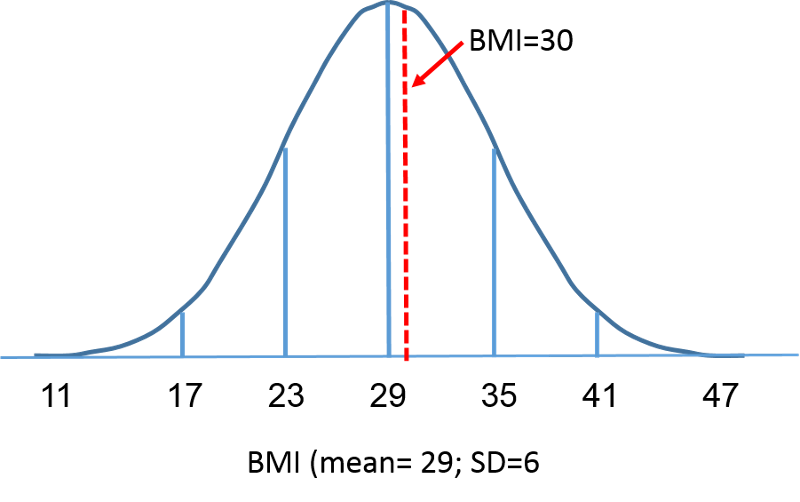
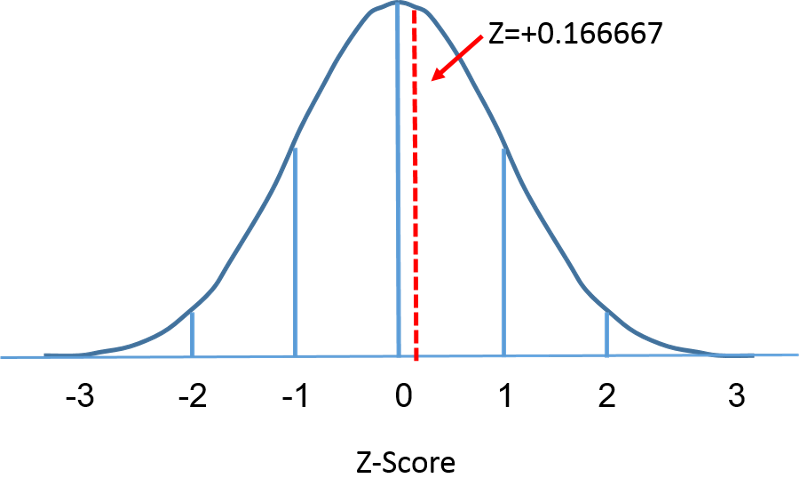
Standardnormalfördelningen är en normalfördelning med ett medelvärde på noll och en standardavvikelse på 1. Standardnormalfördelningen är centrerad på noll och graden av avvikelse från medelvärdet för ett givet mått ges av standardavvikelsen. För standardnormalfördelningen ligger 68 % av observationerna inom 1 standardavvikelse från medelvärdet, 95 % ligger inom 2 standardavvikelser från medelvärdet och 99,9 % ligger inom 3 standardavvikelser från medelvärdet. Hittills har vi använt ”X” för att beteckna den intressanta variabeln (t.ex. X=BMI, X=höjd, X=vikt). När vi använder en standardnormalfördelning kommer vi dock att använda ”Z” för att hänvisa till en variabel i samband med en standardnormalfördelning. Efter standardisering visas nedan att BMI=30 som diskuterades på föregående sida ligger 0,16667 enheter över medelvärdet 0 på standardnormalfördelningen till höger.
 ====
====
Då arean under standardkurvan = 1 kan vi börja definiera sannolikheterna för specifika observationer mer exakt. För varje given Z-score kan vi beräkna arean under kurvan till vänster om denna Z-score. Tabellen i ramen nedan visar sannolikheterna för standardnormalfördelningen. Undersök tabellen och notera att en Z-poäng på 0,0 anger en sannolikhet på 0,50 eller 50 %, och en Z-poäng på 1, dvs. en standardavvikelse över medelvärdet, anger en sannolikhet på 0,8413 eller 84 %. Detta beror på att en standardavvikelse över och under medelvärdet omfattar ungefär 68 % av området, så en standardavvikelse över medelvärdet motsvarar hälften av detta, dvs. 34 %. Så 50 % under medelvärdet plus 34 % över medelvärdet ger oss 84 %.
Sannolikheter för standardnormalfördelningen Z
![]()
Denna tabell är organiserad för att ge arean under kurvan till vänster om eller mindre än ett angivet värde eller ”Z-värde”. I det här fallet, eftersom medelvärdet är noll och standardavvikelsen är 1, är Z-värdet antalet standardavvikelseenheter från medelvärdet, och arean är sannolikheten för att observera ett värde som är mindre än det specifika Z-värdet. Observera också att tabellen visar sannolikheter med två decimaler av Z. Enhetsplatsen och den första decimalen visas i den vänstra kolumnen, och den andra decimalen visas tvärs över den översta raden.
Men låt oss återgå till frågan om sannolikheten för att BMI är mindre än 30, dvs. P(X<30). Vi kan besvara denna fråga med hjälp av den vanliga normalfördelningen. I figurerna nedan visas fördelningarna av BMI för män i 60-årsåldern och standardnormalfördelningen sida vid sida.
Fördelning av BMI och standardnormalfördelning
 ====
====
Området under varje kurva är ett men skalningen av X-axeln är olika. Observera dock att områdena till vänster om den streckade linjen är desamma. BMI-fördelningen sträcker sig från 11 till 47, medan den standardiserade normalfördelningen, Z, sträcker sig från -3 till 3. Vi vill beräkna P(X < 30). För att göra detta kan vi bestämma det Z-värde som motsvarar X = 30 och sedan använda den standardiserade normalfördelningstabellen ovan för att hitta sannolikheten eller arean under kurvan. Följande formel omvandlar ett X-värde till ett Z-värde, även kallat standardiserat värde:

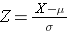
där μ är medelvärdet och σ är standardavvikelsen för variabeln X.
För att beräkna P(X < 30) omvandlar vi X=30 till motsvarande Z-poäng (detta kallas standardisering):

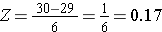
Sålunda är P(X < 30) = P(Z < 0,17). Vi kan sedan slå upp motsvarande sannolikhet för detta Z-värde i den vanliga normalfördelningstabellen, som visar att P(X < 30) = P(Z < 0,17) = 0,5675. Sannolikheten för att en man i 60-årsåldern har ett BMI under 30 är alltså 56,75 %.
Ett annat exempel
Vad är sannolikheten för att en man i 60-årsåldern har ett BMI som överstiger 35 om man använder samma fördelning för BMI? Med andra ord, vad är P(X > 35)? Återigen standardiserar vi:

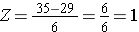
Vi går nu till tabellen för standardnormalfördelning för att söka upp P(Z>1) och för Z=1,00 finner vi att P(Z<1,00) = 0,8413. Observera dock att tabellen alltid anger sannolikheten för att Z är mindre än det angivna värdet, dvs. den ger oss P(Z<1)=0,8413.
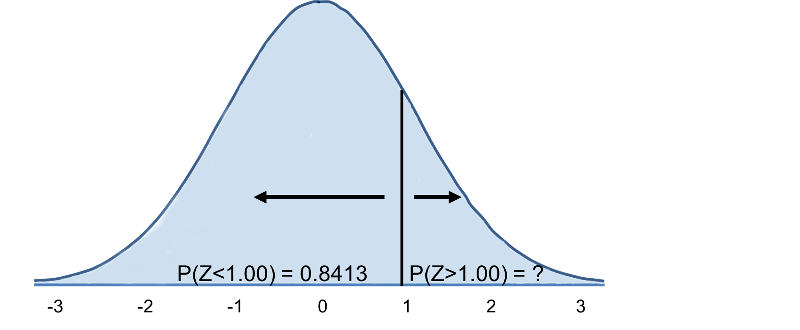
Därmed är P(Z>1)=1-0,8413=0,1587. Tolkning: Nästan 16 % av männen i 60-årsåldern har ett BMI över 35.
Normal sannolikhetsräknare
![]()
![]()
Z-poäng med R
Som ett alternativ till att leta upp normala sannolikheter i tabellen eller använda Excel kan vi använda R för att beräkna sannolikheter. Till exempel
> pnorm(0)
En Z-poäng på 0 (medelvärdet i en fördelning) har 50 % av ytan till vänster. Vad är sannolikheten för att en 60-årig man i populationen ovan har ett BMI som är lägre än 29 (medelvärdet)? Z-score skulle vara 0 och pnorm(0)=0,5 eller 50 %.
Vad är sannolikheten för att en 60-årig man har ett BMI som är lägre än 30? Z-score var 0,16667.
> pnorm(0,16667)
Så sannolikheten är 56,6 %.
Vad är sannolikheten för att en 60-årig man har ett BMI som är större än 35?
35-29=6, vilket är en standardavvikelse över medelvärdet. Vi kan alltså beräkna området till vänster
> pnorm(1)
och sedan subtrahera resultatet från 1,0.
1-0,8413447= 0,1586553
Så sannolikheten för att en 60-årig man ska ha ett BMI som är större än 35 är 15,8 %.
Och vi kan använda R för att beräkna det hela i ett enda steg enligt följande:
> 1-pnorm(1)
Sannolikhet för ett värdeintervall

Vad är sannolikheten för att en man på 60 år har ett BMI mellan 30 och 35? Observera att detta är samma sak som att fråga hur stor andel av män i 60-årsåldern som har ett BMI mellan 30 och 35. Närmare bestämt vill vi ha P(30 < X < 35)? Vi har tidigare beräknat P(30<X) och P(X<35); hur kan dessa två resultat användas för att beräkna sannolikheten för att BMI ligger mellan 30 och 35? Försök att formulera och svara på egen hand innan du tittar på förklaringen nedan.
Svar