
Växter kan växa nya celler i spiraler, som till exempel mönstret av frön i den här vackra solrosen.
Spiralen uppstår naturligt eftersom varje ny cell bildas efter en vändning.
”Ny cell, sedan vändning,
därefter ytterligare en cell, sedan vändning, …”
Hur långt ska man vända?
Om du var en växt, hur långt skulle du kunna svänga mellan nya celler?
Om du inte svänger alls får du en rak linje.
![]()
![]()
Men det är en mycket dålig konstruktion.Du vill ha något runt som håller ihop utan luckor.
Varför inte försöka hitta det bästa värdet för dig själv?
Prova olika värden, som 0,75, 0,9, 3,1416, 0,62 osv.
Håll dig i minnet att du försöker skapa ett mönster utan luckor från början till slut:
(Förresten spelar det ingen roll om den hela sifferdelen, som 1. eller 5. eftersom de är hela varv som pekar oss tillbaka i samma riktning.)
Vad fick du fram?
Om du fick fram något som slutar som 0,618 (eller 0,382, vilket är 1 – 0,618) så ”Grattis, du är en framgångsrik medlem av växtriket!”
 |
Det beror på att det gyllene snittet (1.61803…) är den bästa lösningen, och solrosen har upptäckt detta på sitt eget naturliga sätt. Prova … det borde se ut så här. |
Varför?
Varje tal som är en enkel bråkdel (exempel: 0.75 är 3/4, och 0,95 är 19/20 osv.) kommer efter ett tag att skapa ett mönster av linjer som staplas på varandra, vilket skapar luckor.
Men det gyllene snittet (dess symbol är den grekiska bokstaven Phi, som visas till vänster) är en expert på att inte vara något bråk.
Det är ett irrationellt tal (vilket innebär att vi inte kan skriva det som ett enkelt bråk), men mer än så … det är så långt vi kan komma från att vara nära något bråk.
| Det räcker inte med att bara vara irrationellt | |
|---|---|
 |
Pi (3,141592654…), som också är irrationellt. Olyckligtvis har den en decimal mycket nära 1/7 (= 0,142857…), så det slutar med 7 armar. |
 |
e (2,71828…), som också är irrationell, fungerar inte heller eftersom dess decimalvärde ligger nära 5/7 (0,714285…), så den slutar också med 7 armar. |
Hur fungerar det gyllene snittet?
| En av de speciella egenskaperna hos det gyllene snittet är att det kan definieras i termer av sig självt, så här: | |
| (I siffror: 1,61803… = 1 + 1/1/1,61803…) | |
| Det kan expanderas till det här bråket som fortsätter i all oändlighet (kallas ”fortsatt bråk”): | |
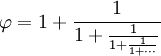 |
|
Det glider alltså snyggt in mellan enkla bråk.
Fibonacci-tal
Det finns ett särskilt förhållande mellan gyllene snittet och Fibonacci-talen (0, 1, 1, 1, 2, 3, 5, 8, 13, 21, … etc, varje tal är summan av de två föregående talen).
När vi tar två på varandra följande (efter varandra) Fibonacci-tal är deras förhållande mycket nära det gyllene snittet:
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
2
|
3
|
1.5 | |
|
3
|
5
|
1.666666666… | |
|
5
|
8
|
1.6 | |
|
8
|
13
|
1.625 | |
|
13
|
21
|
1.615384615… | |
|
…
|
…
|
… | |
|
144
|
233
|
1.618055556… | |
|
233
|
377
|
1.618025751… | |
|
…
|
…
|
… |

Så, precis som vi naturligt får sju armar när vi använder 0.142857 (1/7), tenderar vi att få Fibonacci-tal när vi använder det gyllene snittet.
Försök att räkna spiralarmarna – de ”vänstersvängande” spiralerna och sedan de ”högersvängande” spiralerna … vilka tal fick du?
Spiralformad bladtillväxt

Detta intressanta beteende finns inte bara i solrosfrön.
Löv, grenar och kronblad kan också växa i spiraler.
Varför? Så att nya blad inte blockerar solen för äldre blad, eller så att maximal mängd regn eller dagg leds ner till rötterna.
I själva verket tenderar rotationen när en växt har spiraler att vara en bråkdel som görs med två på varandra följande (efter varandra) Fibonacci-tal, till exempel:
- En halv rotation är 1/2 (1 och 2 är Fibonacci-tal)
- 3/5 är också vanligt förekommande (båda Fibonacci-tal), och
- 5/8 också (du gissade det!)
allt kommer närmare och närmare det gyllene snittet.
|
Och det är därför Fibonacci-talen är mycket vanliga i växter. Här är en tusensköna med 21 kronblad |
 |
Men vi ser inte detta hos alla växter, eftersom naturen har många olika metoder för att överleva.
Gyllene vinkeln
Sedan tidigare har vi talat om ”vändningar” (hela rotationer).
Äkvivalenten till 0,61803… rotationer är 222,4922… grader, eller ungefär 222,5°.
I andra riktningen är det ungefär 137,5°, vilket kallas ”den gyllene vinkeln”.
Så, nästa gång du går i trädgården, leta efter den gyllene vinkeln,
och räkna kronblad och blad för att hitta Fibonacci-tal,
och upptäck hur smarta växterna är … !
Övning
Varför går du inte ut i trädgården eller parken just nu och börjar räkna blad och kronblad och mäta rotationer för att se vad du hittar.
Du kan skriva dina resultat på det här formuläret:
| Plantans namn eller beskrivning: | ||||||
| Växer bladen i spiraler? Y / N | ||||||
| Räkna en grupp blad: | ||||||
| Hur många blad (a) ? | ||||||
| Hur många fullständiga rotationer (b) ? | ||||||
| Rotation per blad (b/a) : | ||||||
| Rotationsvinkel (360 × b/a) : | ||||||
| Finns det blommor? Y / N | ||||||
| Hur många kronblad på blomma 1: | ||||||
| 3: | ||||||
(Men kom ihåg att naturen har sina egna regler, och den behöver inte följa matematiska mönster,
men när den gör det är det fantastiskt att se.)
* Anteckningar om animationen
Solrosfrön växer från centrum och utåt, men i animationen tyckte jag att det var lättare att rita de yngre fröna först och sedan lägga till de äldre.
Animationen bör fortsätta längre för att vara lika lång som solrosen – detta skulle resultera i 55 spiraler medurs och 34 spiraler moturs (på varandra följande Fibonacci-tal). Jag ville bara inte att det skulle ta för lång tid.
Spiralerna är inte inprogrammerade i den – de uppstår naturligt som ett resultat av att försöka placera fröna så nära varandra som möjligt och samtidigt hålla dem i rätt rotation.

