Biografi
Johannes Kepler är nu främst ihågkommen för att ha upptäckt de tre lagarna för planetrörelse som bär hans namn och som publicerades 1609 och 1619.) Han utförde också viktiga arbeten inom optiken (1604, 1611), upptäckte två nya regelbundna polyeder (1619), gav den första matematiska behandlingen av tät packning av lika stora sfärer (vilket ledde till en förklaring av formen på cellerna i en honungskaka, 1611), gav det första beviset på hur logaritmer fungerade (1624), och utformade en metod för att hitta volymerna av roterande solida kroppar som (i efterhand!) kan ses som ett bidrag till utvecklingen av kalkylen (1615, 1616). Dessutom beräknade han de mest exakta astronomiska tabellerna som hittills varit kända, vars fortsatta noggrannhet bidrog i hög grad till att fastställa sanningen om den heliocentriska astronomin (Rudolphine Tables, Ulm, 1627).
En stor mängd av Keplers korrespondens finns bevarad. Många av hans brev motsvarar nästan en vetenskaplig uppsats (det fanns ännu inga vetenskapliga tidskrifter), och korrespondenterna verkar ha behållit dem för att de var intressanta. Följaktligen vet vi ganska mycket om Keplers liv och även om hans karaktär. Det är delvis på grund av detta som Kepler har haft något av en karriär som en mer eller mindre fiktiv karaktär (se historiografisk anmärkning nedan).
Kepler föddes i den lilla staden Weil der Stadt i Schwaben och flyttade till närliggande Leonberg med sina föräldrar 1576. Hans far var legosoldat och hans mor dotter till en värdshusägare. Johannes var deras första barn. Hans far lämnade hemmet för sista gången när Johannes var fem år och tros ha dött i kriget i Nederländerna. Som barn bodde Kepler tillsammans med sin mor i sin farfars värdshus. Han berättar att han brukade hjälpa till genom att betjäna på värdshuset. Man kan tänka sig att kunderna ibland var förbryllade över barnets ovanliga kompetens i aritmetik.
Keplers tidiga utbildning skedde i en lokal skola och sedan vid ett närliggande seminarium, varifrån han, med avsikt att bli prästvigd, skrev in sig vid universitetet i Tübingen, som då (liksom nu) var en bastion för luthersk ortodoxi.
Keplers åsikter
Under hela sitt liv var Kepler en djupt religiös man. Alla hans skrifter innehåller många hänvisningar till Gud, och han såg sitt arbete som en uppfyllelse av sin kristna plikt att förstå Guds verk. Eftersom människan, som Kepler trodde, var skapad till Guds avbild, var hon uppenbarligen kapabel att förstå det universum som han hade skapat. Dessutom var Kepler övertygad om att Gud hade skapat universum enligt en matematisk plan (en tro som återfinns i Platons verk och som förknippas med Pythagoras). Eftersom det vid den tiden var allmänt accepterat att matematiken var en säker metod för att komma fram till sanningar om världen (Euklides vanliga föreställningar och postulat ansågs faktiskt vara sanna), har vi här en strategi för att förstå universum. Eftersom vissa författare har gett Kepler ett namn för irrationalitet är det värt att notera att denna ganska hoppfulla epistemologi faktiskt ligger mycket långt ifrån mystikerns övertygelse om att saker och ting endast kan förstås på ett oprecist sätt som förlitar sig på insikter som inte är föremål för förnuftet. Kepler tackar visserligen upprepade gånger Gud för att han har gett honom insikter, men insikterna presenteras som rationella.
Universitetsutbildning
Vid denna tid var det vanligt att alla studenter vid ett universitet deltog i kurser i ”matematik”. I princip omfattade detta de fyra matematiska vetenskaperna: aritmetik, geometri, astronomi och musik. Det verkar dock som om vad som lärdes ut berodde på det aktuella universitetet. I Tübingen fick Kepler undervisning i astronomi av en av tidens ledande astronomer, Michael Mästlin (1550-1631). Den astronomi som stod på schemat var naturligtvis geocentrisk astronomi, det vill säga den aktuella versionen av det ptolemaiska systemet, där alla sju planeterna – månen, Merkurius, Venus, solen, Mars, Jupiter och Saturnus – rörde sig runt jorden och deras positioner i förhållande till fixstjärnorna beräknades genom att kombinera sina cirkelrörelser. Detta system överensstämde mer eller mindre med gängse (aristoteliska) uppfattningar om fysik, även om det fanns vissa svårigheter, t.ex. om man kunde betrakta en cirkelrörelse som ”enhetlig” (och därmed godtagbar som uppenbart evig) om den inte var enhetlig kring sitt eget centrum utan kring en annan punkt (kallad en ”ekvant”). Det verkar dock som om astronomerna (som såg sig själva som ”matematiker”) på det hela taget nöjde sig med att fortsätta att beräkna planeternas positioner och överlåta åt naturfilosoferna att bekymra sig om huruvida de matematiska modellerna motsvarade de fysiska mekanismerna. Kepler intog inte denna inställning. I hans tidigaste publicerade arbete (1596) föreslås att man ska ta hänsyn till planeternas faktiska banor, inte till de cirklar som används för att konstruera dem.
I Tübingen studerade Kepler inte bara matematik utan även grekiska och hebreiska (båda nödvändiga för att kunna läsa skrifterna på deras originalspråk). Undervisningen skedde på latin. I slutet av sitt första år fick Kepler A i allt utom matematik. Förmodligen försökte Mästlin tala om för honom att han kunde göra bättre ifrån sig, för Kepler var faktiskt en av de utvalda elever som han valde att lära ut mer avancerad astronomi genom att introducera dem till Copernicus nya, heliocentriska kosmologiska system. Det var från Mästlin som Kepler fick reda på att förordet till Om revolutionerna, där han förklarade att detta var ”bara matematik”, inte var skrivet av Kopernikus. Kepler tycks ha accepterat nästan omedelbart att det kopernikanska systemet var fysiskt sant; hans skäl för att acceptera det kommer att diskuteras i samband med hans första kosmologiska modell (se nedan).
Det verkar som om det redan under Keplers studietid fanns indikationer på att hans religiösa övertygelse inte helt överensstämde med den ortodoxa lutheranism som var rådande i Tübingen och som formulerades i Confessio Augustana Ⓣ. Keplers problem med denna protestantiska ortodoxi gällde det förmodade förhållandet mellan materia och ”ande” (en icke-materiell enhet) i läran om eukaristin. Detta anknyter till Keplers astronomi i så måtto att han tydligen fann något liknande intellektuella svårigheter i att förklara hur ”kraft” från solen kunde påverka planeterna. I sina skrifter är Kepler benägen att lägga sina åsikter på bordet – vilket är mycket bekvämt för historiker. I verkligheten verkar det troligt att en liknande tendens till öppenhet fick myndigheterna i Tübingen att hysa välgrundade tvivel om hans religiösa ortodoxi. Detta kan förklara varför Mästlin övertalade Kepler att överge planerna på prästvigning och i stället ta en tjänst som matematiklärare i Graz. Den religiösa intoleransen skärptes under de följande åren. Kepler exkommunicerades 1612. Detta orsakade honom mycket smärta, men trots sin (vid det laget) relativt höga sociala ställning som kejserlig matematiker lyckades han aldrig få förbudet upphävt.
Keplers första kosmologiska modell (1596)
Istället för de sju planeterna i den vanliga geocentriska astronomin hade det kopernikanska systemet endast sex, och månen hade blivit en kropp av ett slag som tidigare var okänd för astronomin och som Kepler senare skulle kalla för ”satellit” (ett namn som han myntade 1610 för att beskriva de månar som Galilei hade upptäckt kretsade kring Jupiter, och som bokstavligen betyder ”ledsagare”). Varför sex planeter?
I den geocentriska astronomin fanns det dessutom inget sätt att med hjälp av observationer ta reda på de relativa storlekarna på de planetariska kloten; man antog helt enkelt att de var i kontakt med varandra. Detta verkade inte kräva någon förklaring, eftersom det passade väl in i naturfilosofernas tro att hela systemet vändes från rörelsen av den yttersta sfären, en (eller kanske två) bortom de ”fasta” stjärnornas sfär (de vars mönster bildade konstellationerna), bortom Saturnus sfär. I det kopernikanska systemet gjorde det faktum att den årliga komponenten av varje planets rörelse var en återspegling av jordens årliga rörelse det möjligt att använda observationer för att beräkna storleken på varje planets bana, och det visade sig att det fanns enorma utrymmen mellan planeterna. Varför just dessa mellanrum?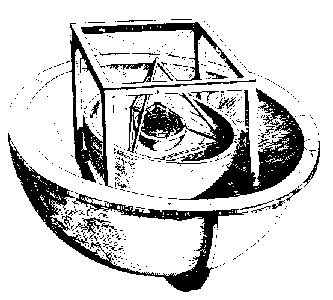
Keplers svar på dessa frågor, som beskrivs i hans Mysterium cosmographicum Ⓣ, Tübingen, 1596, ser bisarrt ut för 1900-talets läsare (se figuren till höger). Han föreslog att om en sfär ritades så att den berörde insidan av Saturnus bana, och en kub skrevs in i sfären, så skulle den sfär som skrevs in i kuben vara den sfär som omskriver Jupiters bana. Om sedan en regelbunden tetraeder ritades in i den sfär som beskriver Jupiters bana, skulle tetraederns insphere vara den sfär som beskriver Mars bana, och så vidare inåt, vilket skulle placera den regelbundna dodekaedern mellan Mars och jorden, den regelbundna isosaedern mellan jorden och Venus, och den regelbundna oktaedern mellan Venus och Merkurius. Detta förklarar antalet planeter perfekt: det finns bara fem konvexa regelbundna solider (vilket bevisas i Euklids element, bok 13). Det ger också en övertygande överensstämmelse med storleken på banorna enligt Kopernikus, där det största felet är mindre än 10 % (vilket är spektakulärt bra för en kosmologisk modell även nu). Kepler uttryckte sig inte i termer av procentuella fel, och hans modell är faktiskt den första matematiska kosmologiska modellen, men det är lätt att förstå varför han trodde att observationerna stödde hans teori.
Kepler såg sin kosmologiska teori som ett bevis för den kopernikanska teorin. Innan han presenterade sin egen teori gav han argument för att fastställa rimligheten i själva den kopernikanska teorin. Kepler hävdar att dess fördelar jämfört med den geocentriska teorin ligger i dess större förklaringskraft. Den kopernikanska teorin kan till exempel förklara varför Venus och Merkurius aldrig ses särskilt långt från solen (de ligger mellan jorden och solen) medan det i den geocentriska teorin inte finns någon förklaring till detta faktum. Kepler listar nio sådana frågor i det första kapitlet i Mysterium cosmographicum Ⓣ.
Kepler utförde detta arbete medan han undervisade i Graz, men boken sågs genom pressen i Tübingen av Mästlin. Överensstämmelsen med värden som härletts från observationer var inte exakt, och Kepler hoppades att bättre observationer skulle förbättra överensstämmelsen, så han skickade ett exemplar av Mysterium cosmographicum till en av tidens främsta observationsastronomer, Tycho Brahe (1546 – 1601). Tycho, som då arbetade i Prag (på den tiden det heliga romerska rikets huvudstad), hade faktiskt redan skrivit till Mästlin för att söka en matematisk assistent. Kepler fick jobbet.
”Kriget med Mars”
Naturligtvis var Tychos prioriteringar inte desamma som Keplers, och Kepler fick snart arbeta med det svårlösta problemet med Mars bana. Han fortsatte att arbeta med detta efter att Tycho dog (1601) och Kepler efterträdde honom som kejserlig matematiker. Konventionellt sett var banor sammansatta av cirklar, och det krävdes ganska få observationsvärden för att fastställa cirklarnas relativa radier och positioner. Tycho hade gjort ett stort antal observationer och Kepler bestämde sig för att utnyttja dem på bästa möjliga sätt. I huvudsak hade han så många observationer tillgängliga att när han väl hade konstruerat en möjlig bana kunde han kontrollera den mot ytterligare observationer tills en tillfredsställande överenskommelse nåddes. Kepler drog slutsatsen att Mars bana var en ellips med solen i ett av brännpunkterna (ett resultat som när det utvidgades till alla planeter nu kallas ”Keplers första lag”), och att en linje som förbinder planeten med solen svepte ut lika stora områden vid lika långa tidpunkter när planeten beskrev sin bana (”Keplers andra lag”), det vill säga att området används som ett mått på tid. Efter att detta arbete publicerades i Astronomia nova, … Ⓣ, Heidelberg, 1609, fann Kepler banor för de andra planeterna och fastställde därmed att de två lagarna gällde även för dem. Båda lagarna relaterar planetens rörelse till solen; Keplers kopernikanism var avgörande för hans resonemang och för hans slutsatser.
Den faktiska beräkningsprocessen för Mars var oerhört mödosam – det finns nästan tusen överlevande aritmetiska blad i folioformat – och Kepler själv hänvisar till detta arbete som ”mitt krig mot Mars”, men resultatet var en bana som stämmer överens med moderna resultat så exakt att jämförelsen måste ta hänsyn till sekulära förändringar i banan sedan Keplers tid.
Observationsfel
Det var avgörande för Keplers metod att kontrollera möjliga banor mot observationer att han hade en uppfattning om vad som skulle accepteras som tillräcklig överensstämmelse. Av detta följer den första uttryckliga användningen av begreppet observationsfel. Kepler kan ha fått detta begrepp åtminstone delvis av Tycho, som gjorde detaljerade kontroller av sina instrumenters prestanda (se biografin om Brahe).
Optik och den nya stjärnan 1604
Arbetet om Mars var i huvudsak slutfört 1605, men det blev förseningar när det gällde att få boken publicerad. Under tiden gjorde Kepler, som svar på oron över månens olika skenbara diameter när den observerades direkt och när den observerades med hjälp av en camera obscura, en del arbete om optik och kom med den första korrekta matematiska teorin om camera obscura och den första korrekta förklaringen av hur det mänskliga ögat fungerar, med en uppochnedvänd bild som bildas på näthinnan. Dessa resultat publicerades i Ad Vitellionem paralipomena, quibus astronomiae pars optica traditur Ⓣ, Frankfurt 1604. Han skrev också om den nya stjärnan 1604, som nu brukar kallas ”Keplers supernova”, där han förkastade ett flertal förklaringar och vid ett tillfälle anmärkte att denna stjärna naturligtvis bara kunde vara en speciell skapelse ”men innan vi kommer till tror jag att vi bör pröva allt annat.” De stella nova Ⓣ, Prag, 1606, kapitel 22, KGW 1, s. 257, rad 23.
Efter Galileos användning av teleskopet för att upptäcka Jupiters månar, som publicerades i hans Sidereal Messenger (Venedig, 1610), till vilken Kepler hade skrivit ett entusiastiskt svar (1610), skrev Kepler en studie av linsernas egenskaper (det första optiska arbetet av detta slag), i vilken han presenterade en ny utformning av teleskopet med två konvexa linser (Dioptrice, Prag, 1611). Denna konstruktion, där den slutliga bilden är inverterad, var så framgångsrik att den nu vanligtvis kallas inte för ett keplerskt teleskop utan helt enkelt för det astronomiska teleskopet.
Lämnar Prag för Linz
Keplers år i Prag var relativt lugna och vetenskapligt sett extremt produktiva. Faktum är att även när saker och ting gick dåligt tycks han aldrig ha låtit yttre omständigheter hindra honom från att fortsätta sitt arbete. Saker och ting började gå mycket dåligt i slutet av 1611. Först dog hans sjuåriga son. Kepler skrev till en vän att denna död var särskilt svår att bära eftersom barnet påminde honom så mycket om honom själv i den åldern. Sedan dog Keplers hustru. Då tvingades kejsar Rudolf, vars hälsa började svikta, att abdikera till förmån för sin bror Matthias, som i likhet med Rudolf var katolik men (till skillnad från Rudolf) inte trodde på tolerans mot protestanter. Kepler var tvungen att lämna Prag. Innan han reste lät han flytta sin hustrus kropp till sonens grav och skrev ett latinskt epitafium för dem. Han och hans kvarvarande barn flyttade till Linz (nu i Österrike).
Äktenskap och vinfat
Kepler verkar ha gift sig med sin första hustru, Barbara, av kärlek (även om äktenskapet arrangerades genom en mäklare). Det andra äktenskapet, 1613, var en fråga om praktisk nödvändighet; han behövde någon som kunde ta hand om barnen. Keplers nya hustru, Susanna, fick en snabbkurs i Keplers karaktär: i dediceringsbrevet till den bok som blev resultatet förklarar han att han under bröllopsfesten lade märke till att volymerna i vinfat uppskattades med hjälp av en stång som slogs in diagonalt genom sponten, och han började undra hur det kunde fungera. Resultatet blev en studie av volymerna hos solider av revolution Nova stereometria doliorum … Ⓣ, Linz, 1615, där Kepler, med utgångspunkt i Archimedes arbete, använde sig av en upplösning i ”odelbara”. Denna metod utvecklades senare av Bonaventura Cavalieri (ca 1598 – 1647) och är en del av anorna till infinitesimalkalkalkylen.
The Harmony of the World
Keplers huvuduppgift som kejserlig matematiker var att skriva astronomiska tabeller, baserade på Tychos observationer, men vad han egentligen ville göra var att skriva The Harmony of the World, som planerats sedan 1599 som en utveckling av hans Mysterium of the Cosmos. Detta andra verk om kosmologi (Harmonices mundi libri V Ⓣ, Linz, 1619) presenterar en mer genomarbetad matematisk modell än den tidigare, även om polyederna fortfarande finns kvar. Matematiken i detta arbete omfattar den första systematiska behandlingen av tessellationer, ett bevis för att det endast finns tretton konvexa enhetliga polyeder (de arkimediska soliderna) och den första redogörelsen för två icke-konvexa regelbundna polyeder (allt i bok 2). The Harmony of the World innehåller också det som nu är känt som ”Keplers tredje lag”, att för två planeter är förhållandet mellan kvadraterna på deras perioder samma som förhållandet mellan kuberna på de genomsnittliga radierna i deras banor. Från första början hade Kepler sökt efter en regel som relaterade banornas storlek till perioderna, men det fanns ingen långsam serie av steg mot denna lag som det hade funnits mot de andra två. Även om den tredje lagen spelar en viktig roll i några av de sista avsnitten i den tryckta versionen av Harmony of the World upptäcktes den faktiskt inte förrän verket var i tryck. Kepler gjorde revideringar i sista minuten. Han berättar själv historien om den slutliga framgången:
…och om ni vill ha det exakta ögonblicket i tiden, så tänkte jag ut den mentalt den åttonde mars i år ett tusen sexhundra och arton, men den underkastades en beräkning på ett olyckligt sätt, och förkastades därför som falsk, och återvände slutligen den femtonde maj och antog en ny angreppslinje, och stormade mitt sinnes mörker. Stödet från kombinationen av mitt sjuttonåriga arbete med Brahes observationer och den aktuella studien, som konspirerade tillsammans, var så starkt att jag först trodde att jag drömde och antog min slutsats bland mina grundläggande premisser. Men det är absolut säkert och exakt att ”proportionen mellan de periodiska tiderna för två planeter är just den sesquialterata proportionen av deras medelavstånd …”
(Harmonice mundi Book 5, Chapter 3, trans. Aiton, Duncan and Field, s. 411).
Häxprocess
Medans Kepler arbetade med sin Harmony of the World, anklagades hans mor för häxeri. Han tog hjälp av den juridiska fakulteten i Tübingen. Katharina Kepler släpptes så småningom, åtminstone delvis till följd av tekniska invändningar som berodde på att myndigheterna inte följde de korrekta rättsliga förfarandena vid användning av tortyr. De överlevande dokumenten är skrämmande. Kepler fortsatte dock att arbeta. I vagnen, på sin resa till Württemberg för att försvara sin mor, läste han ett arbete om musikteori av Vincenzo Galilei (ca 1520 – 1591, Galileos far), till vilket det finns många hänvisningar i The Harmony of the World.
Astronomiska tabeller
Att beräkna tabeller, det normala arbetet för en astronom, innebar alltid tung aritmetik. Kepler blev därför glad när han 1616 stötte på Napiers arbete om logaritmer (publicerat 1614). Mästlin sade dock genast till honom att det var olämpligt för en seriös matematiker att glädja sig åt ett enkelt räknehjälpmedel och att det var oklokt att lita på logaritmerna eftersom ingen förstod hur de fungerade. (Liknande kommentarer gjordes om datorer i början av 1960-talet.) Keplers svar på den andra invändningen var att publicera ett bevis på hur logaritmer fungerade, baserat på en oklanderligt respektabel källa: Euklids element, bok 5. Kepler beräknade tabeller med åttasiffriga logaritmer som publicerades med Rudolphine Tables (Ulm, 1628). I de astronomiska tabellerna användes inte bara Tychos observationer utan även Keplers två första lagar. Alla astronomiska tabeller som använde sig av nya observationer var exakta under de första åren efter publiceringen. Det som var anmärkningsvärt med Rudolphine-tabellerna var att de visade sig vara exakta under årtionden. Och när åren hopade sig, sågs naturligtvis tabellernas fortsatta noggrannhet som ett argument för att Keplers lagar var korrekta, och därmed för att den heliocentriska astronomin var korrekt. Keplers uppfyllande av sin tråkiga officiella uppgift som kejserlig matematiker ledde till att hans käraste önskan gick i uppfyllelse, nämligen att hjälpa till att etablera kopernikanismen.
Wallenstein
När Rudolftabellerna publicerades arbetade Kepler faktiskt inte längre för kejsaren (han hade lämnat Linz 1626), utan för Albrecht von Wallenstein (1583 – 1632), en av de få framgångsrika militära ledarna i trettioåriga kriget (1618 – 1648).
Wallenstein förväntade sig, precis som kejsar Rudolf, att Kepler skulle ge honom råd baserade på astrologi. Kepler var naturligtvis tvungen att lyda, men påpekar upprepade gånger att han inte tror att exakta förutsägelser kan göras. Liksom de flesta människor på den tiden accepterade Kepler astrologins princip, att himlakroppar kunde påverka vad som hände på jorden (de tydligaste exemplen är solen som orsakade årstiderna och månen som orsakade tidvattnet), men som kopernikanare trodde han inte på konstellationernas fysiska verklighet. Hans astrologi baserades endast på vinklarna mellan himlakropparnas positioner (”astrologiska aspekter”). Han uttrycker ett fullständigt förakt för den konventionella astrologins komplicerade system.
Död
Kepler dog i Regensburg efter en kort sjukdom. Han vistades i staden på väg för att hämta ut pengar som han var skyldig honom i samband med Rudolphine-tabellerna. Han begravdes i den lokala kyrkan, men denna förstördes under trettioåriga kriget och ingenting återstår av graven.
Historiografisk anmärkning
Mycket har ibland gjorts av förment icke-rationella inslag i Keplers vetenskapliga verksamhet. Troende astrologer hävdar ofta att hans arbete utgör en vetenskapligt respektabel föregångare till deras eget arbete. I sin inflytelserika Sleepwalkers gjorde den framlidne Arthur Koestler Keplers kamp med Mars till ett argument för den moderna vetenskapens inneboende irrationalitet. Det har funnits många tysta anhängare av dessa två övertygelser. Båda bygger dock på en mycket partiell läsning av Keplers verk. I synnerhet verkar Koestler inte ha haft den matematiska expertisen för att förstå Keplers tillvägagångssätt. Närmare studier visar att Koestler helt enkelt hade fel i sin bedömning.
Det verkligt viktiga icke-rationella elementet i Keplers arbete är hans kristendom. Keplers omfattande och framgångsrika användning av matematik får hans arbete att se ”modernt” ut, men vi har i själva verket att göra med en kristen naturfilosof, för vilken förståelsen av universums natur innebar att förstå dess skapares natur.