Selection Sort – Algoritm, cod sursă, complexitate în timp

Acest articol face parte din seria „Algoritmi de sortare: Ultimate Guide” și…

• descrie cum funcționează Selection Sort,
• include codul sursă Java pentru Selection Sort,
• arată cum se poate obține complexitatea în timp a acestuia (fără calcule matematice complicate)
• și verifică dacă performanța implementării Java corespunde comportamentului așteptat în timpul execuției.

Codul sursă pentru întreaga serie de articole îl puteți găsi în depozitul meu GitHub.

Exemplu: Sortarea cărților de joc

Sortarea cărților de joc în mână este exemplul clasic pentru Insertion Sort.

Selection Sort poate fi, de asemenea, ilustrat cu cărți de joc. Nu cunosc pe nimeni care să își aleagă cărțile în acest fel, dar ca exemplu, funcționează destul de bine 😉

În primul rând, așezați toate cărțile cu fața în sus pe masa din fața dvs. Cauți cea mai mică carte și o iei în stânga mâinii tale. Apoi căutați următoarea carte mai mare și o plasați în dreapta celei mai mici, și așa mai departe până când, în cele din urmă, luați cea mai mare carte din extrema dreaptă.

Diferență față de Insertion Sort

Cu Insertion Sort, am luat următoarea carte nesortată și am introdus-o în poziția corectă în cărțile sortate.

Selection Sort funcționează cam invers: Selectăm cea mai mică carte din cărțile nesortate și apoi – una după alta – o adăugăm la cărțile deja sortate.

Algoritmul sortării prin selecție

Algoritmul poate fi explicat cel mai simplu printr-un exemplu. În următorii pași, arăt cum se sortează tabloul cu Selection Sort:

Pasul 1

Divizăm tabloul într-o parte stângă, sortată, și o parte dreaptă, nesortată. Partea sortată este goală la început:

Etapa 2

Cercăm cel mai mic element din partea dreaptă, nesortată. Pentru a face acest lucru, ne amintim mai întâi de primul element, care este 6. Trecem la câmpul următor, unde găsim un element și mai mic în 2. Mergem peste restul tabloului, căutând un element și mai mic. Din moment ce nu găsim niciunul, rămânem cu 2. Îl punem în poziția corectă, schimbându-l cu elementul de pe primul loc. Apoi mutăm granița dintre secțiunile tabloului cu un câmp spre dreapta:

Pasul 3

Cercăm din nou în partea dreaptă, nesortată, pentru cel mai mic element. De data aceasta este 3; îl interschimbăm cu elementul de pe poziția a doua:

Pasul 4

Încă o dată căutăm cel mai mic element în partea dreaptă. Este vorba de 4, care se află deja în poziția corectă. Așadar, nu este nevoie de operația de permutare în acest pas și doar mutăm marginea secțiunii:

Pasul 5

Ca cel mai mic element, găsim 6. Îl schimbăm cu elementul de la începutul părții drepte, 9:

Pasul 6

Dintre cele două elemente rămase, 7 este cel mai mic. Îl schimbăm cu 9:

Algoritm Finished

Ultimul element este automat cel mai mare și, prin urmare, se află în poziția corectă. Algoritmul este terminat, iar elementele sunt sortate:

Codul sursă Java Selection Sort

În această secțiune, veți găsi o implementare Java simplă a Selection Sort.

Bucla exterioară iterază peste elementele care trebuie sortate și se termină după penultimul element. Atunci când acest element este sortat, ultimul element este și el sortat automat. Variabila de buclă i indică întotdeauna primul element din partea dreaptă, nesortată.

În fiecare ciclu de buclă, primul element din partea dreaptă este presupus inițial ca fiind cel mai mic element min; poziția sa este memorată în minPos.

Bucla interioară itera apoi de la al doilea element al părții drepte până la sfârșitul acesteia și realocă min și minPos ori de câte ori se găsește un element și mai mic.

După ce bucla interioară a fost finalizată, elementele din pozițiile i (începutul părții drepte) și minPos sunt schimbate (cu excepția cazului în care acestea sunt același element).

public class SelectionSort { public static void sort(int elements) { int length = elements.length; for (int i = 0; i < length - 1; i++) { // Search the smallest element in the remaining array int minPos = i; int min = elements; for (int j = i + 1; j < length; j++) { if (elements < min) { minPos = j; min = elements; } } // Swap min with element at pos i if (minPos != i) { elements = elements; elements = min; } } }}

Codul prezentat diferă de clasa SelectionSort din depozitul GitHub prin faptul că implementează interfața SortAlgorithm pentru a fi ușor de interschimbat în cadrul de testare.

Complexitatea de timp a sortării selecției

Notăm cu n numărul de elemente, în exemplul nostru n = 6.

Cele două bucle imbricate sunt un indiciu că avem de-a face cu o complexitate de timp* de O(n²). Acesta va fi cazul dacă ambele bucle iterază până la o valoare care crește liniar cu n.

Este evident cazul buclei exterioare: ea numără până la n-1.

Ce se întâmplă cu bucla interioară?

Vezi următoarea ilustrație:

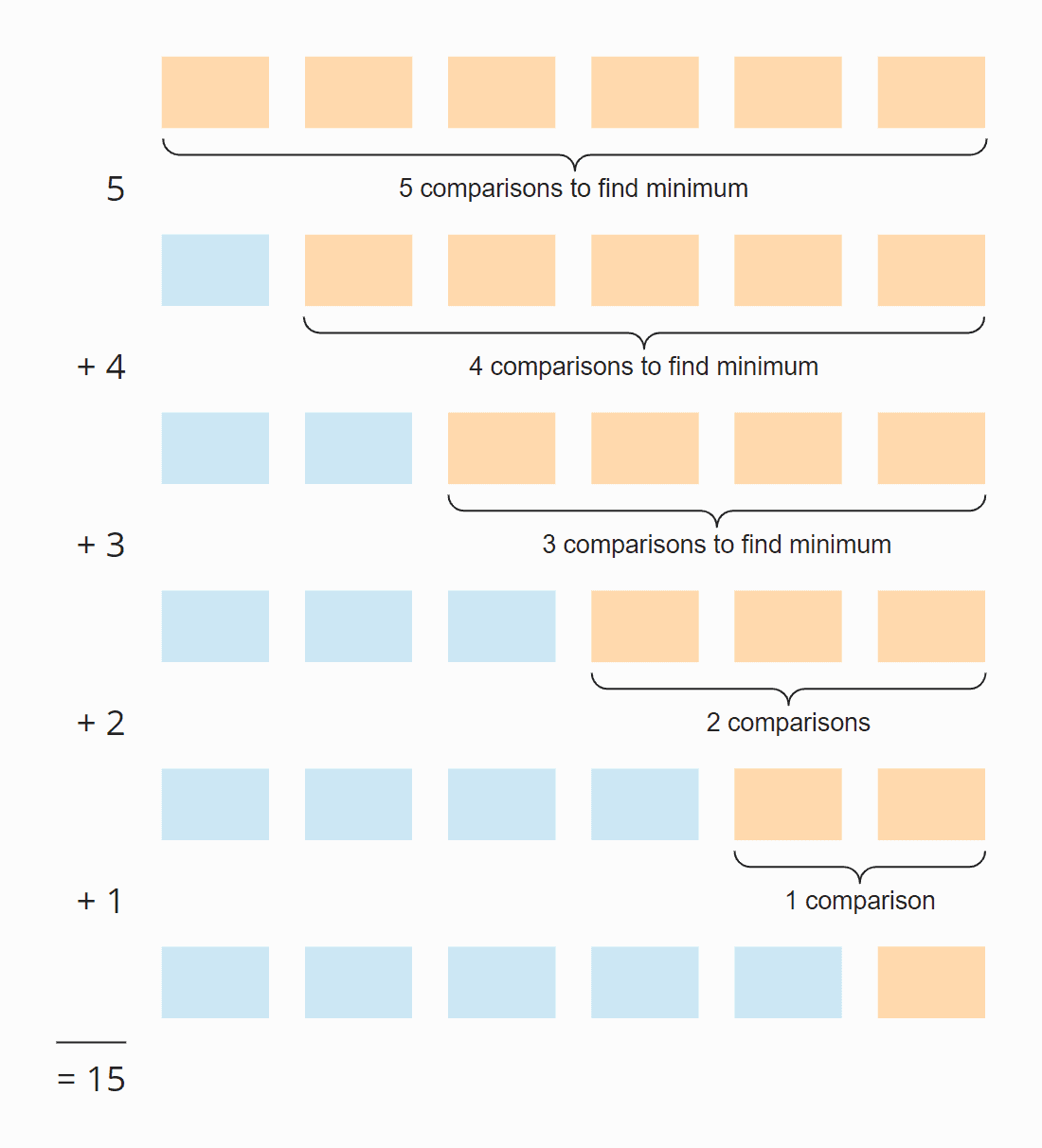
În fiecare pas, numărul de comparații este cu unul mai mic decât numărul de elemente nesortate. În total, există 15 comparații – indiferent dacă array-ul este inițial sortat sau nu.

Acest lucru poate fi calculat, de asemenea, după cum urmează:

Șase elemente înmulțit cu cinci pași; împărțit la doi, deoarece, în medie pe toți pașii, jumătate din elemente sunt încă nesortate:

6 × 5 × ½ = 30 × ½ = 15

Dacă înlocuim 6 cu n, obținem

n × (n – 1) × ½

După ce se înmulțește, rezultă:

½ n² – ½ n

Puterea cea mai mare a lui n în acest termen este n². Complexitatea de timp pentru căutarea celui mai mic element este, prin urmare, O(n²) – numit și „timp pătratic”.

Să ne uităm acum la schimbarea elementelor. În fiecare pas (cu excepția ultimului), se schimbă fie un element, fie niciunul, în funcție de faptul dacă cel mai mic element se află deja în poziția corectă sau nu. Astfel, avem, în total, un maxim de n-1 operații de permutare, adică complexitatea în timp de O(n) – numită și „timp liniar”.

Pentru complexitatea totală, doar clasa de complexitate cea mai mare contează, prin urmare:

Complexitatea în timp medie, în cel mai bun caz și în cel mai rău caz a Selection Sort este:

Complexitatea în timp medie, în cel mai bun caz și în cel mai rău caz a Selection Sort este: O(n²)

*Termenii „complexitate în timp” și „O-notație” sunt explicați în acest articol folosind exemple și diagrame.

Runtime of the Java Selection Sort Example

Suficientă teorie! Am scris un program de testare care măsoară timpul de execuție al Selection Sort (și al tuturor celorlalți algoritmi de sortare abordați în această serie) după cum urmează:

• Numărul de elemente de sortat se dublează după fiecare iterație, de la 1.024 elemente inițial până la 536.870.912 (= 229) elemente. O matrice de două ori mai mare decât această dimensiune nu poate fi creată în Java.
• Dacă un test durează mai mult de 20 de secunde, matricea nu este extinsă în continuare.
• Toate testele se execută cu elemente nesortate, precum și cu elemente pre-sortate ascendent și descendent.
• Permitem compilatorului HotSpot să optimizeze codul cu două runde de încălzire. După aceea, testele se repetă până când procesul este abandonat.

După fiecare iterație, programul tipărește mediana tuturor rezultatelor măsurătorilor anterioare.

Iată rezultatul pentru Selection Sort după 50 de iterații (de dragul clarității, acesta este doar un extras; rezultatul complet poate fi găsit aici):

n	nu este sortat	ascendent	descendent
….	…	…	…
16.384	27,9 ms	26,8 ms	65,6 ms
32.768	108,0 ms	105,4 ms	265,4 ms
65.536	434,0 ms	424,3 ms	1.052,2 ms
1.072	1.729,8 ms	1.714,1 ms	4.209,9 ms
262.144	6.913,4 ms	6.880,2 ms	16.863,7 ms
524.288	27.649,8 ms	27.568,7 ms	67.537,8 ms

Iată măsurătorile încă o dată sub formă de diagramă (prin care am afișat „nesortat” și „ascendent” ca o singură curbă datorită valorilor aproape identice):

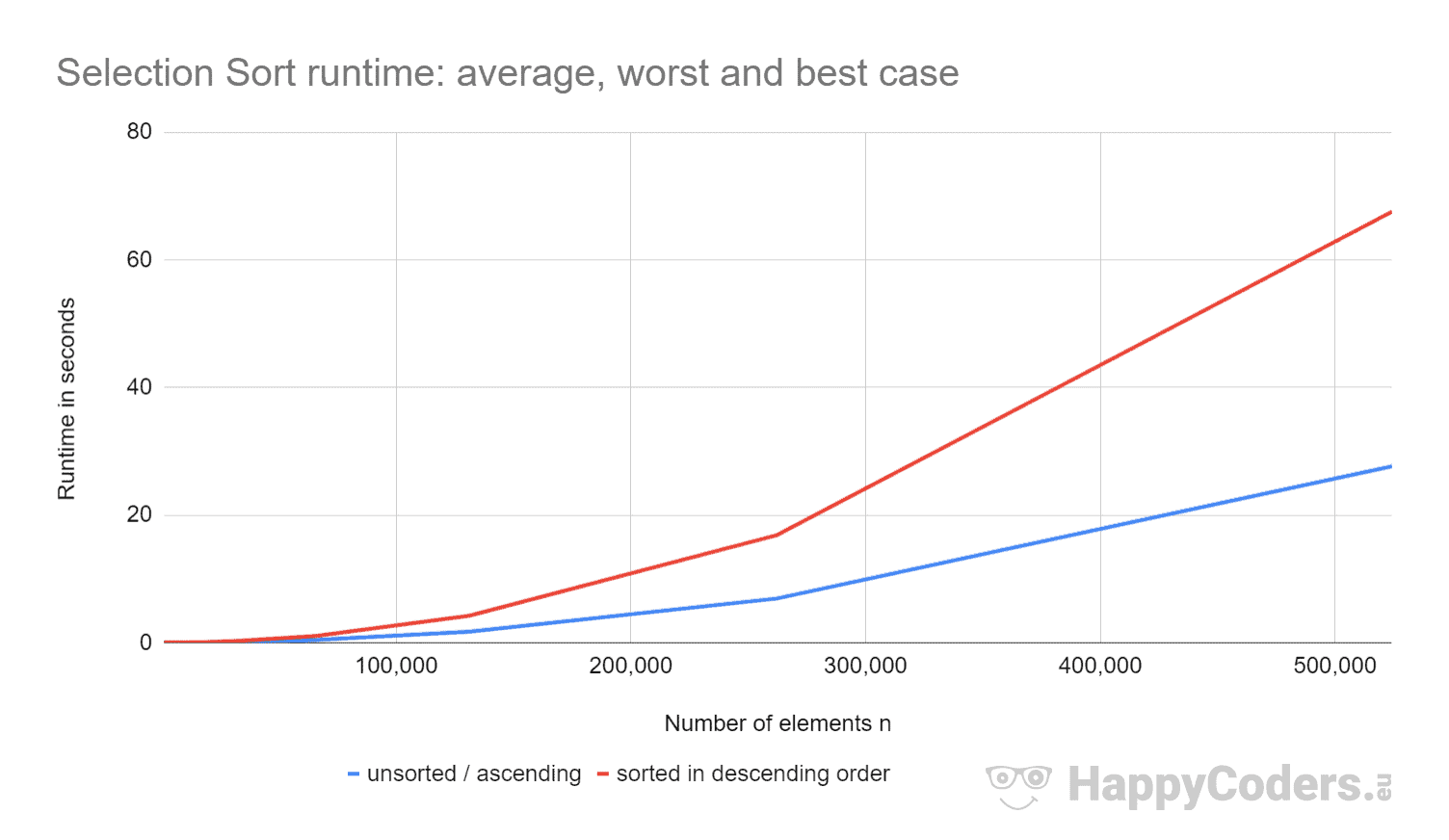
Este bine de văzut că

• dacă se dublează numărul de elemente, timpul de execuție este aproximativ de patru ori mai mare – indiferent dacă elementele sunt sau nu sortate în prealabil. Acest lucru corespunde complexității temporale așteptate de O(n²).
• că timpul de execuție pentru elementele sortate crescător este puțin mai bun decât pentru elementele nesortate. Acest lucru se datorează faptului că operațiile de permutare, care – după cum s-a analizat mai sus – au o importanță redusă, nu sunt necesare în acest caz.
• că timpul de execuție pentru elementele sortate descrescător este semnificativ mai rău decât pentru elementele nesortate.

De ce se întâmplă acest lucru?

Analiza timpului de execuție în cel mai rău caz

Teoretic, căutarea celui mai mic element ar trebui să dureze întotdeauna același timp, indiferent de situația inițială. Iar operațiunile de schimb ar trebui să fie doar puțin mai multe pentru elementele sortate în ordine descrescătoare (pentru elementele sortate în ordine descrescătoare, fiecare element ar trebui să fie schimbat; pentru elementele nesortate, aproape fiecare element ar trebui să fie schimbat).

Utilizând programul CountOperations din depozitul meu GitHub, putem vedea numărul diferitelor operațiuni. Iată rezultatele pentru elementele nesortate și elementele sortate în ordine descrescătoare, rezumate într-un singur tabel:

.

n	Comparații	Împărțiri neorânduite	Împărțiri în ordine descrescătoare	Împărțiri în ordine descrescătoare	minPos/min unsorted	minPos/min descending
…	…	…	…	…	…
512	130.816	504	256	2.866	66.047
1.024	523.776	1.017	512	6.439	263.167
2.048	2.096.128	2.042	1.024	14.727	1.050.623
4.096	8.386.560	4.084	2.048	30.758	4.198.399
8.192	33.550.336	8.181	4.096	69.378	16.785.407

Din valorile măsurate se poate observa:

• Cu elementele sortate în ordine descrescătoare, avem – așa cum era de așteptat – la fel de multe operații de comparație ca și cu elementele nesortate – adică n × (n-1) / 2.
• Cu elemente nesortate, avem – așa cum se presupune – aproape la fel de multe operații de schimb ca și elementele: de exemplu, cu 4.096 de elemente nesortate, există 4.084 de operații de schimb. Aceste numere se schimbă aleatoriu de la un test la altul.
• Cu toate acestea, cu elemente sortate în ordine descrescătoare, avem doar jumătate din numărul de operații de swap decât de elemente! Acest lucru se datorează faptului că, atunci când facem swap, nu numai că punem cel mai mic element la locul potrivit, ci și partenerul de swap respectiv.

Cu opt elemente, de exemplu, avem patru operații de swap. În primele patru iterații, avem câte una de fiecare dată, iar în iterațiile de la cinci la opt, niciuna (cu toate acestea, algoritmul continuă să ruleze până la sfârșit):

În plus, putem citi din măsurători:

• Motivul pentru care Selection Sort este mult mai lent cu elemente sortate în ordine descrescătoare poate fi găsit în numărul de asignări de variabile locale (minPos și min) atunci când căutăm cel mai mic element. În timp ce cu 8.192 de elemente nesortate avem 69.378 de astfel de asignări, cu elemente sortate în ordine descrescătoare, există 16.785.407 astfel de asignări – adică de 242 de ori mai multe!

De ce această diferență uriașă?

Analiza timpului de execuție a căutării celui mai mic element

Pentru elementele sortate în ordine descrescătoare, ordinea de mărime poate fi derivată din ilustrația de mai sus. Căutarea celui mai mic element se limitează la triunghiul format din cutiile portocalie și portocalie-albastră. În partea superioară portocalie, numerele din fiecare căsuță devin mai mici; în partea dreaptă portocaliu-albastră, numerele cresc din nou.

Operațiile de atribuire au loc în fiecare căsuță portocalie și în prima dintre căsuțele portocalie-albastră. Numărul de operații de atribuire pentru minPos și min este astfel, la figurat vorbind, de aproximativ „un sfert de pătrat” – matematic și precis, este ¼ n² + n – 1.

Pentru elementele nesortate, ar trebui să pătrundem mult mai adânc în problemă. Acest lucru ar depăși nu numai scopul acestui articol, ci și al întregului blog.

De aceea, îmi limitez analiza la un mic program demonstrativ care măsoară câte atribuții minPos/min există atunci când se caută cel mai mic element dintr-o matrice nesortată. Iată valorile medii după 100 de iterații (un mic extras; rezultatele complete pot fi găsite aici):

n	numărul mediu de asigurări minPos/min
1.024	7.08
4.096	8.61
16.385	8.94
65.536	11.81
262.144	12.22
1.048.576	14.26
4.194.304	14.71
16.777.216	16.44
67.108.864	17.92
268.435.456	20.27

Iată ca o diagramă cu axa x logaritmică:

Graficul arată foarte bine că avem o creștere logaritmică, adică, la fiecare dublare a numărului de elemente, numărul de atribuții crește doar cu o valoare constantă. După cum am spus, nu voi intra mai adânc în fundamentele matematice.

Acesta este motivul pentru care aceste asignări minPos/min sunt puțin semnificative în array-urile nesortate.

Alte caracteristici ale sortării prin selecție

În următoarele secțiuni, voi discuta despre complexitatea spațială, stabilitatea și paralelizabilitatea sortării prin selecție.

Complexitatea spațială a Selection Sort

Complexitatea spațială a Selection Sort este constantă, deoarece nu avem nevoie de spațiu de memorie suplimentar în afară de variabilele de buclă i și j și de variabilele auxiliare length, minPos și min.

Acest lucru înseamnă că, indiferent de numărul de elemente pe care le sortăm – zece sau zece milioane – nu avem nevoie decât de aceste cinci variabile suplimentare. Notăm timpul constant ca fiind O(1).

Stabilitatea sortării prin selecție

Selection Sort pare stabil la prima vedere: Dacă partea nesortată conține mai multe elemente cu aceeași cheie, primul ar trebui să fie anexat mai întâi la partea sortată.

Dar aparențele sunt înșelătoare. Deoarece prin schimbarea a două elemente în a doua sub-etapă a algoritmului, se poate întâmpla ca anumite elemente din partea nesortată să nu mai aibă ordinea inițială. Acest lucru, la rândul său, duce la faptul că ele nu mai apar în ordinea inițială în partea sortată.

Un exemplu poate fi construit foarte simplu. Să presupunem că avem două elemente diferite cu cheia 2 și unul cu cheia 1, aranjate după cum urmează, și apoi le sortăm cu Selection Sort:

În prima etapă, primul și ultimul element sunt schimbate. Astfel, elementul „DOUĂ” ajunge în spatele elementului „doi” – ordinea celor două elemente este schimbată.

În al doilea pas, algoritmul compară cele două elemente din spate. Ambele au aceeași cheie, 2. Deci niciun element nu este schimbat.

În al treilea pas, rămâne un singur element; acesta este considerat automat sortat.

Cele două elemente cu cheia 2 au fost astfel schimbate în ordinea lor inițială – algoritmul este instabil.

Variantă stabilă a sortării prin selecție

Selection Sort poate fi făcut stabil nu prin schimbarea celui mai mic element cu primul în pasul doi, ci prin deplasarea tuturor elementelor dintre primul și cel mai mic element cu o poziție spre dreapta și inserarea celui mai mic element la început.

Chiar dacă complexitatea în timp va rămâne aceeași datorită acestei modificări, deplasările suplimentare vor duce la o degradare semnificativă a performanței, cel puțin atunci când sortăm un array.

Cu o listă legată, tăierea și lipirea elementului care urmează să fie sortat ar putea fi făcută fără o pierdere semnificativă de performanță.

Paralelizabilitatea sortării prin selecție

Nu putem paraleliza bucla exterioară deoarece aceasta schimbă conținutul tabloului la fiecare iterație.

Bucla interioară (căutarea celui mai mic element) poate fi paralelizată prin divizarea tabloului, căutarea în paralel a celui mai mic element din fiecare subarray și fuzionarea rezultatelor intermediare.

Selection Sort vs. Insertion Sort

Care algoritm este mai rapid, Selection Sort sau Insertion Sort?

Să comparăm măsurătorile din implementările mele Java.

Lăsăm la o parte cel mai bun caz. Cu Insertion Sort, complexitatea timpului în cel mai bun caz este O(n) și a durat mai puțin de o milisecundă pentru până la 524.288 de elemente. Așadar, în cel mai bun caz, Insertion Sort este, pentru orice număr de elemente, cu câteva ordine de mărime mai rapid decât Selection Sort.

n	Selection Sort unsorted	Insertion Sort unsorted	Selection Sort descending	Insertion Sort descending
…	….	…	…	…
16.384	27,9 ms	21,9 ms	65,6 ms	43,6 ms
32.768	108,0 ms	87,9 ms	265,4 ms	175,8 ms
65.536	434,0 ms	350,4 ms	1.052,2 ms	697,6 ms
131.072	1.729,8 ms	1.398,9 ms	4.209,9 ms	2.840,0 ms
262.144	6.913,4 ms	5.706,8 ms	16.863,7 ms	11.517,4 ms
524.288	27.649,8 ms	23.009,7 ms	67.537,8 ms	46.309,3 ms

Și încă o dată ca o diagramă:

Insertion Sort este, prin urmare, nu numai mai rapid decât Selection Sort în cel mai bun caz, ci și în cazul mediu și în cel mai rău caz.

Motivul pentru aceasta este că Insertion Sort necesită, în medie, jumătate din numărul de comparații. Ca o reamintire, cu Insertion Sort, avem comparații și deplasări care reprezintă în medie până la jumătate din elementele sortate; cu Selection Sort, trebuie să căutăm cel mai mic element din toate elementele nesortate în fiecare etapă.

Selection Sort are semnificativ mai puține operații de scriere, astfel că Selection Sort poate fi mai rapid atunci când operațiile de scriere sunt costisitoare. Acesta nu este cazul scrierilor secvențiale în array-uri, deoarece acestea se realizează în cea mai mare parte în memoria cache a procesorului.

În practică, Selection Sort nu este, prin urmare, aproape niciodată utilizat.

Rezumat

Selection Sort este un algoritm de sortare ușor de implementat și, în implementarea sa tipică, instabil, cu o complexitate în timp medie, în cel mai bun caz și în cel mai rău caz de O(n²).

Selection Sort este mai lent decât Insertion Sort, motiv pentru care este rareori folosit în practică.

Vă veți găsi mai mulți algoritmi de sortare în această prezentare generală a tuturor algoritmilor de sortare și a caracteristicilor lor în prima parte a seriei de articole.

Dacă v-a plăcut articolul, nu ezitați să îl distribuiți folosind unul dintre butoanele de distribuire de la sfârșit. Doriți să fiți informat prin e-mail atunci când public un nou articol? Atunci folosiți următorul formular pentru a vă abona la newsletter-ul meu.

.