O ecuație sub forma pantă-intercepție se scrie sub forma
$$y=mx+b$$$
Unde m este panta dreptei și b este intercepția lui y. Puteți folosi această ecuație pentru a scrie o ecuație dacă știți panta și interceptarea y.
Exemplu
Găsește ecuația dreptei
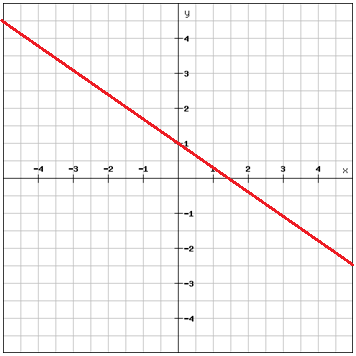
Alege două puncte care se află pe dreaptă
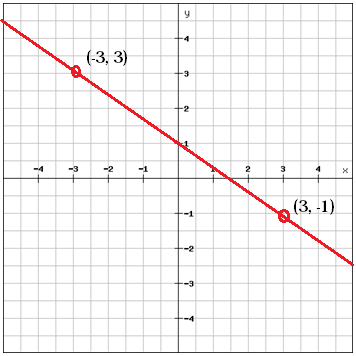
Calculează panta între cele două puncte
$$m=\frac{y_{2}\, -y_{1}}}{x_{2}\, -x_{1}}}=\frac{\left (-1 \right )-3}{3-\left ( -3 \right )}=\frac{-4}{6}=\frac{-2}{3}$$
Potem afla valoarea lui b, intersecția y, uitându-ne la grafic
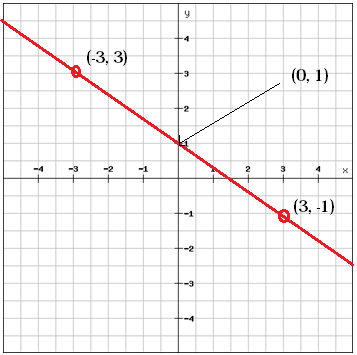
b = 1
Avem o valoare pentru m și o valoare pentru b. Aceasta ne dă funcția liniară
$$y=-\frac{2}{3}x+1$$
În multe cazuri, valoarea lui b nu este la fel de ușor de citit. În aceste cazuri, sau dacă nu sunteți sigur dacă dreapta traversează într-adevăr axa y în acest punct anume, puteți calcula b rezolvând ecuația pentru b și apoi înlocuind x și y cu unul dintre cele două puncte.
Potem folosi exemplul de mai sus pentru a ilustra acest lucru. Avem cele două puncte (-3, 3) și (3, -1). Din aceste două puncte am calculat panta
$$m=-\frac{2}{3}$$
Aceasta ne dă ecuația
$y=-\frac{2}{3}x+b$$
De aici putem rezolva ecuația pentru b
$b=y+\frac{2}{3}x$$
Și dacă introducem valorile din primul nostru punct (-3, 3) obținem
$$b=3+\frac{2}{3}\cdot \stânga ( -3 \dreapta )=3+\stânga ( -2 \dreapta )=1$$$
Dacă introducem această valoare pentru b în ecuație obținem
$y=-\frac{2}{3}x+1$$
care este aceeași ecuație pe care am obținut-o când am citit intersecția y din grafic.
Pentru a rezuma modul de scriere a unei ecuații liniare folosind forma pantă-intercepție, trebuie
- Identificați panta, m. Acest lucru se poate face calculând panta între două puncte cunoscute ale dreptei folosind formula pantei.
- Găsiți interceptarea y. Acest lucru se poate face înlocuind panta și coordonatele unui punct (x, y) de pe dreaptă în formula panta-intercepta pantei și apoi rezolvând pentru b.
După ce ați obținut atât m cât și b puteți să le puneți în ecuație la poziția lor respectivă.
Lecție video
Găsește ecuația graficului
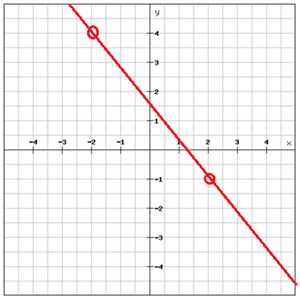
.