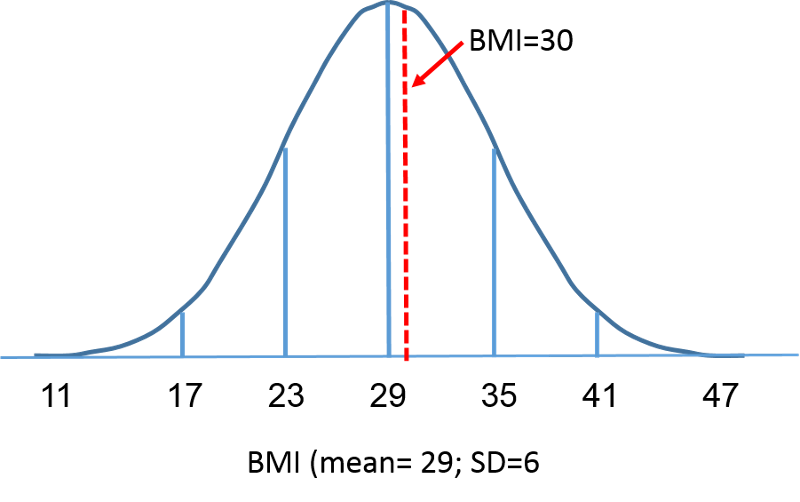
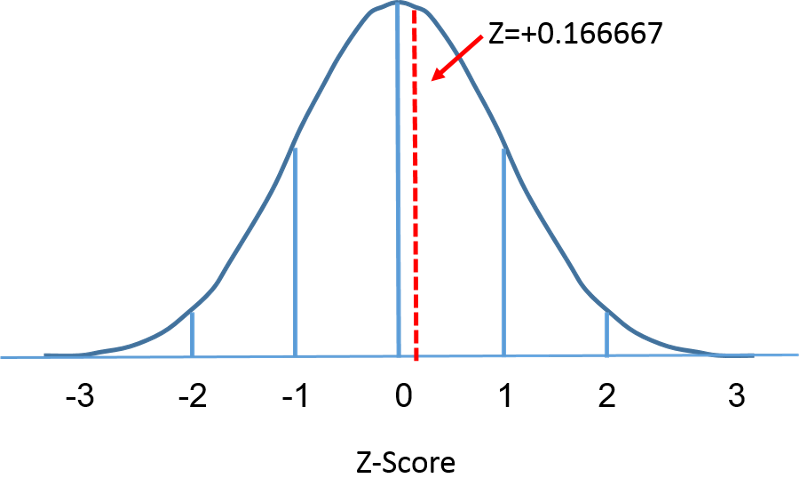
Distribuția normală standard este o distribuție normală cu media zero și abaterea standard de 1. Distribuția normală standard este centrată la zero, iar gradul în care o anumită măsurătoare se abate de la medie este dat de abaterea standard. În cazul distribuției normale standard, 68% dintre observații se situează în limita unei abateri standard de la medie; 95% se situează în limita a două abateri standard de la medie; și 99,9% se situează în limita a 3 abateri standard de la medie. Până în acest moment, am folosit „X” pentru a desemna variabila de interes (de exemplu, X=BMI, X=înălțime, X=greutate). Cu toate acestea, atunci când utilizăm o distribuție normală standard, vom folosi „Z” pentru a ne referi la o variabilă în contextul unei distribuții normale standard. După standarizare, IMC=30 discutat pe pagina anterioară este prezentat mai jos, aflându-se cu 0,16667 unități deasupra mediei de 0 pe distribuția normală standard din dreapta.
 ====
====
Din moment ce aria de sub curba standard = 1, putem începe să definim mai precis probabilitățile de observare specifică. Pentru orice scor Z dat, putem calcula aria de sub curba din stânga acelui scor Z. Tabelul din cadrul de mai jos prezintă probabilitățile pentru distribuția normală standard. Examinați tabelul și observați că un scor „Z” de 0,0 indică o probabilitate de 0,50 sau 50%, iar un scor „Z” de 1, adică o abatere standard peste medie, indică o probabilitate de 0,8413 sau 84%. Acest lucru se datorează faptului că o abatere standard deasupra și sub medie cuprinde aproximativ 68% din suprafață, astfel încât o abatere standard deasupra mediei reprezintă jumătate din aceasta, adică 34%. Deci, cei 50% sub medie plus cei 34% deasupra mediei ne dau 84%.
Probabilități ale distribuției normale standard Z
![]()
Acest tabel este organizat pentru a furniza aria de sub curbă la stânga sau mai mică decât o valoare specificată sau „valoarea Z”. În acest caz, deoarece media este zero și abaterea standard este 1, valoarea Z este numărul de unități de abatere standard de la medie, iar aria este probabilitatea de a observa o valoare mai mică decât acea valoare Z specifică. Observați, de asemenea, că tabelul arată probabilitățile cu două zecimale ale lui Z. Locul unităților și prima zecimală sunt afișate în coloana din stânga, iar a doua zecimală este afișată de-a lungul rândului de sus.
Dar să ne întoarcem la întrebarea despre probabilitatea ca IMC să fie mai mic de 30, adică P(X<30). Putem răspunde la această întrebare folosind distribuția normală standard. Figurile de mai jos arată distribuțiile IMC pentru bărbații în vârstă de 60 de ani și distribuția normală standard una lângă alta.
Distribuția IMC și distribuția normală standard
 ====
====
Aria de sub fiecare curbă este una, dar scalarea axei X este diferită. Observați, totuși, că suprafețele din stânga liniei punctate sunt aceleași. Distribuția BMI variază de la 11 la 47, în timp ce distribuția normală standardizată, Z, variază de la -3 la 3. Dorim să calculăm P(X < 30). Pentru a face acest lucru, putem determina valoarea Z care corespunde lui X = 30 și apoi să folosim tabelul distribuției normale standardizate de mai sus pentru a găsi probabilitatea sau aria de sub curbă. Următoarea formulă convertește o valoare X într-un scor Z, numit și scor standardizat:

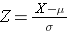
unde μ este media și σ este abaterea standard a variabilei X.
Pentru a calcula P(X < 30) convertim X=30 în scorul său Z corespunzător (acest lucru se numește standardizare):

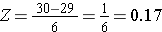
Așa, P(X < 30) = P(Z < 0,17). Putem apoi să căutăm probabilitatea corespunzătoare pentru acest scor Z din tabelul de distribuție normală standard, care arată că P(X < 30) = P(Z < 0,17) = 0,5675. Astfel, probabilitatea ca un bărbat în vârstă de 60 de ani să aibă un IMC mai mic de 30 este de 56,75%.
Un alt exemplu
Utilizând aceeași distribuție pentru IMC, care este probabilitatea ca un bărbat în vârstă de 60 de ani să aibă un IMC mai mare de 35? Cu alte cuvinte, care este P(X > 35)? Din nou standardizăm:

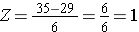
Acum mergem la tabelul distribuției normale standard pentru a căuta P(Z>1) și pentru Z=1,00 găsim că P(Z<1,00) = 0,8413. Observați, totuși, că tabelul oferă întotdeauna probabilitatea ca Z să fie mai mică decât valoarea specificată, adică ne dă P(Z<1)=0,8413.
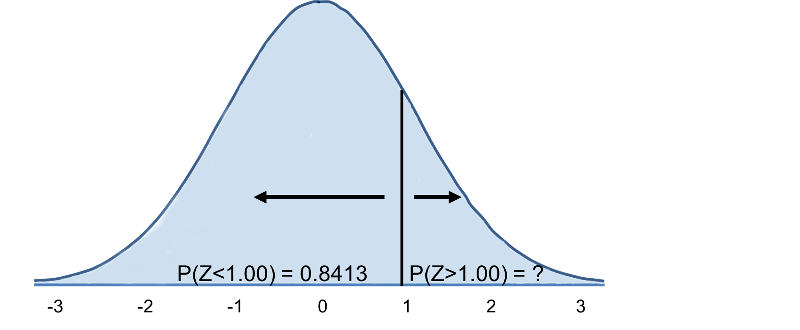
Din acest motiv, P(Z>1)=1-0,8413=0,1587. Interpretare: Aproape 16% dintre bărbații în vârstă de 60 de ani au un IMC peste 35.
Calculator de probabilități normale
![]()
![]()
Z-Scores with R
Ca alternativă la căutarea probabilităților normale în tabel sau la utilizarea Excel, putem utiliza R pentru a calcula probabilitățile. De exemplu,
> pnorm(0)
Un scor Z de 0 (media oricărei distribuții) are 50% din suprafața din stânga. Care este probabilitatea ca un bărbat de 60 de ani din populația de mai sus să aibă un IMC mai mic de 29 (media)? Scorul Z ar fi 0, iar pnorm(0)=0,5 sau 50%.
Care este probabilitatea ca un bărbat de 60 de ani să aibă un IMC mai mic de 30? Punctajul Z a fost de 0,16667.
> pnorm(0,16667)
Atunci, probabilitatea este de 56,6%.
Care este probabilitatea ca un bărbat de 60 de ani să aibă un IMC mai mare de 35?
35-29=6, ceea ce reprezintă o abatere standard peste medie. Deci putem calcula aria din stânga
> pnorm(1)
și apoi să scădem rezultatul din 1,0.
1-0,8413447= 0,1586553
Deci probabilitatea ca un bărbat în vârstă de 60 de ani să aibă un IMC mai mare de 35 este de 15,8%.
Sau putem folosi R pentru a calcula totul într-un singur pas, după cum urmează:
> 1-pnorm(1)
Probabilitate pentru un interval de valori

Care este probabilitatea ca un bărbat în vârstă de 60 de ani să aibă IMC între 30 și 35? Rețineți că acest lucru este același lucru cu a întreba ce proporție de bărbați în vârstă de 60 de ani au IMC între 30 și 35. Mai exact, dorim P(30 < X < 35)? Am calculat anterior P(30<X) și P(X<35); cum pot fi folosite aceste două rezultate pentru a calcula probabilitatea ca IMC să fie între 30 și 35? Încercați să formulați și să răspundeți pe cont propriu înainte de a vă uita la explicația de mai jos.
Răspuns
.