
Plantele pot crește noi celule în spirală, cum ar fi modelul de semințe din această frumoasă floarea-soarelui.
Spirala se produce în mod natural deoarece fiecare celulă nouă se formează după o întoarcere.
„O nouă celulă, apoi întoarcere,
apoi o altă celulă, apoi întoarcere, …”
Cât de departe să te întorci?
Deci, dacă ai fi o plantă, cât de mult te-ai întoarce între celulele noi?
Dacă nu te întorci deloc, obții o linie dreaptă.
![]()
Dar acesta este un design foarte slab …. vrei ceva rotund care să se țină împreună fără goluri.
De ce să nu încerci să găsești cea mai bună valoare pentru tine?
Încearcă diferite valori, cum ar fi 0,75, 0,9, 3,1416, 0,62, etc.
Amintește-ți, încerci să faci un model fără goluri de la început până la sfârșit:
(Apropo, nu contează partea cu numere întregi, cum ar fi 1. sau 5. pentru că sunt revoluții complete care ne îndreaptă înapoi în aceeași direcție.)
Ce ai obținut?
Dacă ai obținut ceva care se termină ca 0,618 (sau 0,382, care este 1 – 0,618) atunci „Felicitări, ești un membru de succes al regnului vegetal!”
 |
Aceasta pentru că Raportul de Aur (1.61803…) este cea mai bună soluție, iar Floarea-soarelui a descoperit acest lucru în felul său natural. Încercați… ar trebui să arate așa. |
De ce?
Care număr care este o fracție simplă (exemplu: 0.75 este 3/4, iar 0,95 este 19/20, etc.) va face, după un timp, un model de linii care se suprapun, ceea ce face goluri.
Dar Raportul de Aur (simbolul său este litera grecească Phi, prezentată în stânga) este expert în a nu fi nicio fracție.
Este un număr irațional (ceea ce înseamnă că nu îl putem scrie ca o fracție simplă), dar mai mult decât atât… este cât se poate de departe de a fi aproape de orice fracție.
| Să fie doar irațional nu este suficient | |
|---|---|
 |
Pi (3,141592654…), care este de asemenea irațional. Din păcate are o zecimală foarte apropiată de 1/7 (= 0,142857…), așa că se termină cu 7 brațe. |
 |
e (2,71828…), de asemenea irațională, nu funcționează nici ea, deoarece zecimala sa este apropiată de 5/7 (0,714285…), deci se termină tot cu 7 brațe. |
Deci, cum funcționează raportul de aur?
| Una dintre proprietățile speciale ale Proporției de Aur este că ea poate fi definită în termenii ei însăși, astfel: | |
| (În numere: 1,61803… = 1 + 1/1,61803…) | |
| Ceasta poate fi dezvoltată în această fracție care continuă la nesfârșit (numită „fracție continuă”): | |
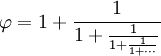 |
|
Așa, se strecoară frumos între fracțiile simple.
Numerele Fibonacci
Există o relație specială între Raportul de Aur și numerele Fibonacci (0, 1, 1, 1, 2, 3, 5, 8, 13, 21, … etc, fiecare număr este suma celor două numere dinaintea lui).
Când luăm oricare două numere Fibonacci succesive (unul după altul), raportul lor este foarte apropiat de Raportul de Aur:
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
2
|
3
|
1.5 | |
|
3
|
5
|
1.666666666… | |
|
5
|
8
|
1.6 | |
|
8
|
13
|
1.625 | |
|
13
|
21
|
1.615384615… | |
|
…
|
…
|
… | |
|
144
|
233
|
1.618055556… | |
|
233
|
377
|
1.618025751…. | |
|
…
|
…
|
… |

Așa că, la fel cum obținem în mod natural șapte brațe atunci când folosim 0.142857 (1/7), tindem să obținem numere Fibonacci atunci când folosim Raportul de Aur.
Încercați să numărați brațele spiralei – spiralele care „se întorc la stânga” și apoi spiralele care „se întorc la dreapta” … ce numere ați obținut?
Creșterea frunzelor în spirală

Acest comportament interesant nu se găsește doar în semințele de floarea-soarelui.
Frunzele, ramurile și petalele pot crește și ele în spirală.
De ce? Pentru ca frunzele noi să nu blocheze soarele de la frunzele mai bătrâne, sau pentru ca cantitatea maximă de ploaie sau rouă să fie dirijată spre rădăcini.
De fapt, atunci când o plantă are spirale, rotația tinde să fie o fracție realizată cu două numere Fibonacci succesive (una după alta), de exemplu:
- O jumătate de rotație este 1/2 (1 și 2 sunt numere Fibonacci)
- 3/5 este de asemenea comună (ambele numere Fibonacci), iar
- 5/8 de asemenea (ați ghicit!)
toate se apropie din ce în ce mai mult de Raportul de Aur.
|
Și acesta este motivul pentru care Numerele Fibonacci sunt foarte frecvente în plante. Iată o margaretă cu 21 de petale |
 |
Dar nu vedem acest lucru la toate plantele, deoarece natura are multe metode diferite de supraviețuire.
Unghiul de aur
Până acum am vorbit despre „întoarceri” (rotații complete).
Echivalentul a 0,61803… rotații este de 222,4922… grade, sau aproximativ 222,5°.
În cealaltă direcție este de aproximativ 137,5°, numit „Unghiul de Aur”.
Așa că, data viitoare când vă plimbați prin grădină, căutați Unghiul de Aur,
și numărați petalele și frunzele pentru a găsi Numerele Fibonacci,
și descoperiți cât de inteligente sunt plantele … !
Exercițiu
De ce nu mergeți chiar acum în grădină sau în parc și începeți să numărați frunzele și petalele și să măsurați rotațiile pentru a vedea ce găsiți.
Vă puteți scrie rezultatele pe acest formular:
| Numele sau descrierea plantei: | |||
| Frunzele cresc în spirale? Y / N | |||
| Numărați un grup de frunze: | |||
| Câte frunze (a) ? | |||
| Câte rotații complete (b) ? | |||
| Rotație pe frunză (b/a) : | |||
| Unghiul de rotație (360 × b/a) : | |||
| Există flori? Y / N | |||
| Câte petale are Floarea 1: | |||
| Floră 2: | |||
| Floră 3: | |||
(Dar nu uitați, natura are propriile reguli, și nu trebuie să urmeze modele matematice,
dar când o face este minunat de văzut.)
* Note despre animație
Semințele de floarea-soarelui cresc din centru spre exterior, dar pe animație mi s-a părut mai ușor să desenez mai întâi semințele mai tinere și să le adaug pe cele mai bătrâne.
Animația ar trebui să continue mai mult timp pentru a fi la fel ca floarea-soarelui – acest lucru ar rezulta în 55 de spirale în sensul acelor de ceasornic și 34 de spirale în sens invers acelor de ceasornic (numere Fibonacci succesive). Pur și simplu nu am vrut să dureze prea mult.
Spiralele nu sunt programate în ea – ele apar în mod natural ca urmare a încercării de a plasa semințele cât mai aproape una de alta, menținându-le în același timp la rotația corectă.
.

