Biografie
Johannes Kepler este astăzi amintit mai ales pentru descoperirea celor trei legi ale mișcării planetare care îi poartă numele, publicate în 1609 și 1619). De asemenea, a realizat lucrări importante în domeniul opticii (1604, 1611), a descoperit două noi poliedre regulate (1619), a oferit prima tratare matematică a împachetării strânse a sferelor egale (ceea ce a condus la o explicație a formei celulelor unui fagure de miere, 1611), a oferit prima dovadă a modului în care funcționează logaritmii (1624) și a conceput o metodă de găsire a volumelor solidelor de revoluție care (retrospectiv!) poate fi văzută ca o contribuție la dezvoltarea calculului (1615, 1616). Mai mult, el a calculat cele mai exacte tabele astronomice cunoscute până în prezent, a căror acuratețe continuă a contribuit în mare măsură la stabilirea adevărului astronomiei heliocentrice (Tabelele Rudolphine, Ulm, 1627).
Supraviețuiește o mare cantitate din corespondența lui Kepler. Multe dintre scrisorile sale sunt aproape echivalentul unei lucrări științifice (nu existau încă reviste științifice), iar corespondenții par să le fi păstrat pentru că erau interesante. În consecință, știm destul de multe despre viața lui Kepler și chiar despre caracterul său. În parte din această cauză, Kepler a avut o oarecare carieră ca personaj mai mult sau mai puțin fictiv (a se vedea nota istoriografică de mai jos).
Copilărie
Kepler s-a născut în orășelul Weil der Stadt din Suabia și s-a mutat cu părinții săi în apropiere, la Leonberg, în 1576. Tatăl său era un soldat mercenar, iar mama sa era fiica unui hangiu. Johannes a fost primul lor copil. Tatăl său a plecat de acasă pentru ultima oară când Johannes avea cinci ani și se crede că a murit în războiul din Țările de Jos. În copilărie, Kepler a locuit împreună cu mama sa în hanul bunicului său. El povestește că obișnuia să ajute, servind în han. Ne imaginăm că clienții erau uneori nedumeriți de competența neobișnuită a copilului la aritmetică.
Educația timpurie a lui Kepler a fost la o școală locală și apoi la un seminar din apropiere, de unde, cu intenția de a fi hirotonit, s-a înscris la Universitatea din Tübingen, pe atunci (ca și acum) un bastion al ortodoxiei luterane.
Opinile lui Kepler
De-a lungul vieții sale, Kepler a fost un om profund religios. Toate scrierile sale conțin numeroase referiri la Dumnezeu, iar el și-a văzut munca ca pe o împlinire a datoriei sale creștine de a înțelege lucrările lui Dumnezeu. Omul fiind, așa cum credea Kepler, făcut după chipul lui Dumnezeu, era în mod clar capabil să înțeleagă Universul pe care acesta îl crease. Mai mult, Kepler era convins că Dumnezeu a creat Universul conform unui plan matematic (o credință care se regăsește în operele lui Platon și este asociată cu Pitagora). Având în vedere că la acea vreme era general acceptat faptul că matematica oferea o metodă sigură de a ajunge la adevăruri despre lume (noțiunile și postulatele comune ale lui Euclid fiind considerate ca fiind adevărate), avem aici o strategie de înțelegere a Universului. Având în vedere că unii autori i-au atribuit lui Kepler un nume de iraționalitate, merită remarcat faptul că această epistemologie mai degrabă plină de speranță este într-adevăr foarte departe de convingerea misticului că lucrurile nu pot fi înțelese decât într-un mod imprecis, care se bazează pe intuiții care nu se supun rațiunii. Într-adevăr, Kepler îi mulțumește în mod repetat lui Dumnezeu pentru că i-a acordat intuiții, dar intuițiile sunt prezentate ca fiind raționale.
Educație universitară
În această perioadă, era obișnuit ca toți studenții unei universități să urmeze cursuri de „matematică”. În principiu, aceasta includea cele patru științe matematice: aritmetică, geometrie, astronomie și muzică. Se pare, totuși, că ceea ce se preda depindea depindea de universitatea respectivă. La Tübingen, Kepler a fost învățat astronomie de către unul dintre cei mai importanți astronomi ai vremii, Michael Mästlin (1550 – 1631). Astronomia din planul de învățământ era, bineînțeles, astronomia geocentrică, adică versiunea actuală a sistemului ptolemeic, în care toate cele șapte planete – Luna, Mercur, Venus, Soarele, Marte, Jupiter și Saturn – se mișcau în jurul Pământului, pozițiile lor față de stelele fixe fiind calculate prin combinarea mișcărilor circulare. Acest sistem era mai mult sau mai puțin în concordanță cu noțiunile actuale (aristotelice) de fizică, deși existau anumite dificultăți, cum ar fi dacă se putea considera „uniformă” (și, prin urmare, acceptabilă ca fiind evident eternă) o mișcare circulară care nu era uniformă în jurul propriului centru, ci în jurul unui alt punct (numit „ecuație”). Cu toate acestea, se pare că, în general, astronomii (care se vedeau pe ei înșiși ca „matematicieni”) erau mulțumiți să continue să calculeze pozițiile planetelor și să-i lase pe filosofii naturii să se preocupe dacă modelele matematice corespundeau sau nu mecanismelor fizice. Kepler nu a adoptat această atitudine. Prima sa lucrare publicată (1596) propune să se ia în considerare traiectoriile reale ale planetelor, nu cercurile folosite pentru a le construi.
La Tübingen, Kepler a studiat nu numai matematica, ci și greaca și ebraica (ambele necesare pentru a citi scripturile în limbile lor originale). Predarea se făcea în limba latină. La sfârșitul primului an, Kepler a obținut note de 10 la toate disciplinele, cu excepția matematicii. Probabil că Mästlin încerca să-i spună că se putea descurca mai bine, deoarece Kepler a fost, de fapt, unul dintre elevii selectați cărora a ales să le predea astronomie mai avansată, introducându-le noul sistem cosmologic heliocentric al lui Copernicus. De la Mästlin, Kepler a aflat că prefața la „Despre revoluții”, în care se explica faptul că aceasta era „doar matematică”, nu era scrisă de Copernic. Kepler pare să fi acceptat aproape instantaneu că sistemul copernican era adevărat din punct de vedere fizic; motivele pentru care l-a acceptat vor fi discutate în legătură cu primul său model cosmologic (vezi mai jos).
Se pare că încă din perioada studenției lui Kepler au existat indicii că convingerile sale religioase nu erau în totalitate în acord cu luteranismul ortodox curent la Tübingen și formulat în Confessio Augustana Ⓣ. Problemele lui Kepler cu această ortodoxie protestantă se refereau la presupusa relație dintre materie și „spirit” (o entitate nematerială) în doctrina Euharistiei. Acest lucru se leagă de astronomia lui Kepler în măsura în care se pare că acesta a întâmpinat dificultăți intelectuale oarecum similare în explicarea modului în care „forța” venită de la Soare ar putea afecta planetele. În scrierile sale, lui Kepler îi este dat să își expună opiniile pe șleau – ceea ce este foarte convenabil pentru istorici. În viața reală, pare probabil ca o tendință similară de deschidere să fi determinat autoritățile de la Tübingen să aibă îndoieli întemeiate cu privire la ortodoxia sa religioasă. Acestea ar putea explica de ce Mästlin l-a convins pe Kepler să renunțe la planurile de hirotonire și să accepte, în schimb, un post de profesor de matematică la Graz. Intoleranța religioasă s-a acutizat în anii următori. Kepler a fost excomunicat în 1612. Acest lucru i-a provocat multă suferință, dar, în ciuda statutului său social (pe atunci) relativ ridicat, ca matematician imperial, nu a reușit niciodată să obțină ridicarea interdicției.
Primul model cosmologic al lui Kepler (1596)
În loc de cele șapte planete din astronomia geocentrică standard, sistemul copernican avea doar șase, Luna devenind un corp de un tip necunoscut anterior astronomiei, pe care Kepler avea să îl numească mai târziu „satelit” (un nume pe care l-a inventat în 1610 pentru a descrie sateliții pe care Galileo descoperise că orbitau în jurul lui Jupiter, însemnând literal „însoțitor”). De ce șase planete?
În plus, în astronomia geocentrică nu exista nicio modalitate de a folosi observațiile pentru a afla dimensiunile relative ale sferelor planetare; se presupunea pur și simplu că acestea erau în contact. Acest lucru părea să nu necesite nicio explicație, deoarece se potrivea foarte bine cu credința filozofilor naturali că întregul sistem a fost girat de mișcarea celei mai îndepărtate sfere, una (sau poate două) dincolo de sfera stelelor „fixe” (cele al căror model formează constelațiile), dincolo de sfera lui Saturn. În sistemul copernican, faptul că componenta anuală a fiecărei mișcări planetare era o reflectare a mișcării anuale a Pământului permitea să se folosească observațiile pentru a calcula dimensiunea traiectoriei fiecărei planete și s-a dovedit că existau spații uriașe între planete. De ce aceste spații deosebite?
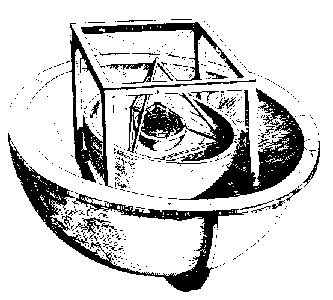
Răspunsul lui Kepler la aceste întrebări, descris în lucrarea sa Mysterium cosmographicum Ⓣ, Tübingen, 1596, pare bizar pentru cititorii secolului al XX-lea (vezi figura din dreapta). El a sugerat că, dacă o sferă ar fi trasată astfel încât să atingă interiorul traiectoriei lui Saturn, iar un cub ar fi înscris în sferă, atunci sfera înscrisă în acel cub ar fi sfera care circumscrie traiectoria lui Jupiter. Apoi, dacă un tetraedru regulat ar fi desenat în sfera care înscrie traiectoria lui Jupiter, sfera înscrisă în tetraedru ar fi sfera care circumscrie traiectoria lui Marte, și așa mai departe spre interior, plasând dodecaedrul regulat între Marte și Pământ, icosaedrul regulat între Pământ și Venus și octaedrul regulat între Venus și Mercur. Acest lucru explică perfect numărul de planete: există doar cinci solide regulate convexe (așa cum este demonstrat în Elemente de Euclid , cartea 13). De asemenea, oferă o potrivire convingătoare cu dimensiunile căilor deduse de Copernic, cea mai mare eroare fiind mai mică de 10% (ceea ce este spectaculos de bun pentru un model cosmologic chiar și acum). Kepler nu s-a exprimat în termeni de erori procentuale, iar al său este, de fapt, primul model cosmologic matematic, dar este ușor de înțeles de ce a crezut că dovezile observaționale îi susțin teoria.
Kepler a considerat că teoria sa cosmologică oferă dovezi pentru teoria copernicană. Înainte de a-și prezenta propria teorie, el a oferit argumente pentru a stabili plauzibilitatea teoriei copernicane în sine. Kepler afirma că avantajele sale față de teoria geocentrică constau în puterea sa explicativă mai mare. De exemplu, teoria copernicană poate explica de ce Venus și Mercur nu sunt niciodată văzute foarte departe de Soare (ele se află între Pământ și Soare), în timp ce în teoria geocentrică nu există nicio explicație pentru acest fapt. Kepler enumeră nouă astfel de întrebări în primul capitol din Mysterium cosmographicum Ⓣ.
Kepler a realizat această lucrare în timp ce preda la Graz, dar cartea a fost văzută prin presă la Tübingen de către Mästlin. Concordanța cu valorile deduse din observații nu era exactă, iar Kepler a sperat că observații mai bune vor îmbunătăți această concordanță, așa că a trimis o copie a Mysterium cosmographicum unuia dintre cei mai importanți astronomi observatori ai vremii, Tycho Brahe (1546 – 1601). Tycho, care lucra pe atunci la Praga (la acea vreme capitala Sfântului Imperiu Roman), îi scrisese de fapt deja lui Mästlin în căutarea unui asistent matematician. Kepler a primit postul.
„Războiul cu Marte”
În mod normal, prioritățile lui Tycho nu erau aceleași cu cele ale lui Kepler, iar Kepler s-a trezit curând lucrând la problema insolubilă a orbitei lui Marte . A continuat să lucreze la această problemă și după ce Tycho a murit (în 1601), iar Kepler i-a succedat ca matematician imperial. În mod convențional, orbitele erau compuse din cercuri și erau necesare destul de puține valori observaționale pentru a stabili razele și pozițiile relative ale cercurilor. Tycho făcuse un număr uriaș de observații, iar Kepler s-a hotărât să le utilizeze cât mai bine posibil. În esență, el a avut la dispoziție atât de multe observații încât, odată ce a construit o orbită posibilă, a putut să o verifice în funcție de alte observații până când s-a ajuns la un acord satisfăcător. Kepler a ajuns la concluzia că orbita lui Marte era o elipsă cu Soarele într-unul dintre focarele sale (un rezultat care, extins la toate planetele, se numește acum „Prima lege a lui Kepler”) și că o linie care unește planeta cu Soarele a măturat suprafețe egale în timpuri egale pe măsură ce planeta își descria orbita („A doua lege a lui Kepler”), adică suprafața este folosită ca măsură a timpului. După ce această lucrare a fost publicată în Astronomia nova, … Ⓣ, Heidelberg, 1609, Kepler a găsit orbite pentru celelalte planete, stabilind astfel că cele două legi sunt valabile și pentru ele. Ambele legi raportează mișcarea planetei la Soare; copernicanismul lui Kepler a fost crucial pentru raționamentul său și pentru deducțiile sale.
Procesul propriu-zis de calcul pentru Marte a fost extrem de laborios – există aproape o mie de foi de aritmetică în folio care au supraviețuit – și Kepler însuși se referă la această lucrare ca la „războiul meu cu Marte”, dar rezultatul a fost o orbită care concordă cu rezultatele moderne atât de exact încât comparația trebuie să țină cont de schimbările seculare ale orbitei de pe vremea lui Kepler.
Eroare de observație
A fost crucial pentru metoda lui Kepler de verificare a orbitelor posibile în raport cu observațiile, ca el să aibă o idee despre ceea ce ar trebui să fie acceptat ca fiind un acord adecvat. De aici rezultă prima utilizare explicită a conceptului de eroare observațională. Este posibil ca Kepler să fi datorat această noțiune, cel puțin parțial, lui Tycho, care făcea verificări detaliate ale performanțelor instrumentelor sale (a se vedea biografia lui Brahe).
Optica și noua stea din 1604
Lucrarea despre Marte a fost în esență finalizată în 1605, dar au existat întârzieri în publicarea cărții. Între timp, ca răspuns la preocupările legate de diametrul aparent diferit al Lunii atunci când este observată direct și atunci când este observată cu ajutorul unei camere obscure, Kepler a lucrat la optică și a prezentat prima teorie matematică corectă a camerei obscure și prima explicație corectă a funcționării ochiului uman, cu o imagine inversă formată pe retină. Aceste rezultate au fost publicate în Ad Vitellionem paralipomena, quibus astronomiae pars optica traditur Ⓣ, Frankfurt, 1604. El a scris, de asemenea, despre steaua nouă din 1604, numită acum de obicei „supernova lui Kepler”, respingând numeroase explicații și remarcând la un moment dat că, desigur, această stea ar putea fi doar o creație specială „dar înainte de a ajunge la cred că ar trebui să încercăm orice altceva” De stella nova Ⓣ, Praga, 1606, capitolul 22, KGW 1, p. 257, linia 23.
În urma utilizării telescopului de către Galileo în descoperirea sateliților lui Jupiter, publicată în lucrarea sa Sidereal Messenger (Veneția, 1610), la care Kepler a scris un răspuns entuziast (1610), Kepler a scris un studiu al proprietăților lentilelor (prima lucrare de acest fel despre optică) în care a prezentat un nou model de telescop, folosind două lentile convexe (Dioptrice, Praga, 1611). Acest design, în care imaginea finală este inversată, a avut un succes atât de mare încât acum este cunoscut de obicei nu ca telescop keplerian, ci pur și simplu ca telescop astronomic.
Plecarea de la Praga pentru Linz
Anii petrecuți de Kepler la Praga au fost relativ pașnici și extrem de productivi din punct de vedere științific. De fapt, chiar și atunci când lucrurile au mers prost, se pare că nu a permis niciodată ca circumstanțele externe să îl împiedice să își continue munca. Lucrurile au început să meargă foarte prost la sfârșitul anului 1611. Mai întâi, fiul său de șapte ani a murit. Kepler i-a scris unui prieten că această moarte a fost deosebit de greu de suportat, deoarece copilul îi amintea atât de mult de el însuși la acea vârstă. Apoi, soția lui Kepler a murit. Apoi, împăratul Rudolf, a cărui sănătate era șubredă, a fost forțat să abdice în favoarea fratelui său Matei, care, ca și Rudolf, era catolic, dar (spre deosebire de Rudolf) nu credea în toleranța față de protestanți. Kepler a fost nevoit să părăsească Praga. Înainte de a pleca, a dispus ca trupul soției sale să fie mutat în mormântul fiului său și a scris un epitaf în latină pentru ei. El și copiii rămași s-au mutat la Linz (acum în Austria).
Căsătorie și butoaie de vin
Kepler pare să se fi căsătorit cu prima sa soție, Barbara, din dragoste (deși căsătoria a fost aranjată prin intermediul unui broker). Cea de-a doua căsătorie, în 1613, a fost o chestiune de necesitate practică; avea nevoie de cineva care să aibă grijă de copii. Noua soție a lui Kepler, Susanna, a avut parte de un curs intensiv de cunoaștere a caracterului lui Kepler: în scrisoarea dedicatorie la cartea rezultată se explică faptul că, la festivitățile de nuntă, a observat că volumele butoaielor de vin erau estimate cu ajutorul unei tije strecurate în diagonală prin gaura de bungă și a început să se întrebe cum ar putea funcționa așa ceva. Rezultatul a fost un studiu al volumelor solidelor de revoluție Nova stereometria doliorum … Ⓣ, Linz, 1615, în care Kepler, bazându-se pe lucrările lui Arhimede, a folosit o rezolvare în „indivizibile”. Această metodă a fost dezvoltată mai târziu de Bonaventura Cavalieri (c. 1598 – 1647) și face parte din strămoșii calculului infinitezimal.
Armonia lumii
Principala sarcină a lui Kepler în calitate de matematician imperial a fost aceea de a scrie tabele astronomice, pe baza observațiilor lui Tycho, dar ceea ce dorea cu adevărat să facă era să scrie Armonia lumii, planificată încă din 1599 ca o dezvoltare a Misterului Cosmosului său. Această a doua lucrare despre cosmologie (Harmonices mundi libri V Ⓣ, Linz, 1619) prezintă un model matematic mai elaborat decât cel anterior, deși poliedrele sunt tot acolo. Matematica din această lucrare include prima tratare sistematică a teselațiilor, o demonstrație că există doar treisprezece poliedre uniforme convexe (solidele arhimediene) și prima prezentare a două poliedre regulate neconvexe (toate în Cartea 2). Armonia lumii conține, de asemenea, ceea ce astăzi este cunoscut sub numele de „a treia lege a lui Kepler”, conform căreia, pentru oricare două planete, raportul dintre pătratele perioadelor lor va fi același cu raportul dintre cuburile razelor medii ale orbitelor lor. Încă de la prima, Kepler a căutat o regulă care să stabilească o relație între dimensiunile orbitelor și perioadele lor, dar nu a existat o serie de pași lenți către această lege, așa cum a fost cazul celorlalte două. De fapt, deși cea de-a treia lege joacă un rol important în unele dintre secțiunile finale ale versiunii tipărite a Armoniei lumii, ea nu a fost descoperită până când lucrarea nu a fost tipărită. Kepler a făcut revizuiri de ultim moment. El însuși povestește povestea succesului final:
…și dacă vreți momentul exact în timp, ea a fost concepută mental la 8 martie în acest an o mie șase sute optsprezece, dar supusă calculului într-un mod nefericit și, prin urmare, respinsă ca fiind falsă și, în cele din urmă, revenind la 15 mai și adoptând o nouă linie de atac, a luat cu asalt întunericul minții mele. Atât de puternic a fost sprijinul oferit de combinația dintre munca mea de șaptesprezece ani asupra observațiilor lui Brahe și studiul de față, care conspirau împreună, încât la început am crezut că visez și că îmi asum concluzia printre premisele mele de bază. Dar este absolut sigur și exact că „proporția dintre timpii periodici ai oricăror două planete este exact proporția sesquialterată a distanțelor lor medii…”
(Harmonice mundi Cartea 5, Capitolul 3, trad. Aiton, Duncan și Field, p. 411).
Proces de vrăjitorie
În timp ce Kepler lucra la lucrarea sa Armonia lumii, mama sa a fost acuzată de vrăjitorie. El a apelat la ajutorul facultății de drept de la Tübingen. Katharina Kepler a fost în cele din urmă eliberată, cel puțin parțial ca urmare a obiecțiilor tehnice rezultate din nerespectarea de către autorități a procedurilor legale corecte în utilizarea torturii. Documentele care au supraviețuit sunt înfiorătoare. Cu toate acestea, Kepler a continuat să lucreze. În trăsură, în călătoria sa spre Württemberg pentru a-și apăra mama, a citit o lucrare despre teoria muzicii a lui Vincenzo Galilei (c.1520 – 1591, tatăl lui Galileo), la care există numeroase referințe în Armonia lumii.
Tabele astronomice
Calcularea tabelelor, activitatea normală pentru un astronom, a implicat întotdeauna o aritmetică grea. În consecință, Kepler a fost încântat când, în 1616, a dat peste lucrarea lui Napier despre logaritmi (publicată în 1614). Cu toate acestea, Mästlin i-a spus cu promptitudine, în primul rând, că era nepotrivit ca un matematician serios să se bucure de un simplu ajutor pentru calcul și, în al doilea rând, că nu era înțelept să aibă încredere în logaritmi, deoarece nimeni nu înțelegea cum funcționează aceștia. (Comentarii similare au fost făcute despre calculatoare la începutul anilor 1960.) Răspunsul lui Kepler la cea de-a doua obiecție a fost să publice o demonstrație a modului în care funcționau logaritmii, bazată pe o sursă impecabil de respectabilă: Cartea 5 a Elementelor lui Euclid. Kepler a calculat tabele de logaritmi cu opt cifre, care au fost publicate împreună cu Tabelele Rudolphine (Ulm, 1628). Tabelele astronomice au folosit nu numai observațiile lui Tycho, ci și primele două legi ale lui Kepler. Toate tabelele astronomice care s-au folosit de noile observații au fost exacte în primii câțiva ani de la publicare. Ceea ce a fost remarcabil la Tabelele Rudolphine a fost faptul că acestea s-au dovedit a fi exacte de-a lungul deceniilor. Și, pe măsură ce anii se adunau, precizia continuă a tabelelor a fost, în mod natural, văzută ca un argument în favoarea corectitudinii legilor lui Kepler și, prin urmare, a corectitudinii astronomiei heliocentrice. Îndeplinirea de către Kepler a sarcinii sale oficiale plictisitoare de matematician imperial a dus la împlinirea celei mai dragi dorințe a sa, aceea de a contribui la stabilirea copernicanismului.
Wallenstein
În momentul publicării Tablourilor Rudolfine, Kepler nu mai lucra, de fapt, pentru împărat (părăsise Linz în 1626), ci pentru Albrecht von Wallenstein (1583 – 1632), unul dintre puținii conducători militari de succes în Războiul de Treizeci de Ani (1618 – 1648).
Wallenstein, ca și împăratul Rudolf, se aștepta ca Kepler să îi dea sfaturi bazate pe astrologie. În mod firesc, Kepler a trebuit să se supună, dar subliniază în mod repetat că nu crede că se pot face predicții precise. La fel ca majoritatea oamenilor din acea vreme, Kepler a acceptat principiul astrologiei, conform căruia corpurile cerești ar putea influența ceea ce se întâmplă pe Pământ (cele mai clare exemple fiind Soarele care provoacă anotimpurile și Luna mareele), dar, în calitate de copernican, nu a crezut în realitatea fizică a constelațiilor. Astrologia sa se baza doar pe unghiurile dintre pozițiile corpurilor cerești („aspecte astrologice”). El își exprimă un dispreț total față de sistemele complicate ale astrologiei convenționale.
Moarte
Kepler a murit la Regensburg, după o scurtă boală. El se afla în oraș în drum spre a încasa niște bani care i se datorau în legătură cu Tabelele Rudolphine. A fost înmormântat în biserica locală, dar aceasta a fost distrusă în cursul Războiului de Treizeci de Ani și nu a mai rămas nimic din mormânt.
Nota istoriografică
S-au făcut uneori multe referiri la presupusele elemente non-raționale din activitatea științifică a lui Kepler. Astrologii credincioși pretind frecvent că lucrările sale oferă un antecedent respectabil din punct de vedere științific pentru ale lor. În influentul său volum Sleepwalkers, regretatul Arthur Koestler a făcut din lupta lui Kepler cu Marte un argument pentru iraționalitatea inerentă a științei moderne. Au existat mulți adepți tacitali ai acestor două convingeri. Ambele se bazează, însă, pe o lectură foarte parțială a operei lui Kepler. În special, Koestler pare să nu fi avut expertiza matematică necesară pentru a înțelege procedurile lui Kepler. Un studiu mai atent arată că Koestler s-a înșelat pur și simplu în evaluarea sa.
Elementul non-rațional cu adevărat important din opera lui Kepler este creștinismul său. Utilizarea extensivă și reușită a matematicii de către Kepler face ca opera sa să pară „modernă”, dar de fapt avem de-a face cu un filosof naturalist creștin, pentru care înțelegerea naturii Universului includea înțelegerea naturii Creatorului său.