Care sunt frecvențele notelor muzicale?

În tabelul de frecvențe de mai jos, veți găsi A = 440 Hz, apoi

A# = 466,16 Hz,
B = 493,88 Hz,
C = 523,25 Hz, etc.

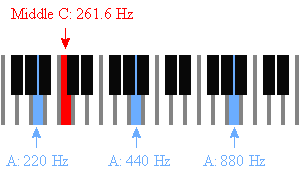
De asemenea, puteți găsi Do mijlociu: 261.63 Hz.

Acestea se găsesc folosind

frecvența `= 440×2^(n”/”12)`

pentru `n = -21, -19, …., 27`

De unde provine această formulă?

Această problemă mi-a amintit de dobânda compusă pe care am întâlnit-o mai devreme la Money Math. Frecvența trebuie să se dubleze la fiecare `12` note (pentru că există `7` note albe și `5` note negre în fiecare octavă.)

Iată un grafic al acestei relații:

frecvența `= 440×2^(n”/”12)`

Este o curbă exponențială, pe care am întâlnit-o mai devreme la Grafice de funcții exponențiale.

Acordare cu temperament egal

O problemă interesantă se confruntă constructorii de instrumente muzicale de sute de ani. Pentru a obține o „5-a perfectă” (intervalul dintre La și Mi de mai sus, să zicem), trebuie să cântăm o notă care să aibă `1,5` ori frecvența lui La.

La o vioară (sau la o violă sau la orice instrument cu coarde fără frison) acest lucru este posibil, și putem cânta un Mi perfect și frumos la `440 × 1,5 = 660 „Hz”`. Dar observați (din tabelul de frecvențe de mai sus) că un pian care cântă aceeași notă va cânta Mi `= 659,26\”Hz”` .

Cu aproximativ 400 de ani în urmă, clapele (de obicei clavecine și orgi) erau acordate pentru un anumit grup de clape, astfel încât toate instrumentele, în special cele cu coarde, să sune „corect” în acele clape. Clavecinul suna grozav în acele clape, dar destul de groaznic în alte clape fără legătură între ele (să zicem B bemol).

Existau, de fapt, mai multe sisteme de acordaj diferite folosite în timpul lui Bach, printre care meantone (care urmărea să facă să sune bine în 3rde majore, dar nu era la fel de preocupat de calitatea cvintei majore, cu efectul că unele clape nu erau utilizabile), și acordajul lui Werckmeister din 1691, care permitea compozitorilor să creeze muzică în orice cheie (cu efectul că diferitele chei aveau o calitate tonală diferită).

La începutul secolului al XX-lea, s-a decis acordarea clapelor astfel încât notele să fie distanțate în mod egal (ca frecvențele date în tabelul prezentat mai sus). Acest lucru se numește acordaj temperat egal. O astfel de acordaj era cunoscut pe vremea lui Bach, dar a fost respins deoarece era considerat prea „fad” (toate clapele au aceeași calitate a sunetului) și nu existau instrumente de măsurare a frecvențelor care ar fi permis acordaje exacte.

Din păcate, acordajul temperat egal înseamnă că toate instrumentele cu coarde trebuie să țină cont de ușoarele diferențe de acordaj dintre instrumente atunci când sunt implicate și clapele. De obicei, corzile sunt cele mai fericite atunci când cântă doar cu alte corzi, din acest motiv.