Selecção – Algoritmo, Código Fonte, Complexidade temporal

Este artigo faz parte da série “Algoritmos de Selecção”: Ultimate Guide” e…

• descreve como Selection Sort funciona,
• inclui o código fonte Java para Selection Sort,
• mostra como derivar a sua complexidade temporal (sem matemática complicada)
• e verifica se a performance da implementação Java corresponde ao comportamento esperado em tempo de execução.

Você pode encontrar o código fonte para toda a série de artigos no meu repositório GitHub.

Exemplo: Classificando Cartas de Jogo

Classificar cartas de jogo na mão é o exemplo clássico para o Insertion Sort.

Selection Sort também pode ser ilustrado com cartas de jogo. Não conheço ninguém que pegue suas cartas desta maneira, mas como exemplo, funciona muito bem 😉

Primeiro, você coloca todas as suas cartas de face para cima na mesa na sua frente. Procura a carta mais pequena e leva-a para a esquerda da sua mão. Depois procura a próxima carta maior e coloca-a à direita da carta mais pequena, e assim sucessivamente até que finalmente pegue na carta maior à extrema direita.

Diferença para o Insert Sort

Com o Insert Sort, pegamos na próxima carta não ordenada e inserimo-la na posição correcta nas cartas ordenadas.

Selection Sort funciona ao contrário: Selecionamos o menor cartão dos cartões não ordenados e então – um após o outro – anexamos aos cartões já ordenados.

Selection Sort Algorithm

O algoritmo pode ser explicado de forma mais simples por um exemplo. Nos passos seguintes, eu mostro como ordenar o array com Selection Sort:

Step 1

Dividimos o array em uma parte à esquerda, ordenada, e uma parte à direita, não ordenada. A parte ordenada é vazia no início:

Passo 2

Procuramos o menor elemento à direita, parte não ordenada. Para isso, primeiro lembramos o primeiro elemento, que é o 6. Vamos para o campo seguinte, onde encontramos um elemento ainda menor no 2. Caminhamos sobre o resto do array, procurando por um elemento ainda menor. Como não conseguimos encontrar um, ficamos com o 2. Colocamo-lo na posição correcta, trocando-o com o elemento em primeiro lugar. Depois movemos a borda entre as seções do array um campo para a direita:

Passo 3

Procuramos novamente na parte direita, não classificada, o elemento menor. Desta vez é o 3; trocamos com o elemento na segunda posição:

Passo 4

Ganho procuramos o elemento mais pequeno na secção da direita. É o 4, que já se encontra na posição correcta. Portanto não há necessidade de operação de troca neste passo, e nós apenas movemos a borda da seção:

Passo 5

Como o menor elemento, encontramos o 6. Trocamo-lo com o elemento no início da parte direita, o 9:

Passo 6

Dos dois elementos restantes, o 7 é o menor. Nós trocamos com o 9:

Algoritmo Acabado

O último elemento é automaticamente o maior e, portanto, na posição correta. O algoritmo está terminado, e os elementos são ordenados:

Selection Sort Java Source Code

Nesta seção, você encontrará uma implementação Java simples de Selection Sort.

O loop externo itera sobre os elementos a serem ordenados, e termina após o penúltimo elemento. Quando este elemento é ordenado, o último elemento é automaticamente ordenado também. A variável de laço i aponta sempre para o primeiro elemento da direita, parte não ordenada.

Em cada ciclo de laço, o primeiro elemento da parte direita é inicialmente assumido como o menor elemento min; sua posição é armazenada em minPos.

O loop interno então itera do segundo elemento da parte direita para o seu fim e reatribui min e minPos sempre que um elemento ainda menor for encontrado.

Após o loop interno ter sido completado, os elementos das posições i (início da parte direita) e minPos são trocados (a menos que sejam o mesmo elemento).

public class SelectionSort { public static void sort(int elements) { int length = elements.length; for (int i = 0; i < length - 1; i++) { // Search the smallest element in the remaining array int minPos = i; int min = elements; for (int j = i + 1; j < length; j++) { if (elements < min) { minPos = j; min = elements; } } // Swap min with element at pos i if (minPos != i) { elements = elements; elements = min; } } }}

O código mostrado difere da classe SelectionSort no repositório GitHub por implementar a interface SortAlgorithm para ser facilmente intercambiável dentro do framework de teste.

Selection Sort Time Complexity

Denotamos com n o número de elementos, no nosso exemplo n = 6.

Os dois loops aninhados são uma indicação de que estamos lidando com uma complexidade de tempo* de O(n²). Este será o caso se ambos os loops iteram para um valor que aumenta linearmente com n.

É obviamente o caso do loop externo: ele conta até n-1.

E o laço interno?

Vejam a seguinte ilustração:

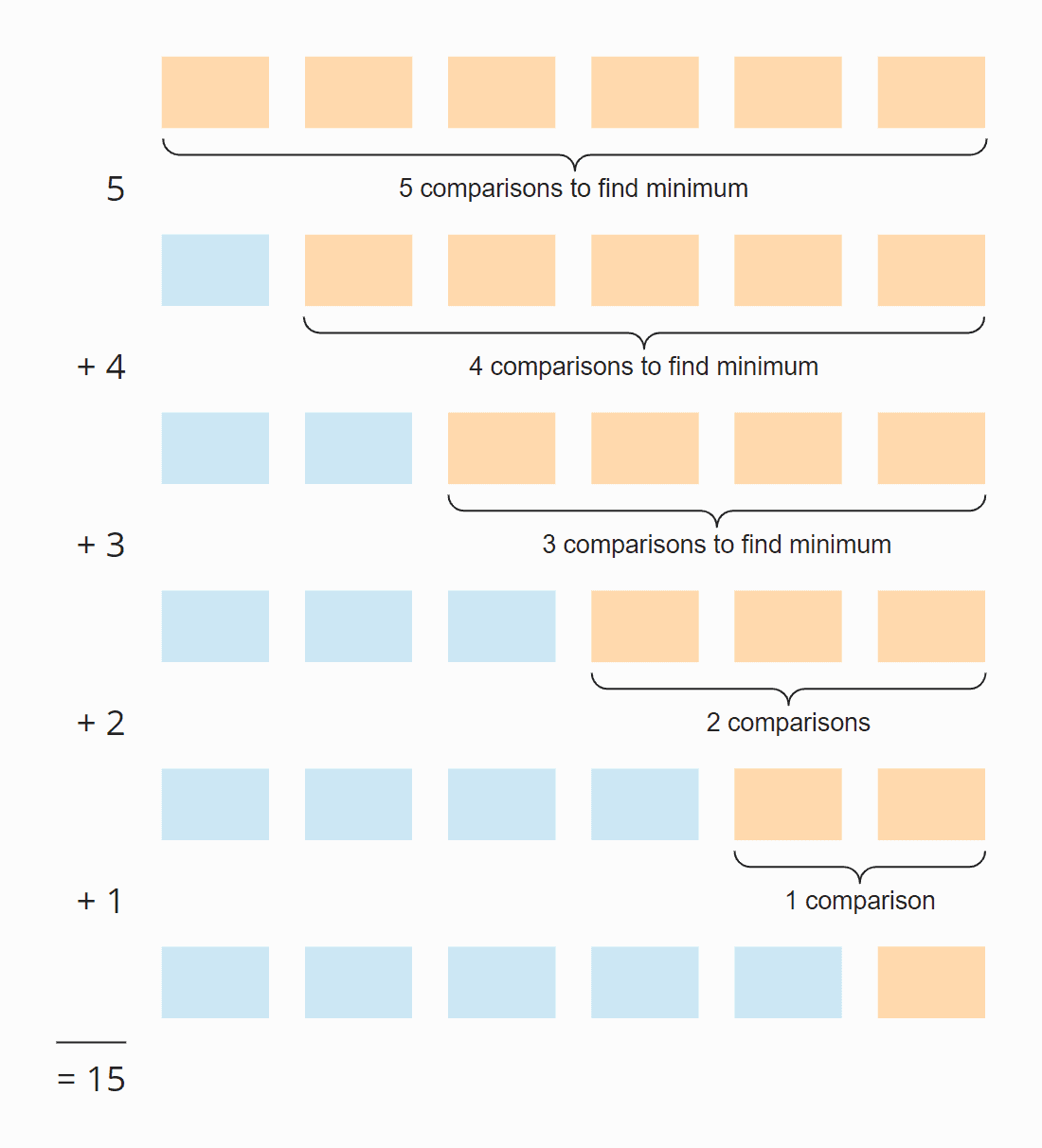
Em cada passo, o número de comparações é um a menos do que o número de elementos não seleccionados. No total, existem 15 comparações – independentemente de o array estar ou não inicialmente ordenado.

Isso também pode ser calculado da seguinte forma:

Seis elementos vezes cinco passos; divididos por dois, já que, em média, em todos os passos, metade dos elementos ainda estão não ordenados:

6 × 5 × ½ = 30 × ½ = 15

Se substituirmos 6 por n, obtemos

n × (n – 1) × ½

Quando multiplicado, isto é:

½ n² – ½ n

A potência mais alta de n neste termo é n². A complexidade de tempo para procurar o menor elemento é, portanto, O(n²) – também chamado “tempo quadrático”.

Vejamos agora a troca dos elementos. Em cada etapa (exceto a última), ou um elemento é trocado ou nenhum, dependendo se o menor elemento já está na posição correta ou não. Assim, temos, em suma, um máximo de n-1 operações de swapping, ou seja, a complexidade temporal de O(n) – também chamada “tempo linear”.

Para a complexidade total, apenas a classe de maior complexidade importa, portanto:

A complexidade temporal média, melhor e pior caso de Selection Sort é: O(n²)

* Os termos “complexidade temporal” e “O-notação” são explicados neste artigo usando exemplos e diagramas.

Tempo de execução do Exemplo de Ordenação de Seleção Java

Suficiente teoria! Eu escrevi um programa de teste que mede o tempo de execução do Selection Sort (e todos os outros algoritmos de ordenação cobertos nesta série) da seguinte forma:

• O número de elementos a serem ordenados duplica após cada iteração de 1.024 elementos inicialmente até 536.870.912 (= 229) elementos. Um array duas vezes este tamanho não pode ser criado em Java.
• Se um teste leva mais de 20 segundos, o array não é estendido mais.
• Todos os testes são executados com elementos não ordenados, bem como com elementos pré-ordenados ascendentes e descendentes.
• Permitimos que o compilador HotSpot otimize o código com duas rodadas de aquecimento. Depois disso, os testes são repetidos até que o processo seja abortado.

Após cada iteração, o programa imprime a mediana de todos os resultados das medições anteriores.

Aqui está o resultado para a Seleção Ordenar após 50 iterações (por uma questão de clareza, este é apenas um trecho; o resultado completo pode ser encontrado aqui):

n	unsorted	ascending	descending
…	…	…	…
16.384	27,9 ms	26,8 ms	65,6 ms
32.768	108,0 ms	105,4 ms	265,4 ms
65.536	434,0 ms	424,3 ms	1.052,2 ms
131,072	1.729,8 ms	1.714,1 ms	4.209,9 ms
262.144	6.913,4 ms	6.880,2 ms	16.863,7 ms
524.288	27.649,8 ms	27.568,7 ms	67.537,8 ms

Aqui as medidas mais uma vez como um diagrama (onde eu tenho mostrado “unsorted” e “ascendente” como uma curva devido aos valores quase idênticos):

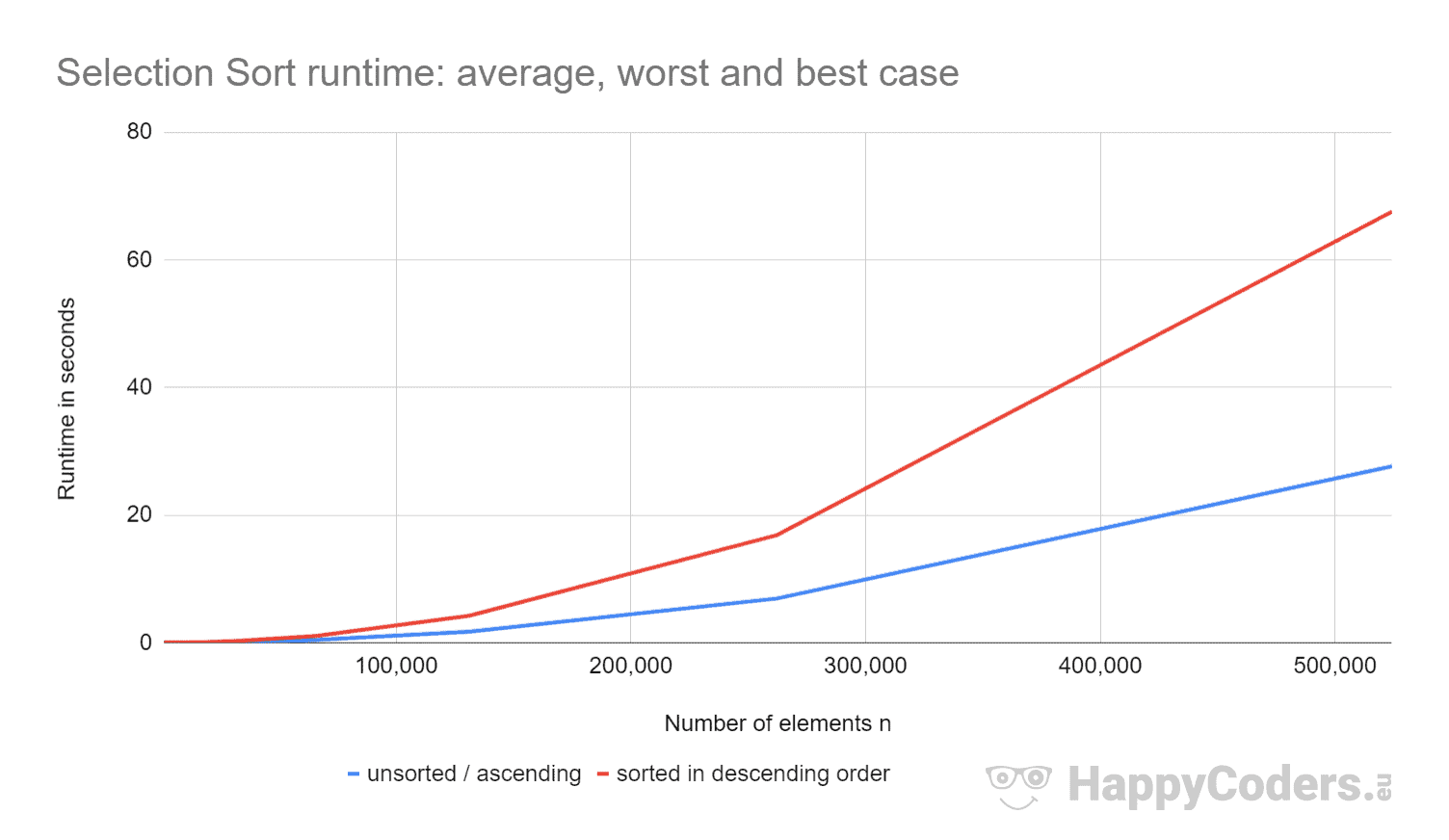
É bom ver que

• se o número de elementos for duplicado, o tempo de execução é aproximadamente quadruplicado – independentemente de os elementos estarem ou não previamente ordenados. Isto corresponde à complexidade de tempo esperada de O(n²).
• que o tempo de execução para elementos ordenados ascendentes é ligeiramente melhor do que para elementos não ordenados. Isto porque as operações de troca, que – como analisado acima – são de pouca importância, não são necessárias aqui.
• que o tempo de execução para elementos descendentes ordenados é significativamente pior do que para elementos não ordenados.

Por que é que?

Análise do tempo de execução do pior caso

Teoricamente, a busca pelo menor elemento deve sempre levar a mesma quantidade de tempo, independentemente da situação inicial. E as operações de swap devem ser apenas um pouco mais para elementos ordenados em ordem decrescente (para elementos ordenados em ordem decrescente, cada elemento teria que ser trocado; para elementos não ordenados, quase todos os elementos teriam que ser trocados).

Usando o programa CountOperations do meu repositório GitHub, podemos ver o número de várias operações. Aqui estão os resultados para elementos não ordenados e elementos ordenados em ordem decrescente, resumidos em uma tabela:

n	Comparações	Swaps unsorted	Swaps descendente	minPos/min unsorted	minPos/min descendente
…	…	…	…	…	…
512	130.816	504	256	2.866	66.047
1.024	523.776	1.017	512	6.439	263.167
2.048	2.096.128	2.042	1.024	14.727	1.050.623
4.096	8.386.560	4.084	2.048	30.758	4.198.399
8.192	33.550.336	8.181	4.096	69.378	16.785.407

Dos valores medidos pode-se ver:

• Com elementos ordenados em ordem decrescente, temos – como esperado – tantas operações de comparação como com elementos não ordenados – ou seja, n × (n-1) / 2.
• Com elementos não ordenados, temos – como assumido – quase tantas operações de swap como elementos: por exemplo, com 4.096 elementos não ordenados, há 4.084 operações de swap. Estes números mudam aleatoriamente de teste para teste.
• No entanto, com elementos ordenados em ordem decrescente, nós temos apenas metade das operações de swap como elementos! Isto porque, ao fazer swap, não só colocamos o menor elemento no lugar certo, mas também o respectivo parceiro de swap.

Com oito elementos, por exemplo, temos quatro operações de swap. Nas primeiras quatro iterações, temos uma cada e nas iterações cinco a oito, nenhuma (no entanto o algoritmo continua a correr até ao fim):

Outras, podemos ler a partir das medidas:

• O motivo pelo qual a ordenação de selecção é muito mais lenta com elementos ordenados em ordem decrescente pode ser encontrado no número de atribuições de variáveis locais (minPos e min) quando se procura o elemento mais pequeno. Enquanto com 8.192 elementos não ordenados, temos 69.378 dessas atribuições, com elementos ordenados em ordem decrescente, há 16.785.407 dessas atribuições – isso é 242 vezes mais!

Por que essa enorme diferença?

Análise do Tempo de Execução da Busca pelo Elemento Menor

Para elementos ordenados em ordem decrescente, a ordem de magnitude pode ser derivada da ilustração logo acima. A busca pelo elemento menor é limitada ao triângulo das caixas laranja e laranja-azul. Na parte superior alaranjada, os números em cada caixa se tornam menores; na parte direita alaranja-azul, os números aumentam novamente.

As operações de atribuição ocorrem em cada caixa laranja e na primeira das caixas laranja-azul. O número de operações de atribuição para minPos e min é assim, figurativamente falando, cerca de “um quarto do quadrado” – matematicamente e precisamente, é ¼ n² + n – 1.

Para elementos não classificados, teríamos de penetrar muito mais profundamente na matéria. Isso não só iria além do escopo deste artigo, mas de todo o blog.

Por isso, eu limito minha análise a um pequeno programa demonstrativo que mede quantos minPos/min atribuídos existem quando se procura o menor elemento em um array não ordenado. Aqui estão os valores médios após 100 iterações (um pequeno trecho; os resultados completos podem ser encontrados aqui):

n	número médio de atribuições de minPos/min024	7.08
4.096	8.61
16.385	8.94
65.536	11.81
262.144	12.22
1.048.576	14.26
4.194.304	14.71
16.777.216	16.44
67.108.864	17.92
268.435.456	20.27

Aqui como um diagrama com eixo x logarítmico:

O gráfico mostra muito bem que temos crescimento logarítmico, ou seja com cada duplicação do número de elementos, o número de atribuições aumenta apenas por um valor constante. Como eu disse, não vou me aprofundar em fundos matemáticos.

Esta é a razão pela qual estas minPos/min atribuições são de pouca importância em arrays não ordenados.

Outras Características de Seleção de Ordenação

Nas seções seguintes, discutirei a complexidade espacial, estabilidade e paralelismo da Seleção de Ordenação.

Complexidade espacial do Selection Sort

A complexidade espacial do Selection Sort é constante uma vez que não precisamos de espaço de memória adicional além das variáveis de loop i e j e as variáveis auxiliares length, minPos, e min.

Isto é, não importa quantos elementos ordenemos – dez ou dez milhões – só precisamos dessas cinco variáveis adicionais. Observamos o tempo constante como O(1).

Estabilidade da seleção de classificação

Selection Sort parece estável à primeira vista: Se a parte não ordenada contém vários elementos com a mesma chave, a primeira deve ser anexada à parte ordenada primeiro.

Mas as aparências são enganosas. Porque ao trocar dois elementos no segundo sub-passo do algoritmo, pode acontecer que certos elementos na parte não ordenada não tenham mais a ordem original. Isto, por sua vez, leva ao fato de que eles não aparecem mais na ordem original na seção ordenada.

Um exemplo pode ser construído de forma muito simples. Suponha que temos dois elementos diferentes com a chave 2 e um com a chave 1, dispostos da seguinte forma, e depois ordená-los com Selection Sort:

No primeiro passo, o primeiro e o último elemento são trocados. Assim o elemento “TWO” termina atrás do elemento “dois” – a ordem dos dois elementos é trocada.

No segundo passo, o algoritmo compara os dois elementos traseiros. Ambos têm a mesma chave, 2. Assim nenhum elemento é trocado.

No terceiro passo, resta apenas um elemento; este é automaticamente considerado ordenado.

Os dois elementos com a chave 2 foram assim trocados para a sua ordem inicial – o algoritmo é instável.

Variante estável da ordenação

A ordenação da seleção pode ser estabilizada não trocando o menor elemento com o primeiro no segundo passo, mas mudando todos os elementos entre o primeiro e o menor elemento uma posição para a direita e inserindo o menor elemento no início.

Algarantia da complexidade temporal permanecerá a mesma devido a esta mudança, as mudanças adicionais levarão a uma degradação significativa do desempenho, pelo menos quando ordenamos um array.

Com uma lista ligada, cortar e colar o elemento a ser classificado poderia ser feito sem qualquer perda de performance significativa.

Paralelizabilidade de Seleção de Ordenação

Não podemos paralelizar o laço externo porque ele muda o conteúdo do array em cada iteração.

O loop interno (busca pelo menor elemento) pode ser paralelizado dividindo o array, buscando o menor elemento em cada subarranjo em paralelo, e fundindo os resultados intermediários.

Selection Sort vs. Insert Sort

Que algoritmo é mais rápido, Selection Sort, ou Insert Sort?

Vamos comparar as medidas das minhas implementações Java.

Deixar de fora o melhor caso. Com o Insertion Sort, a melhor complexidade de tempo de inserção de casos é O(n) e levou menos de um milissegundo para até 524.288 elementos. Assim, no melhor caso, o Insertion Sort é, para qualquer número de elementos, ordens de magnitude mais rápidas do que o Selection Sort.

n	Selection Sort unsorted	Insertion Sort unsorted	Selection Sort descending	Insertion Sort descending
…	…	…	…	…
16.384	27,9 ms	21,9 ms	65,6 ms	43,6 ms
32.768	108,0 ms	87,9 ms	265,4 ms	175,8 ms
65,536	434,0 ms	350,4 ms	1.052,2 ms	697,6 ms
131,072	1.729,8 ms	1.398,9 ms	4.209,9 ms	2.840,0 ms
262.144	6.913,4 ms	5.706,8 ms	16.863,7 ms	11.517,4 ms
524.288	27.649,8 ms	23.009,7 ms	67.537,8 ms	46.309,3 ms

E mais uma vez como diagrama:

Insertion Sort é, portanto, não só mais rápido do que o Selection Sort no melhor caso, mas também o caso médio e o pior.

A razão para isto é que o Inserttion Sort requer, em média, metade das comparações. Como lembrete, com o Insertion Sort, temos comparações e turnos com média de até metade dos elementos ordenados; com o Selection Sort, temos de procurar o menor elemento em todos os elementos não ordenados em cada passo.

Selection Sort tem significativamente menos operações de escrita, por isso o Selection Sort pode ser mais rápido quando as operações de escrita são caras. Este não é o caso com escritas sequenciais em arrays, pois estas são feitas principalmente no cache da CPU.

Na prática, Selection Sort é, portanto, quase nunca usado.

Summary

Selection Sort é um algoritmo de ordenação fácil de implementar, e em sua implementação típica instável, com uma média, melhor e pior complexidade de tempo de O(n²).

Selection Sort é mais lento que o Insert Sort, e é por isso que raramente é usado na prática.

Você encontrará mais algoritmos de ordenação nesta visão geral de todos os algoritmos de ordenação e suas características na primeira parte da série de artigos.

Se você gostou do artigo, sinta-se livre para compartilhá-lo usando um dos botões de compartilhamento no final. Gostaria de ser informado por e-mail quando eu publicar um novo artigo? Então use o seguinte formulário para subscrever a minha newsletter.