Quais são as frequências das notas musicais?

Na tabela de frequências abaixo, encontrará A = 440 Hz, e depois

A# = 466,16 Hz,
B = 493,88 Hz,
C = 523,25 Hz, etc.

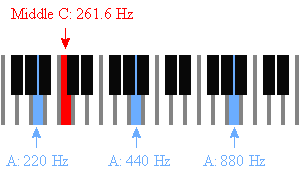
Também, pode encontrar Meio C: 261.63 Hz.

Estes são encontrados utilizando

frequência `= 440×2^(n”/”12)`

para `n = -21, -19, …., 27`

De onde veio esta fórmula?

Este problema fez-me lembrar o Compound Interest que conhecemos anteriormente em Matemática Monetária. A frequência precisa duplicar cada `12` notas (porque há `7` notas brancas e `5` notas pretas em cada oitava.)

Aqui está um gráfico dessa relação:

frequência `= 440×2^(n”/”12)`

Esta é uma curva exponencial, que encontramos anteriormente em Gráficos de Funções Exponenciais.

Afinação Igual Temperada

Um problema interessante enfrentado pelos fabricantes de instrumentos musicais durante centenas de anos. Para obter um “5º perfeito” (o intervalo entre A e E acima, digamos), precisamos tocar uma nota que tenha `1,5` vezes a frequência de A.

Num violino (ou viola ou qualquer instrumento de cordas sem freio) isto é possível, e podemos tocar um belo e perfeito E em `440 × 1,5 = 660\ “Hz”`. Mas note (da tabela de frequências acima) que um piano tocando a mesma nota tocará E `= 659,26\ “Hz”` .

Around 400 anos atrás, teclados (geralmente cravos e órgãos) eram afinados para um grupo particular de teclas, de modo que todos os instrumentos, especialmente cordas, soavam “certo” nessas teclas. O cravo soava muito bem nessas teclas, mas muito mal em outras não relacionadas (digamos B flat).

Existiam na verdade vários sistemas de afinação diferentes em uso durante o tempo de Bach, incluindo o meantone (que visava fazer com que os 3rds maiores soassem bem, mas não estava tão preocupado com a qualidade dos 5rds maiores, com o efeito de que algumas teclas não eram utilizáveis), e o Werckmeister’s 1691 afinação que permitia aos compositores criar música em qualquer tecla (com o efeito de que as várias teclas tinham uma qualidade tonal diferente).

No início do século XX, foi decidido afinar os teclados para que as notas fossem uniformemente espaçadas (como as frequências dadas na tabela apresentada acima). A isto se chama afinação temperada igual. Tal afinação era conhecida no tempo de Bach, mas rejeitada porque era considerada demasiado “suave” (todas as teclas têm a mesma qualidade de tonalidade) e não existiam ferramentas de medição de frequências que permitissem afinações exactas.

Felizmente, afinação temperada igual significa que todos os instrumentos de cordas têm de permitir as ligeiras diferenças de afinação entre instrumentos quando os teclados também estão envolvidos. As cordas são geralmente mais felizes quando tocadas apenas com outras cordas, por este motivo.