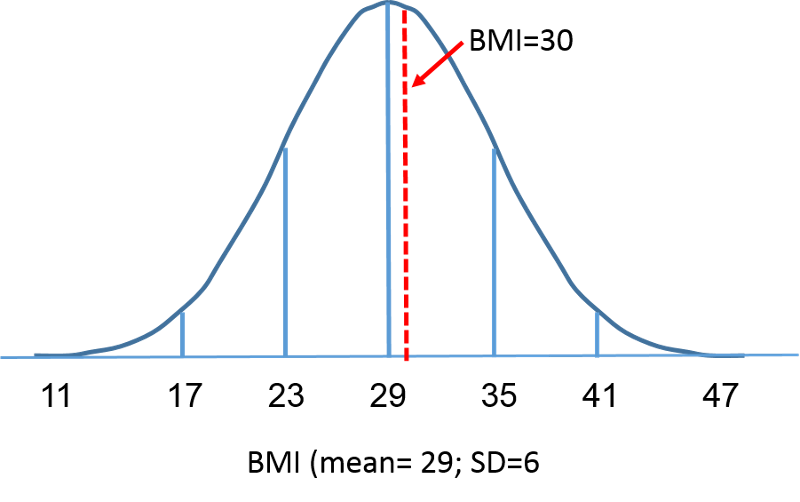
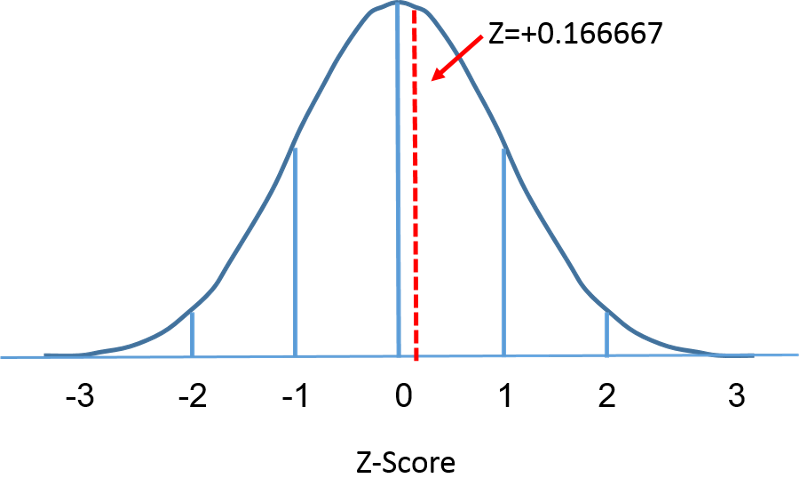
A distribuição normal padrão é uma distribuição normal com média zero e desvio padrão de 1. A distribuição normal padrão é centrada em zero e o grau em que uma determinada medida se afasta da média é dado pelo desvio padrão. Para a distribuição normal padrão, 68% das observações estão dentro de 1 desvio padrão da média; 95% estão dentro de 2 desvios padrão da média; e 99,9% estão dentro de 3 desvios padrão da média. Até este ponto, temos usado “X” para denotar a variável de interesse (por exemplo, X=IMC, X=altura, X=peso). No entanto, ao usar uma distribuição normal padrão, usaremos “Z” para nos referirmos a uma variável no contexto de uma distribuição normal padrão. Após a padronização, o IMC=30 discutido na página anterior é mostrado abaixo de 0,16667 unidades acima da média de 0 na distribuição normal padrão à direita.
 ====
====
Desde a área sob a curva padrão = 1, podemos começar a definir com mais precisão as probabilidades de observação específica. Para qualquer pontuação Z, podemos calcular a área sob a curva à esquerda dessa pontuação Z. A tabela no quadro abaixo mostra as probabilidades para a distribuição normal padrão. Examine a tabela e note que uma pontuação “Z” de 0,0 lista uma probabilidade de 0,50 ou 50%, e uma pontuação “Z” de 1, significando um desvio padrão acima da média, lista uma probabilidade de 0,8413 ou 84%. Isso porque um desvio padrão acima e abaixo da média abrange cerca de 68% da área, portanto um desvio padrão acima da média representa metade do de 34%. Assim, os 50% abaixo da média mais os 34% acima da média nos dá 84%.
Probabilidades da Distribuição Normal Padrão Z
![]()
Esta tabela é organizada para fornecer a área sob a curva à esquerda ou menos de um valor especificado ou “valor Z”. Neste caso, como a média é zero e o desvio padrão é 1, o valor Z é o número de unidades de desvio padrão longe da média, e a área é a probabilidade de observar um valor menor do que esse valor Z em particular. Observe também que a tabela mostra probabilidades a duas casas decimais de Z. As unidades decimais e a primeira casa decimal são mostradas na coluna da esquerda, e a segunda casa decimal é mostrada na linha superior.
Mas voltemos à questão sobre a probabilidade de o IMC ser inferior a 30, ou seja, P(X<30). Podemos responder a esta pergunta usando a distribuição normal. As figuras abaixo mostram as distribuições do IMC para homens com 60 anos de idade e a distribuição normal padrão, lado a lado.
Distribuição do IMC e Distribuição Normal Padrão
 ====
====
A área sob cada curva é uma, mas a escala do eixo X é diferente. Note, contudo, que as áreas à esquerda da linha tracejada são as mesmas. A distribuição do IMC varia de 11 a 47, enquanto que a distribuição normal padronizada, Z, varia de -3 a 3. Queremos calcular P(X <30). Para isso podemos determinar o valor Z que corresponde a X = 30 e depois usar a tabela de distribuição normal padronizada acima para encontrar a probabilidade ou área sob a curva. A seguinte fórmula converte um valor X em um escore Z, também chamado de escore padronizado:

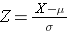
onde μ é a média e σ é o desvio padrão da variável X.
Para calcular P(X < 30) convertemos o X=30 para a sua pontuação Z correspondente (isto é chamado de padronização):

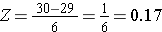
Thus, P(X < 30) = P(Z < 0,17). Podemos então procurar a probabilidade correspondente para esta pontuação Z na tabela de distribuição normal padrão, que mostra que P(X < 30) = P(Z < 0,17) = 0,5675. Assim, a probabilidade de um homem de 60 anos ter IMC inferior a 30 é 56,75%.
Outro Exemplo
Usando a mesma distribuição para o IMC, qual é a probabilidade de um homem de 60 anos ter IMC superior a 35? Em outras palavras, o que é P(X > 35)? Novamente padronizamos:

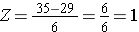
Vamos agora para a tabela de distribuição normal para procurar P(Z>1) e para Z=1,00 encontramos que P(Z<1,00) = 0,8413. Note, porém, que a tabela sempre dá a probabilidade de que Z seja menor que o valor especificado, ou seja, nos dá P(Z<1)=0,8413.
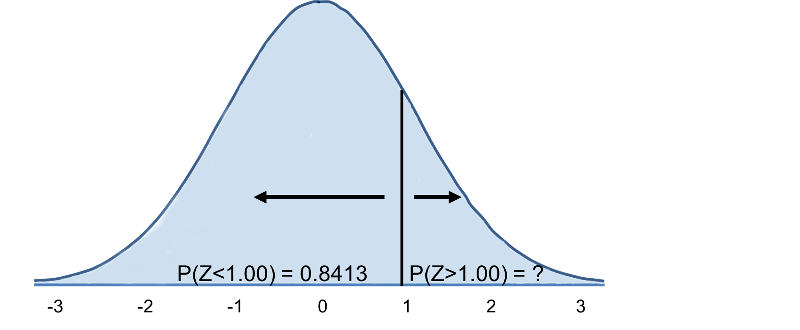
Então, P(Z>1)=1-0,8413=0,1587. Interpretação: Quase 16% dos homens com 60 anos têm IMC acima de 35,
Calculadora de Probabilidade Normal
![]()
![]()
Z-Scores com R
Como alternativa à procura de probabilidades normais na tabela ou usando Excel, podemos usar R para computar as probabilidades. Por exemplo,
> pnorm(0)
A Z-score de 0 (a média de qualquer distribuição) tem 50% da área à esquerda. Qual é a probabilidade de um homem de 60 anos na população acima ter um IMC inferior a 29 (a média)? O Z-score seria 0, e pnorm(0)=0,5 ou 50%.
Qual a probabilidade de um homem de 60 anos ter um IMC inferior a 30? A pontuação Z foi 0,16667.
> pnorm(0,16667)
Então, a probabilidade é 56,6%.
Qual é a probabilidade de um homem de 60 anos ter um IMC maior que 35?
35-29=6, o que é um desvio padrão acima da média. Assim podemos calcular a área à esquerda
> pnorm(1)
e depois subtrair o resultado de 1,0,
1-0,8413447= 0,1586553
Então a probabilidade de um homem de 60 anos ter um IMC superior a 35 é de 15,8%.
Or, podemos usar R para calcular tudo num único passo:
> 1-pnorm(1)
Probabilidade para um intervalo de valores

Qual é a probabilidade de um homem de 60 anos ter um IMC entre 30 e 35? Note que isto é o mesmo que perguntar qual a proporção de homens com 60 anos de idade que tem IMC entre 30 e 35. Especificamente, nós queremos P(30 < X < 35)? Calculámos anteriormente P(30<X) e P(X<35); como podem estes dois resultados ser utilizados para calcular a probabilidade de o IMC estar entre os 30 e os 35? Tente formular e responder por si mesmo antes de olhar para a explicação abaixo.
Resposta