Biografia
Johannes Kepler é agora lembrado principalmente por descobrir as três leis do movimento planetário que levam seu nome publicado em 1609 e 1619). Ele também fez um importante trabalho em ótica (1604, 1611), descobriu dois novos poliedros regulares (1619), deu o primeiro tratamento matemático de empacotamento próximo de esferas iguais (levando a uma explicação da forma das células de um favo de mel, 1611), deu a primeira prova de como os logaritmos funcionavam (1624), e concebeu um método para encontrar os volumes de sólidos de revolução que (com retrospectiva!) podem ser vistos como contribuindo para o desenvolvimento do cálculo (1615, 1616). Além disso, ele calculou as tabelas astronômicas mais exatas até então conhecidas, cuja precisão contínua fez muito para estabelecer a verdade da astronomia heliocêntrica (Rudolphine Tables, Ulm, 1627).
Uma grande quantidade da correspondência de Kepler sobrevive. Muitas de suas cartas são quase o equivalente a um artigo científico (ainda não havia nenhuma revista científica), e os correspondentes parecem tê-las guardado porque eram interessantes. Em consequência, sabemos muito sobre a vida de Kepler, e até sobre o seu carácter. É em parte devido a isso que Kepler teve algo da carreira de personagem mais ou menos ficcional (ver nota historiográfica abaixo).
Criança
Kepler nasceu na pequena cidade de Weil der Stadt na Suábia e se mudou para a vizinha Leonberg com seus pais em 1576. Seu pai era um soldado mercenário e sua mãe a filha de um estalajadeiro. Johannes foi o primeiro filho deles. Seu pai saiu de casa pela última vez quando Johannes tinha cinco anos, e acredita-se que tenha morrido na guerra na Holanda. Quando criança, Kepler viveu com sua mãe na estalagem de seu avô. Ele nos diz que costumava ajudar servindo na pousada. Imagina-se que os clientes eram por vezes confundidos pela incomum competência aritmética da criança.
A educação precoce de Kepler foi numa escola local e depois num seminário próximo, do qual, com a intenção de ser ordenado, continuou a inscrever-se na Universidade de Tübingen, então (como agora) um baluarte da ortodoxia luterana.
As opiniões de Kepler
Durante a sua vida, Kepler foi um homem profundamente religioso. Todos os seus escritos contêm numerosas referências a Deus, e ele via a sua obra como um cumprimento do seu dever cristão de compreender as obras de Deus. O ser humano, como Kepler acreditava, feito à imagem de Deus, era claramente capaz de compreender o Universo que Ele tinha criado. Além disso, Kepler estava convencido que Deus tinha feito o Universo de acordo com um plano matemático (uma crença encontrada nas obras de Platão e associada a Pitágoras). Como era geralmente aceite na altura que a matemática fornecia um método seguro para chegar a verdades sobre o mundo (as noções e postulados comuns de Euclides sendo considerados como realmente verdadeiros), temos aqui uma estratégia para compreender o Universo. Como alguns autores deram a Kepler um nome para irracionalidade, vale a pena notar que esta epistemologia bastante esperançosa está muito longe da convicção do místico de que as coisas só podem ser compreendidas de uma forma imprecisa, que se baseia em percepções que não estão sujeitas à razão. Kepler de fato agradece repetidamente a Deus por conceder-lhe insights, mas os insights são apresentados como racionais.
A educação universitária
Neste momento, era comum que todos os estudantes de uma universidade freqüentassem cursos sobre “matemática”. Em princípio, isto incluía as quatro ciências matemáticas: aritmética, geometria, astronomia e música. Parece, no entanto, que o que era ensinado dependia da universidade em particular. Em Tübingen Kepler foi ensinado astronomia por um dos principais astrônomos da época, Michael Mästlin (1550 – 1631). A astronomia do currículo era, naturalmente, astronomia geocêntrica, que é a versão atual do sistema Ptolemaic, no qual todos os sete planetas – Lua, Mercúrio, Vênus, Sol, Marte, Júpiter e Saturno – se moviam em torno da Terra, suas posições contra as estrelas fixas sendo calculadas através da combinação de movimentos circulares. Este sistema estava mais ou menos de acordo com as noções correntes (aristotélicas) da física, embora houvesse certas dificuldades, tais como se se poderia considerar como ‘uniforme’ (e portanto aceitável como obviamente eterno) um movimento circular que não era uniforme sobre o seu próprio centro, mas sobre outro ponto (chamado de ‘equânime’). No entanto, parece que em geral os astrônomos (que se viam como ‘matemáticos’) se contentavam em continuar a calcular as posições dos planetas e deixar aos filósofos naturais a preocupação de se os modelos matemáticos correspondiam aos mecanismos físicos. Kepler não tomou essa atitude. Seu primeiro trabalho publicado (1596) propõe considerar os caminhos reais dos planetas, não os círculos usados para construí-los.
Em Tübingen, Kepler estudou não só matemática, mas também grego e hebraico (ambos necessários para a leitura das escrituras em suas línguas originais). O ensino era em latim. No final de seu primeiro ano Kepler teve ‘A’s para tudo, exceto matemática. Provavelmente Mästlin estava tentando dizer-lhe que poderia fazer melhor, porque Kepler era de fato um dos alunos selecionados para quem ele escolheu ensinar astronomia mais avançada, introduzindo-os ao novo sistema cosmológico heliocêntrico de Copérnico. Foi de Mästlin que Kepler aprendeu que o prefácio de Sobre as revoluções, explicando que isso era “apenas matemática”, não foi de Copérnico. Kepler parece ter aceite quase instantaneamente que o sistema de Copérnico era fisicamente verdadeiro; suas razões para aceitá-lo serão discutidas em conexão com seu primeiro modelo cosmológico (ver abaixo).
Parece que mesmo nos dias de estudante de Kepler havia indicações de que suas crenças religiosas não estavam inteiramente de acordo com o ortodoxo luteranismo atual em Tübingen e formulado no Confessio Augustana Ⓣ. Os problemas de Kepler com essa ortodoxia protestante diziam respeito à suposta relação entre matéria e ‘espírito’ (uma entidade não-material) na doutrina da Eucaristia. Isso se relaciona com a astronomia de Kepler na medida em que ele aparentemente encontrou dificuldades intelectuais um pouco semelhantes para explicar como a ‘força’ do Sol poderia afetar os planetas. Em seus escritos, Kepler é dado a colocar suas opiniões na linha – o que é muito conveniente para os historiadores. Na vida real, parece provável que uma tendência semelhante para a abertura tenha levado as autoridades de Tübingen a entreter dúvidas bem fundamentadas sobre a sua ortodoxia religiosa. Isto pode explicar porque Mästlin persuadiu Kepler a abandonar os planos para a ordenação e, em vez disso, assumir um cargo de professor de matemática em Graz. A intolerância religiosa foi intensificada nos anos seguintes. Kepler foi excomungado em 1612. Isso lhe causou muita dor, mas apesar de sua (até então) posição social relativamente alta, como matemático imperial, ele nunca conseguiu que a proibição fosse levantada.
O primeiro modelo cosmológico de Kepler (1596)
Em vez dos sete planetas da astronomia geocêntrica padrão, o sistema copernicano tinha apenas seis, tendo a Lua se tornado um corpo do tipo anteriormente desconhecido para a astronomia, que Kepler foi mais tarde para chamar de ‘satélite’ (um nome que ele cunhou em 1610 para descrever as luas que Galileu tinha descoberto estavam orbitando Júpiter, literalmente significando ‘atendente’). Por que seis planetas?
Mais ainda, na astronomia geocêntrica não havia como usar observações para encontrar os tamanhos relativos dos orbes planetários; eles foram simplesmente assumidos como estando em contato. Isto parecia não requerer nenhuma explicação, uma vez que se encaixava bem na crença dos filósofos naturais de que todo o sistema estava virado a partir do movimento da esfera mais externa, uma (ou talvez duas) para além da esfera das estrelas “fixas” (aquelas cujo padrão fazia as constelações), para além da esfera de Saturno. No sistema copernicano, o fato de que a componente anual de cada movimento planetário era um reflexo do movimento anual da Terra permitiu que se utilizassem observações para calcular o tamanho do caminho de cada planeta, e verificou-se que existiam enormes espaços entre os planetas. Porque é que estes espaços particulares?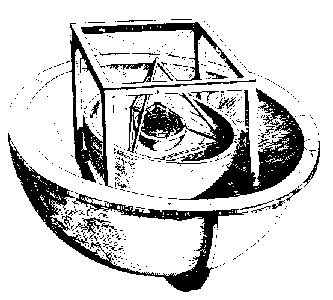
Kepler responde a estas questões, descritas no seu Mysterium cosmographicum Ⓣ, Tübingen, 1596, parece bizarro aos leitores do século XX (ver a figura à direita). Ele sugeriu que se uma esfera fosse atraída para tocar o interior do caminho de Saturno, e um cubo fosse inscrito na esfera, então a esfera inscrita nesse cubo seria a esfera que circunscreveria o caminho de Júpiter. Então, se um tetraedro regular fosse desenhado na esfera, inscrevendo o caminho de Júpiter, a inspiração do tetraedro seria a esfera circunscrevendo o caminho de Marte, e assim para dentro, colocando o dodecaedro regular entre Marte e Terra, o icosaedro regular entre Terra e Vênus, e o octaedro regular entre Vênus e Mercúrio. Isto explica perfeitamente o número de planetas: existem apenas cinco sólidos convexos regulares (como está provado nos Elementos de Euclides , Livro 13). Também dá um ajuste convincente com os tamanhos dos caminhos como deduzido por Copérnico, sendo o maior erro inferior a 10% (o que é espetacularmente bom para um modelo cosmológico ainda hoje). Kepler não se expressou em termos de erros percentuais, e o seu é de fato o primeiro modelo cosmológico matemático, mas é fácil ver porque ele acreditava que as evidências observacionais apoiavam a sua teoria.
Kepler viu a sua teoria cosmológica como evidência para a teoria de Copérnico. Antes de apresentar sua própria teoria, ele deu argumentos para estabelecer a plausibilidade da própria teoria de Copérnico. Kepler afirma que suas vantagens sobre a teoria geocêntrica estão em seu maior poder explicativo. Por exemplo, a teoria de Copérnico pode explicar porque Vênus e Mercúrio nunca são vistos muito longe do Sol (eles ficam entre a Terra e o Sol) enquanto que na teoria geocêntrica não há explicação para este fato. Kepler lista nove dessas questões no primeiro capítulo do Mysterium cosmographicum Ⓣ.
Kepler realizou este trabalho enquanto ensinava em Graz, mas o livro foi visto através da imprensa em Tübingen por Mästlin. O acordo com os valores deduzidos da observação não era exato, e Kepler esperava que melhores observações melhorassem o acordo, então ele enviou uma cópia do Mysterium cosmographicum para um dos maiores astrônomos observacionais da época, Tycho Brahe (1546 – 1601). Tycho, então trabalhando em Praga (naquela época a capital do Santo Império Romano), de fato já tinha escrito para Mästlin em busca de um assistente matemático. Kepler conseguiu o emprego.
A ‘Guerra com Marte’
Naturalmente, as prioridades de Tycho não eram as mesmas de Kepler, e Kepler logo se viu trabalhando no problema intratável da órbita de Marte. Ele continuou a trabalhar nisso após a morte de Tycho (em 1601) e Kepler o sucedeu como Matemático Imperial. Convencionalmente, as órbitas eram compostas por círculos, e eram necessários poucos valores observacionais para fixar os raios relativos e as posições dos círculos. Tycho tinha feito um grande número de observações e Kepler estava determinado a fazer o melhor uso possível das mesmas. Essencialmente, ele tinha tantas observações disponíveis que, uma vez construída uma possível órbita, foi capaz de verificá-la em relação a outras observações até que se chegasse a um acordo satisfatório. Kepler concluiu que a órbita de Marte era uma elipse com o Sol em um de seus focos (um resultado que quando estendido a todos os planetas é agora chamado de “Primeira Lei de Kepler”), e que uma linha unindo o planeta ao Sol varreu áreas iguais em tempos iguais como o planeta descreveu sua órbita (“Segunda Lei de Kepler”), ou seja, a área é usada como uma medida de tempo. Depois deste trabalho ter sido publicado em Astronomia nova, … Ⓣ, Heidelberg, 1609, Kepler encontrou órbitas para os outros planetas, estabelecendo assim que as duas leis também se aplicavam a eles. Ambas as leis relacionam o movimento do planeta com o Sol; o copernicanismo de Kepler foi crucial para o seu raciocínio e para as suas deduções.
O verdadeiro processo de cálculo para Marte foi imensamente laborioso – existem quase mil folhas de fólio de aritmética sobreviventes – e o próprio Kepler refere-se a este trabalho como “a minha guerra com Marte”, mas o resultado foi uma órbita que concorda com os resultados modernos de forma tão exacta que a comparação tem de ter em conta as mudanças seculares na órbita desde os tempos de Kepler.
Observational error
Foi crucial para o método de Kepler verificar possíveis órbitas contra observações de que ele tem uma idéia do que deve ser aceito como acordo adequado. Daí surge o primeiro uso explícito do conceito de erro observacional. Kepler pode ter ficado a dever esta noção pelo menos em parte a Tycho, que fez verificações detalhadas sobre o desempenho dos seus instrumentos (ver a biografia de Brahe).
Optics, e a Nova Estrela de 1604
O trabalho em Marte foi essencialmente concluído em 1605, mas houve atrasos na publicação do livro. Entretanto, em resposta às preocupações sobre os diferentes diâmetros aparentes da Lua quando observada directamente e quando observada com uma câmara obscura, Kepler fez algum trabalho sobre óptica, e chegou à primeira teoria matemática correcta da câmara obscura e à primeira explicação correcta do funcionamento do olho humano, com uma imagem de cabeça para baixo formada na retina. Estes resultados foram publicados em Ad Vitellionem paralipomena, quibus astronomiae pars optica traditur Ⓣ, Frankfurt, 1604. Ele também escreveu sobre a Nova Estrela de 1604, agora normalmente chamada ‘a supernova de Kepler’, rejeitando inúmeras explicações, e observando em certo ponto que, é claro, esta estrela poderia ser apenas uma criação especial ‘mas antes de chegarmos a mim acho que devemos tentar tudo o resto’ De stella nova Ⓣ, Praga, 1606, Capítulo 22, KGW 1, p. 257, linha 23.
Seguindo o uso do telescópio por Galileu na descoberta das luas de Júpiter, publicado no seu Sidereal Messenger (Veneza, 1610), para o qual Kepler tinha escrito uma resposta entusiasta (1610), Kepler escreveu um estudo sobre as propriedades das lentes (o primeiro trabalho sobre óptica) no qual apresentou um novo desenho do telescópio, usando duas lentes convexas (Dioptrice, Praga, 1611). Este desenho, no qual a imagem final é invertida, teve tanto sucesso que agora é normalmente conhecido não como um telescópio Kepler, mas simplesmente como o telescópio astronómico.
Leaving Prague for Linz
Kepler’s years in Prague were relatively peaceful, and scientifically extremely productive. Na verdade, mesmo quando as coisas corriam mal, ele parece nunca ter permitido que circunstâncias externas o impedissem de continuar com o seu trabalho. As coisas começaram a correr muito mal no final de 1611. Primeiro, seu filho de sete anos de idade morreu. Kepler escreveu a um amigo que essa morte foi particularmente difícil de suportar porque a criança o lembrava tanto de si mesmo naquela idade. Depois a mulher de Kepler morreu. Então o imperador Rudolf, cuja saúde estava falhando, foi obrigado a abdicar a favor de seu irmão Matthias, que, como Rudolf, era católico, mas (ao contrário de Rudolf) não acreditava na tolerância com os protestantes. Kepler teve que deixar Praga. Antes de partir, ele fez com que o corpo de sua esposa fosse transferido para o túmulo do filho, e escreveu um epitáfio latino para eles. Ele e seus filhos restantes mudaram-se para Linz (agora na Áustria).
Casamento e barris de vinho
Kepler parece ter casado com sua primeira esposa, Barbara, por amor (embora o casamento tenha sido arranjado através de um corretor). O segundo casamento, em 1613, foi uma questão de necessidade prática; ele precisava de alguém que cuidasse dos filhos. A nova esposa de Kepler, Susanna, teve um curso intensivo na personagem de Kepler: a carta dedicatória ao livro resultante explica que nas celebrações do casamento ele notou que os volumes de barris de vinho foram estimados por meio de uma vara que escorregou diagonalmente pelo buraco do bung-hole, e ele começou a se perguntar como isso poderia funcionar. O resultado foi um estudo dos volumes de sólidos da revolução Nova stereometria doliorum … Ⓣ, Linz, 1615, em que Kepler, baseando-se na obra de Arquimedes, usou uma resolução em ‘indivisíveis’. Este método foi mais tarde desenvolvido por Bonaventura Cavalieri (c. 1598 – 1647) e faz parte da ancestralidade do cálculo infinitesimal.
The Harmony of the World
Kepler’s principal tarefa como Matemático Imperial era escrever tabelas astronômicas, baseadas nas observações de Tycho, mas o que ele realmente queria fazer era escrever A Harmonia do Mundo, planejada desde 1599 como um desenvolvimento do seu Mistério do Cosmos. Este segundo trabalho sobre cosmologia (Harmonices mundi libri V Ⓣ, Linz, 1619) apresenta um modelo matemático mais elaborado do que o anterior, embora os poliedros ainda estejam lá. A matemática deste trabalho inclui o primeiro tratamento sistemático das tesselações, uma prova de que existem apenas treze poliedros convexos uniformes (os sólidos arquimedesanos) e o primeiro relato de dois poliedros regulares não convexos (todos no Livro 2). A Harmonia do Mundo também contém o que agora é conhecido como “Terceira Lei de Kepler”, que para quaisquer dois planetas a proporção dos quadrados dos seus períodos será a mesma que a proporção dos cubos dos raios médios das suas órbitas. Desde o primeiro, Kepler procurou uma regra que relacionasse os tamanhos das órbitas com os períodos, mas não havia uma série lenta de passos em direcção a esta lei como havia havido em relação aos outros dois. Na verdade, embora a Terceira Lei desempenhe um papel importante em algumas das secções finais da versão impressa da Harmonia do Mundo, ela só foi realmente descoberta quando a obra foi impressa. Kepler fez revisões de última hora. Ele mesmo conta a história de um eventual sucesso:
…e se quiser o momento exacto no tempo, foi concebido mentalmente a 8 de Março deste ano mil seiscentos e dezoito, mas submetido a cálculo de uma forma azarada, e portanto rejeitado como falso, e finalmente voltando no dia 15 de Maio e adoptando uma nova linha de ataque, invadiu a escuridão da minha mente. Tão forte foi o apoio da combinação do meu trabalho de dezessete anos sobre as observações de Brahe e o presente estudo, que conspiraram juntos, que a princípio eu acreditava estar sonhando, e assumindo minha conclusão entre minhas premissas básicas. Mas é absolutamente certo e exato que “a proporção entre os tempos periódicos de quaisquer dois planetas é precisamente a proporção sesquialterada de suas distâncias médias…”
(Harmonice mundi Book 5, Capítulo 3, trans. Aiton, Duncan e Field, p. 411).
Witchcraft trial
Enquanto Kepler estava trabalhando em sua Harmonia do Mundo, sua mãe foi acusada de bruxaria. Ele contou com a ajuda da faculdade de direito de Tübingen. Katharina Kepler foi eventualmente libertada, pelo menos em parte como resultado de objecções técnicas decorrentes da falha das autoridades em seguir os procedimentos legais correctos no uso da tortura. Os documentos sobreviventes são arrepiantes. No entanto, Kepler continuou a trabalhar. No ônibus, em sua viagem a Württemberg para defender sua mãe, ele leu um trabalho sobre teoria musical de Vincenzo Galilei (c.1520 – 1591, pai de Galileu), ao qual há numerosas referências em A Harmonia do Mundo.
Tabelas Astronômicas
Calculando tabelas, o negócio normal para um astrônomo, sempre envolvia aritmética pesada. Kepler ficou, portanto, encantado quando, em 1616, encontrou o trabalho de Napier sobre logaritmos (publicado em 1614). Entretanto, Mästlin prontamente lhe disse primeiro que era inconveniente para um matemático sério alegrar-se com uma simples ajuda ao cálculo e segundo que não era prudente confiar nos logaritmos porque ninguém entendia como eles funcionavam. (Comentários semelhantes foram feitos sobre computadores no início dos anos 60.) A resposta de Kepler à segunda objeção foi publicar uma prova de como os logaritmos funcionavam, com base em uma fonte impecavelmente respeitável: Euclid’s Elements Book 5. Kepler calculou tabelas de logaritmos de oito dígitos, que foram publicadas com as Tabelas de Rudolphine (Ulm, 1628). As tabelas astronômicas utilizaram não apenas as observações de Tycho, mas também as duas primeiras leis de Kepler. Todas as tabelas astronômicas que faziam uso de novas observações foram precisas durante os primeiros anos após a publicação. O que foi notável sobre as Tabelas de Rudolphine foi que elas provaram ser precisas durante décadas. E como os anos se passaram, a precisão contínua das tabelas foi, naturalmente, vista como um argumento para a exatidão das leis de Kepler e, portanto, para a exatidão da astronomia heliocêntrica. O cumprimento de Kepler da sua aborrecida tarefa oficial como Matemático Imperial levou à realização do seu mais querido desejo, de ajudar a estabelecer o copernicanismo.
Wallenstein
Por ocasião da publicação das Tabelas Rudolphine Kepler já não trabalhava mais para o Imperador (ele havia deixado Linz em 1626), mas para Albrecht von Wallenstein (1583 – 1632), um dos poucos líderes militares de sucesso na Guerra dos Trinta Anos (1618 – 1648).
Wallenstein, assim como o imperador Rudolf, esperava que Kepler lhe desse conselhos baseados na astrologia. Kepler naturalmente teve que obedecer, mas repetidamente aponta que ele não acredita que previsões precisas possam ser feitas. Como a maioria das pessoas da época, Kepler aceitou o princípio da astrologia, que os corpos celestes poderiam influenciar o que aconteceu na Terra (os exemplos mais claros sendo o Sol causando as estações e a Lua as marés), mas como copernicano ele não acreditava na realidade física das constelações. A sua astrologia baseava-se apenas nos ângulos entre as posições dos corpos celestiais (“aspectos astrológicos”). Ele expressa total desprezo pelos complicados sistemas da astrologia convencional.
Morte
Kepler morreu em Regensburg, após uma curta doença. Ele estava a caminho da cidade para recolher algum dinheiro que lhe era devido em ligação com as Mesas de Rudolphine. Ele foi enterrado na igreja local, mas isto foi destruído durante a Guerra dos Trinta Anos e nada resta do túmulo.
Nota historiográfica
Muito foi feito às vezes de elementos supostamente não racionais na atividade científica de Kepler. Os astrólogos crentes afirmam frequentemente que o seu trabalho proporciona um antecedente cientificamente respeitável ao seu próprio trabalho. Nos seus influentes Sleepwalkers o falecido Arthur Koestler transformou a batalha de Kepler com Marte num argumento para a inerente irracionalidade da ciência moderna. Tem havido muitos seguidores tácitos destas duas persuasões. Ambas são, no entanto, baseadas na leitura muito parcial do trabalho de Kepler. Em particular, Koestler parece não ter tido a perícia matemática para compreender os procedimentos de Kepler. Um estudo mais próximo mostra que Koestler estava simplesmente enganado na sua avaliação.
O elemento verdadeiramente importante não racional no trabalho de Kepler é o seu cristianismo. O uso extensivo e bem sucedido da matemática por Kepler faz seu trabalho parecer ‘moderno’, mas na verdade estamos lidando com um Filósofo Natural Cristão, para quem a compreensão da natureza do Universo incluía a compreensão da natureza de seu Criador.