Escrevendo equações lineares usando a forma de intercepção da inclinação

Uma equação na forma de intercepção da inclinação é escrita como

$$y=mx+b$$

Onde m é a inclinação da linha e b é o intercepção y. Você pode usar esta equação para escrever uma equação se você souber a inclinação e o y-intercepção.

Exemplo

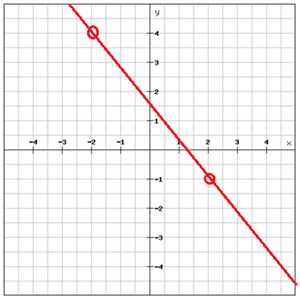
Encontrar a equação da linha

>

Escolha dois pontos que estão na linha

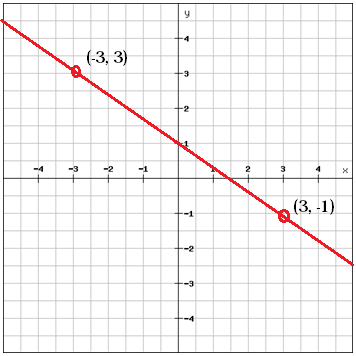
Calcular a inclinação entre os dois pontos

$$m=\frac{y_{2}}, -y_{1}{x_{2}}{x_{2}}, -x_{1}=frac{{1}=esquerda (-1 {direita )-3}{3-esquerda ( -3 {direita )}=frac{-4}{6}=frac{-2}{3}$$

Nós podemos encontrar o valor b, o intercepção y, olhando para o gráfico

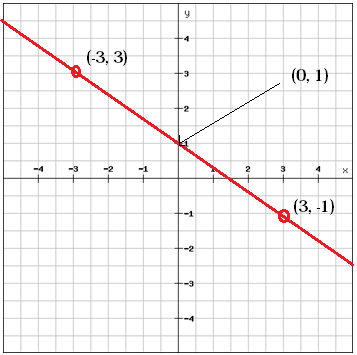
b = 1

Temos um valor para m e um valor para b. Isto nos dá a função linear

$$y=-\frac{2}{3}x+1$$

> Em muitos casos o valor de b não é tão facilmente lido. Nesses casos, ou se você não tiver certeza se a linha realmente cruza o eixo y neste ponto em particular, você pode calcular b resolvendo a equação para b e depois substituindo x e y por um dos seus dois pontos.

Podemos usar o exemplo acima para ilustrar isso. Nós temos os dois pontos (-3, 3) e (3, -1). A partir destes dois pontos calculamos a inclinação

$$m=-\frac{2}{3}$$$

Isto dá-nos a equação

$$y=-\frac{2}{3}x+b$$

A partir disto podemos resolver a equação para b

$$b=y+\frac{2}{3}x$$

E se colocarmos os valores do nosso primeiro ponto (-3, 3) nós recebemos

$$b=3+\frac{2}{3}{3}cdot \i>esquerda ( -3 \i>direita )=3+esquerda ( -2 \i>direita )=1$$$

Se colocarmos este valor para b na equação, recebemos

$$y=-\frac{2}{3}x+1$$

que é a mesma equação que obtivemos quando lemos o y-intercepção do gráfico.

Para resumir como escrever uma equação linear usando a forma de intercepção da inclinação você

1. Identificar a inclinação, m. Isto pode ser feito calculando a inclinação entre dois pontos conhecidos da linha usando a fórmula da inclinação.
2. Localizar o intercepção y. Isto pode ser feito substituindo a inclinação e as coordenadas de um ponto (x, y) na linha da fórmula da inclinação e depois resolver para b.

Após ter ambos m e b pode simplesmente colocá-los na equação na sua respectiva posição.

Lição de vídeo

Lição de vídeo

Lição de vídeo